Виды отклонений. Общий случай

Первую группу составляют меры, близкие к мерам отклонения (1.41) - (1.43); каждый элемент множества В _аучтен с весом, равным p_а(b_i), причем для i = 1, 2,..., п выполняется условие . Аналогичным образом, для r₁ (1.41) средневзвешенное отклонение элементов множества В _а от точки b^* составляет

d_ср = (1.47а)

либо

. (1.48б)

Среднеквадратическое отклонение (1.42) называется стандартным отклонением распределения вероятности. Оно рассчитывается по формуле

(1.49a)

либо

, (1.49б)

где значение ` b = b ₂^* в соответствии с решением D ₂.

Для распределений р_а(b), симметричных относительно точки b^*, выполняется условие b ₁^* = b ₂^* = b^*. Аналогично для отклонения r₃ (1.43) определяются при b = b ₂^*, q = 2, 3, 4,.... центральные моменты порядка q вероятностного распределения:

m_q = (1.50а)

или

m_q = . (1.50б)

Интервальные меры

Первое условие. Вторую группу мер неоднозначности отображения а®В образуют интервальные меры, близкие к мере Лебега, после выделения определенного подмножества из множества В_а посредством дополнительного условия. Можно поставить условие, чтобы вероятность реализации элемента b_i была соответственно велика, например:

p_а(b_i)>p _min > 0. (1.51)

 

Рис. 1.7. Мера неоднозначности образа при р_а(b)>р _min:

а - графическая интерпретация меры;

б - случай, когда мера не вполне характеризует неоднозначность образа

 

Условие (1.51) выполняется для множества

В_р={bÎВ_а:р(b)> p _min }, (1.52)

как это иллюстрирует рис. 1.7,а. Множество В_р можно охарактеризовать мерой Лебега (1.46), и тогда

m(В_р) = m_н+m_в = 2m, (1.53)

где m = (m_в+m_н)/2.

Достоинством условия (1.51) (p > p _min) является ограничение множества образов тогда, когда множество В_а теоретически бесконечно (например, множество с нормальным распределением). Для нормального распределения выбор p _min из условия

p _min/ p _max = 0. 1 приводит к m(В_р) = 2×2,15s = 4,30s, (1.54)

а из условия

p _min/ p _max = 0.01 – к m(В_р) = 2×3,04s = 6,08s. (1.55)

Мера Лебега множества В_р кратна стандартному отклонению s. Как показывает рис. 1.7,б, такая мера неудобна для некоторых распределений, например для бимодальных и несвязанных, поскольку приводит к разрыву функции p (b) – второе условие.

Второе условие. Множество В_а можно также ограничить условием, чтобы окрестность точки b^* содержала некоторую a - часть элементов всего множества В_а. Путем подбора значений e_н, e_в>0, соответствующих условию

<1 (1.56)

или двум условиям

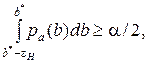
, (1.57)

получается множество В_aÎ В_а. Мера Лебега множества B_a составляет

m(В_a) = e_н+e_в=2e>0, (1.58)

где e = (e_н+e_в)/2.

В этом случае интервал 2e называется доверительным интервалом, а a - доверительным уровнем. Графическая интерпретация доверительных интервалов показана на рис. 1.8.

Для нормального распределения интервал 2·2s содержит 95% элементов множества В_а, а интервал 2·Зs - соответственно 99,7%.

Рис. 1.8. Способы выделения множества В _a

а - из условия (1.56); б - из условия (1.57)

 

Встречается еще одна интервальная мера, а именно ширина распределения. Если нижний и верхний пределы множества В_а равны соответственно b _н и b _в, то ширина (разброс)

W = b _в - b _н > 0. (1.59)

Ширина распределения в этом случае равна значению меры Лебега для множества В_а (1.45,в).

Энтропия

Третьим видом меры неоднозначности отображения а ® В_а является энтропия (или негэнтропия), выражаемая формулой

(1.60а)

либо

Н = . (1.60б)

Интересно, что возможно НËВ, хотя энтропия выражается действительными числами. Это логарифмическая мера определенного интервала, длина которого зависит от распределения вероятности р_а(b), а также от характеристик дисперсии распределения. Для множества с равномерным распределением (1.40) энтропия описывается выражением

H = ln (b _в – b _н), (1.61)

а энтропия множества с нормальным распределением составляет

. (1.62)

Энтропия является мерой упорядочения или неопределенности, используемой в термодинамике. Наибольшую неопределенность имеет множество с равномерным распределением.

Энтропию следует рассматривать как меру, позволяющую сравнивать два множества с различными распределениями вероятностей. Если два сравниваемых множества имеют распределения одного вида (например, нормальное или равномерное), то их можно сравнить через отношение параметров их функции вероятности.

Два множества с распределениями разного вида с точки зрения энтропии эквивалентны, если их энтропии равны. Эквивалентность либо упорядоченность множества с позиций энтропии не имеет иного значения.

 

Итог

До сих пор говорилось об одноразовом акте познания состояния а данной характеристики. Образом состояния а является множество значений В_а={b}, а также множество вероятностей р_а(b), соответствующих условию (1.25) реализации значения b; при этом в качестве наилучшего образа выбирается, по одному из возможных решающих правил (1.27), значение b^*. Неоднозначность отображения состояния а в значение b^* характеризует множество значений

{b}¹ b^*, (1.63)

находящихся в окрестности точки b^*, либо, в соответствии с (1.36), множество состояний

А^*¹а. (1.64)

Исследование состояний материи и энергии ведется путем многократного осуществления познавательных актов. Отыскивается либо множество образов (в предположении, что данная характеристика сохраняет свое состояние а), либо множество прообразов состояний а, интерпретированных как различные множества {А^*}. Следовательно, существует возможность сравнения образов между собой в предположении, что состояние данной характеристики не меняется. Сравнить требуется значения b^*, а также распределения вероятности р_а(b) либо иные меры неоднозначности образов. Сложность таких сравнений, пожалуй, не вызывает сомнений. Этой задачей занимается математическая статистика.

 

Контрольные вопросы к разделу 1

1. Какие формы познания существуют и чем они отличаются?

2. Назовите составляющие структуры познаваемого мира и его абстрактного отображения.

3. Что такое функция прямого и функция обратного отображения?

4. Какие основные соотношения характеристик физических величин вы знаете?

5. Чем отличаются основные и производные величины? Приведите примеры таких величин.

6. Чем отличаются эмпирические шкалы физических величин от метрических?

7. Какие виды шкал вы знаете? В чем их различие?

8. Какой физической величиной определяется цвет?

9. Как задается метрическая шкала цвета? Опишите метод смешения цветов.

10. Для чего была введена характеристика цвета «яркость»?

11. В чем отличие проблемы расширения метрической системы в областях естественного и гуманитарного знания?

12. В чем заключается неоднозначность прямого и обратного отображения?

13. Какие правила выбора наилучшего решения вы знаете?

14. Какие способы, характеризующие неопределенность отображения, вы знаете?

15. Что такое мера множества?

16. Для чего предназначены интервальные меры?

17. Как энтропия характеризует неопределенность отображения?