Образование переходов методом диффузии

Диффузия из источника бесконечной мощности (неограниченного поверхностного источника) вглубь полупроводника. В данном случае распределение концентрации примеси в полупроводнике в направлении оси x определяется соотношением

 

, (1.11)

 

где N ₀ – концентрация примеси в источнике диффузанта; D – коэффициент диффузии атомов примеси в полупроводнике; t – время диффузии; erfc – функция дополнения к интегралу ошибок Гаусса.

 

,

где .

Для большинства практически важных случаев величина z заключена в интервале от 2 до 3. Пример распределения акцепторной примеси в полупроводнике n-типа проводимости показан на рис. 1.

 

Рис. 1. Распределение донорной и акцепторной примесей

 

В точке x = x ₀ (глубина залегания p–n-перехода) проводимость меняет свой тип.

Для практически важного случая, когда

 

N_D << N_0A

 

можно получить

 

. (1.12)

 

Если N_D = 10¹⁴ см^-3 и N_0A = 10²⁰ см^-3, то

 

.

 

Градиент концентрации примесей при данном распределении может быть найден из выражения

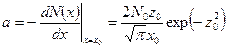[см^-4],

 

где .

Диффузия из источника ограниченной мощности. В этом случае концентрация диффузанта в источнике уменьшается с течением времени по закону Гаусса:

 

, (1.13)

 

где h – толщина слоя, из которого идет диффузия.

В приближении, когда , можно использовать распределение, значительно упрощающее расчеты

 

, (1.14)

 

где α – показатель экспоненты, аппроксимирующей распределение атомов примесей диффузанта, [см^-1].

Распределение акцепторной примеси для рассмотренных видов диффузии в полупроводнике n-типа проводимости показано на рис. 2.

Коэффициент диффузии определяется свойствами полупроводника, диффузанта и температурой:

 

 

Рис. 2. Распределение примесей при образовании p–n-переходов методом диффузии

 

. (1.15)

 

Константу D ₀ можно определить из уравнения Лангмюра – Дэшмена:

 

, (1.16)

 

где a – постоянная решетки; E – энергия активации; N_A – число Авогадро; h – постоянная Планка.

Пользуясь формулами для расчета концентраций диффузанта, следует учитывать, что вследствие существования предела растворимости диффузанта в основном веществе N ₀ не может быть выше этой предельной растворимости.

Из рис. 2 следует, что величину α можно определить из соотношения

 

[см^-1].

 

При известной величине α глубина залегания p–n-перехода определяется из условия N (x) = N_D.

Градиент концентрации примесей при данном распределении определяется как

 

[см^-4].

 

1.2.3. Расчет контактной разности потенциалов. Напомним, что электронно-дырочный переход – это контакт двух полупроводников с различным типом проводимости. Электропроводность полупроводников, обусловленная основными носителями зарядов, определяется следующими выражениями:

 

s_p=qN_Аm_p, (1.17)

s_n=qN_Dm_n, (1.18)

где s_p, s_n – электропроводность полупроводников p- и n-типов.

Удельное сопротивление полупроводника p-типа

 

r_p=(qN_Am_p)^{- 1}, (1.19)

откуда концентрация акцепторов равна

N_A=(qr_pm_p)^{- 1}. (1.20)

Аналогично концентрация доноров определяется соотношением

 

N_D=(qr_nm_n)^{- 1}. (1.21)

 

При известных значениях N_A и N_D выражение для диффузионного потенциала (контактной разности потенциалов) может быть представлено в виде

 

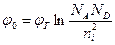. (1.22)

 

1.2.4. Расчет вольт-амперной характеристики p–n-перехода. Вольтамперная характеристика (ВАХ) идеального p–n-перехода может быть представлена в виде

 

, (1.23)

 

где I₀ – ток насыщения; U – напряжение, приложенное к переходу. Ток насыщения I₀ определяется следующим выражением:

 

[А], (1.24)

 

где S – площадь p–n-перехода.

Когда N_A >> N_D (p–n-переход несимметричный), обратный ток насыщения определяется соотношением

[А]. (1.25)

 

Когда N_D >> N_A, то

 

[А]. (1.26)

 

1.2.5. Определение дифференциального сопротивле-ния p-n-перехода. Выражение (1.23) может быть представлено в виде

 

. (1.27)

 

Дифференцируя (1.27) по напряжению можно получить

 

 

Следовательно, в общем случае дифференциальное сопротивление

 

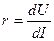=j_Т/(I₀+I),(1.28)

Если величина прямого тока существенно превышает величину тока насыщения (I»I₀), то

 

 

В этом случае

r=j_Т /I. (1.29)

 

1.2.6. Определение величины барьерной емкости p-n-перехода. Величина удельной барьерной емкости резкого p–n-перехода в общем случае рассчитывается по формуле

 

. (1.30)

 

При этом ширина обедненного слоя (ширина p–n-перехода) определяется выражением

 

, (1.31)

 

где .

Удельная барьерная емкость плавного p–n-перехода может быть определена соотношением

 

, (1.32)

 

где а – градиент концентрации примесей, [м^-4].

Ширина p–n-перехода

 

. (1.33)

 

1.2.7. Определение напряжения пробоя U_пр. При большом обратном смещении на p–n-переходе, которое создает в нем большое электрическое поле, переход «пробивается» и через него протекает большой ток. Существует три основных механизма пробоя: тепловая неустойчивость, туннельный эффект и лавинное умножение.

Тепловой пробой является основным фактором в полупроводниках с относительно малой шириной запрещенной зоны E_g, например в германии. Однако при очень низких температурах, а также при специальных мерах по ограничению тока, протекающего через p–n-переход (включение токоограничивающего резистора) или по теплоотводу (установка радиаторов охлаждения), тепловая неустойчивость становится несущественной по сравнению с другими механизмами пробоя.

Когда электрическое поле в германии или кремнии достигает величин порядка 10⁶ В/см, через p–n-переход начинают протекать токи, обусловленные туннельными переходами носителей заряда между разрешенными зонами полупроводников.

Чтобы получить такое сильное поле, толщина области пространственного заряда должна быть небольшой, следовательно, концентрации примеси в p- и n- областях должны быть достаточно высокими.

Установлено, что механизм пробоя в кремниевых и германиевых p–n-переходах является туннельным при напряжениях пробоя, меньших 4 E_g / q. В переходах с напряжением пробоя, превышающим 6 E_g / q, механизм пробоя обусловлен лавинным умножением.

Лавинное умножение, или ударная ионизация, является наиболее важным механизмом пробоя p–n-перехода. Напряжение лавинного пробоя определяет верхний предел обратного напряжения большинства диодов, коллекторного напряжения биполярных транзисторов, напряжения стока полевых транзисторов.

Напряжение лавинного пробоя p–n-перехода можно определить, зная величины максимального электрического поля и ширины области пространственного заряда.

Величина максимального значения напряженности электрического поля в p–n-переходе, сформированном на кремнии, определяется выражением

 

, (1.34)

 

где N – концентрация примеси в высокоомной области p–n-перехода измеряется в см^-3.

Если ширина области пространственного заряда p–n-перехода (W) известна, то напряжение пробоя для резкого несимметричного перехода

 

, (1.35)

 

а для плавного перехода

 

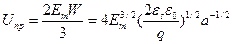. (1.36)

 

Оценка величины напряжения пробоя резкого p-n-перехода может быть сделана на основании универсального приближенного выражения, справедливого для различных полупроводников:

 

[В]. (1.37)

Для плавного перехода величину напряжения пробоя можно оценить, используя соотношение

 

[В]. (1.38)

 

В выражениях (1.35) – (1.38) размерность величины а в см^-4, а значение ширины запрещенной зоны полупроводника E_g при комнатной температуре в эВ.

Для p–n-перехода, полученного диффузионным методом, с линейным распределением примеси на одной стороне и с постоянной концентрацией примеси на другой стороне перехода напряжение пробоя принимает промежуточное значение между напряжением пробоя резкого и линейного переходов.

Для низких значений N напряжение пробоя диффузионного перехода приближается к напряжениям для резкого перехода; для высоких N напряжение близко к напряжениям для линейного перехода.

Выражения (1.34 – 1.38) получены в предположении достаточно большой толщины области пространственного заряда, чтобы существовали условия, необходимые для реализации процесса лавинного умножения носителей заряда.

 

1.2.8. Порядок построения энергетической диаграм-мы p-n-перехода. Для построения энергетической диаграммы несимметричного электронно-дырочного перехода при заданном напряжении смещения U необходимо определить следующие электрофизические характеристики:

• концентрации примесей в высокоомной и низкоомной областях p–n-перехода;
• величины объемных потенциалов (φ _{об n}, φ _{об p}), позволяющие определить положения уровней Ферми в р- и n -областях p–n-перехода, используя формулы (1.5 а), (1.5 б) и, полагая, что концентрации основных носителей заряда в n- и р- областях равны концентрациям донорных и акцепторных примесей (атомы примеси полностью ионизированы), т.е. n_n» N_D и p_p» N_A;
• величину ширины области пространственного заряда соответствующего p–n-перехода, используя формулы (1.31), (1.33).

По полученным и исходным данным строится энергетическая диаграмма в следующей последовательности.

1. Выбирается масштаб – по вертикали в эВ, по горизонтали в мкм или в нм. Напомним, что электрон-вольт – это энергия, которую приобретает электрон, пройдя разность потенциалов 1 В. Связь этой единицы с джоулями следующая: 1 эВ = 1,6·10^-19 Дж. Энергия, выраженная в электрон-вольтах, численно совпадает с соответствующей разностью потенциалов.

2. Проводится (произвольно) горизонтальная линия – линия уровня Ферми в высокоомной области p–n-перехода, обозначается E_fn или E_fр.

3. На расстоянии, равном величине рассчитанного объемного потенциала, выше (в случае, если область р-типа) или ниже (в случае, если область n -типа) уровня Ферми прочерчивается горизонтальная линия, соответствующая уровню середины запрещенной зоны, обозначается E_i.

4. Параллельно линии E_i на расстояниях, равных половине величины запрещенной зоны полупроводника E_g /2, проводятся горизонтальные линии:

- выше E_i – линия уровня дна зоны проводимости, обозначаемая E_c,

- ниже E_i – линия уровня потолка валентной зоны, обозначаемая E_v.

5. Проводятся вертикальные пунктирные линии, обозначающие границы области пространственного заряда р–n-перехода, расстояние между ними равно рассчитанному значению ширины р–n-перехода.

6. Проводится горизонтальная линия, соответствующая уровню Ферми в низкоомной области, таким образом, чтобы она отличалась от линии уровня Ферми в высокоомной области на величину приложенного напряжения смещения U,обозначается E_fр или E_fn.

7. Прочерчиваются линии, соответствующие середине запрещенной зоны, дну зоны проводимости и потолку валентной зоны в низкоомной области р–n-перехода способами, описанными в п. 3 и 4, обозначаются E_i, E_c и E_v.

8. Одинаково обозначенные линии, а также линии уровней Ферми в р- и n- областях соединяются друг с другом соответствующими отрезками прямой линии.

1.3. Структура "металл-полупроводник"

1.3.1.Расчет вольт-амперной характеристики контакта " металл-полупроводник ". Контакт "металл-полупроводник" может быть как омическим, так и выпрямляющим. Омические контакты металла с полупроводником являются обязательными элементами любого активного или пассивного полупроводникового прибора или устройства, так как они осуществляют электрическую связь между элементами прибора и внешней цепью, обусловленную линейной вольт-амперной характеристикой.

Выпрямляющие контакты "металл-полупроводник" используются для построения активных элементов на основе барьеров Шоттки и характеризуются нелинейной зависимостью тока, протекающего через контакт, от приложенного к нему напряжения.

Для идеального контакта "металл–полупроводник" высота барьера равна разности между работой выхода металла и электронным сродством полупроводника n-типа проводимости:

 

qφ_b = q (φ_m – æ),

 

где æ – сродство к электрону.

Высота барьера Шоттки qφ_b при идеальном контакте между металлом и полупроводником p-типа определяется аналогично

 

qφ_b = E_g – q (φ_m – æ).

 

Для данного полупроводника и любого металла сумма высот барьеров, образующихся при контакте металла с полупроводником n- и p-типа, должна быть равной ширине запрещенной зоны

 

q (φ_bn + φ_bp) = E_g.

 

Максимальное значение напряженности электрического поля E в полупроводнике рассчитывается по формуле

 

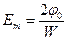. (1.39)

Здесь W – толщина обедненного слоя полупроводника.

В условиях равновесия W определяется выражением

, (1.40)

 

где N – концентрация электрически активных примесей в полупроводнике.

При значительной толщине обедненного слоя W в приконтактной области полупроводника, а именно если

 

, (1.41)

 

где l – длина свободного пробега носителей заряда, справедлива диффузионная теория выпрямления.

Она приводит к следующему уравнению вольт-амперной характеристики выпрямляющего контакта полупроводника с металлом:

 

, (1.42)

 

где σ ₀ – удельная электропроводность полупроводника,

φ_b – высота барьера Шоттки.

Когда для контакта "металл–полупроводник" выполняется условие, обратное (1.36):

 

(1.43)

 

носители заряда, пролетая через обедненный слой, почти не рассеиваются решеткой полупроводника.

Теория выпрямления такого слоя называется диодной теорией. В этом случае уравнение вольт-амперной характеристики контакта полупроводника с металлом имеет вид

 

, (1.44)

где – постоянная Ричардсона.

Длина свободного пробега носителей заряда может быть определена из выражения

 

,

 

где μ – подвижность электронов или дырок в соответствующем полупроводнике; m ^* – эффективная масса носителей заряда.

 

1.3.2. Расчет вероятности туннелирования электрона сквозь барьер Шоттки. Для структуры "металл-полупроводник" распределение потенциальной энергии электрона в области барьера Шоттки можно считать треугольным и аппроксимировать функцией

 

E(x)=φ_b−qE∙x,(1.45)

 

где φ_b – энергия (высота) барьера Шоттки. Тогда подстановка (1.40) в выражение для расчета вероятности квантовомеханического туннельного перехода электрона с энергией Е ₀ сквозь потенциальный барьер произвольной формы

 

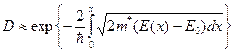(1.46)

 

позволяет получить выражение для расчета вероятности туннелирования электрона сквозь барьер Шоттки в виде

 

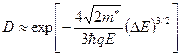. (1.47)

 

В выражениях (1.46) и (1.47) m^* – эффективная масса электронов в полупроводнике; DE = φ_b – Е ₀ (Е ₀ – энергия электрона, туннелирующего из полупроводника в металл); – постоянная Планка; E – напряженность электрического поля в полупроводнике, рассчитывается по формуле (1.39).

 

1.3.3.Барьерная емкость контакта "металл-полупроводник" определяется по формуле

 

[Ф], (1.48)

 

где S – площадь контакта "металл-полупроводник".

 

1.3.4. Порядок построения энергетических диаграмм контакта "металл-полупроводник". Для построения энергетической диаграммы контакта "металл-полупроводник" при заданном напряжении смещения U необходимо определить следующие электрофизические характеристики:

• концентрацию примесей в полупроводнике;
• величину объемного потенциала (φ _{об n}, φ _{об p}), позволяющую определить положение уровня Ферми в полупроводнике, используя формулы (1.5 а), (1.5 б), полагая, что концентрация основных носителей заряда равна концентрации донорной или (в зависимости от типа проводимости полупроводника) акцепторной примеси, т.е. и (атомы примеси полностью ионизированы);
• величину высоты барьера Шоттки, используя справочные данные из прил. 6;
• величину ширины области пространственного заряда в полупроводнике по формуле (1.40).

По полученным и исходным данным строится энергетическая диаграмма в следующем порядке.

1. Выбирается масштаб: по вертикали в эВ, по горизонтали в мкм или в нм (см. п. 1.2.8. Порядок построения энергетической диаграммы p–n-перехода).

2. Проводится (произвольно) отрезок прямой линии, соответствующий положению уровня Ферми в металле, обозначается E_fM.

3. Проводятся вертикальные пунктирные линии, обозначающие границы области пространственного заряда в полупроводнике, расстояние между ними равно рассчитанному значению W.

4. Проводится отрезок прямой линии, соответствующий уровню Ферми в полупроводнике, таким образом, чтобы он совпадал с линией уровня Ферми в металле (т.к. контакт "металл-полупроводник" в равновесии), обозначается E_fр или E_fn.

5. На расстоянии, равном величине рассчитанного объемного потенциала, выше (в случае, если полупроводник р-типа) или ниже (в случае, если полупроводник n -типа) от уровня Ферми проводится отрезок прямой линии, соответствующий середине запрещенной зоны полупроводника, обозначается E_i.

6. Параллельно линии E_i на расстояниях, равных половине величины запрещенной зоны полупроводника E_g /2 проводятся отрезки прямых линий:

- выше E_i – линия уровня дна зоны проводимости, обозначаемая E_c,

- ниже E_i – линия уровня потолка валентной зоны, обозначаемая E _v.

7. На границе раздела "металл-полупроводник" от уровня Ферми в металле проводится вертикальный отрезок, его длина равна величине барьера Шоттки qj_b.

8. В области пространственного заряда полупроводника энергетические линии, соответствующие E_c, E_v и E_i, представляются изогнутыми относительно нейтральной области полупроводника по параболическому закону. Величина (по вертикали) изгиба энергетических уровней на поверхности полупроводника в точке x = 0 (граница раздела металл-полупроводник) равна контактной разности потенциала "металл-полупроводник" qj ₀.

 

1.4. Структура "металл-диэлектрик-полупроводник"

 

1.4.1. Расчет дифференциальной емкости МДП-структуры. Структура МДП является основой ряда дискретных приборов твердотельной электроники, а также элементов интегральных схем. К их числу относятся полевые транзисторы (МДП-транзисторы), приборы с зарядовой связью (ПЗС-структуры), варикапы и др. В основе их функционирования лежит принцип эффекта поля.

Эффектом поля называют явление изменения продольной проводимости полупроводника под действием поперечного электрического поля. Суть этого явления заключается в воздействии на поверхность полупроводника внешним полем и управлении величиной поверхностного изгиба зон. Данный эффект используется также в некоторых методах диагностики поверхностных состояний в полупроводниках.

МДП-транзисторы являются униполярными активными элементами интегральных схем. Наряду с этим, МДП-структуры можно использовать в качестве конденсаторов и резисторов, номинальные значения которых изменяются в определенных пределах при изменении приложенного потенциала к управляющему электроду. Кроме того, МДП-структуры могут также выполнять функции элемента памяти. Особенно широко МДП-транзисторы применяются при построении цифровых интегральных схем.

Существует две разновидности МДП-транзисторов: с индуцированным и проводящим каналами.

Анализ показывает, что вольт-амперная стоковая характеристика МДП-транзистора с индуцированным каналом описывается формулой

 

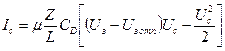, (1.49)

 

где Z и L – соответственно ширина и длина канала; μ – подвижность носителей заряда в канале; C_D – удельная емкость МДП-структуры, определяемая соотношением , в котором ε_D – диэлектрическая проницаемость подзатворного диэлектрика, d – его толщина; U_c – напряжение между истоком и стоком; U_з – напряжение на затворе; U_{з отп} – напряжение отпирания, при котором формируется (индуцируется) проводящий канал между истоком и стоком.

Из выражения (1.49) видно, что напряжение отпирания, называемое также пороговым напряжением U_пор МДП-транзистора, является его важным параметром.

При этом напряжении в приповерхностной области полупроводника формируется пространственный заряд, соответствующий режиму сильной инверсии.

Упрощенное выражение для порогового напряжения для «n» – канального МДП-транзистора имеет вид

 

. (1.50)

 

Соответствующее выражение для «p» – канального МДП-транзистора

 

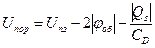. (1.51)

 

В (1.50) и (1.51) U_пз – напряжение плоских зон; φ_об – объемный потенциал; Q_s – полная поверхностная плотность заряда в полупроводнике.

Для МДП-структуры в предположении, что разность работ выхода электрона из металла и полупроводника не равна нулю, а в диэлектрике МДП-структуры и на границе раздела диэлектрик-полупроводник отсутствует заряд поверхностных состояний, напряжение плоских зон будет определяться разностью потенциалов φ_MS соответствующей разности работ выхода U_пз = φ_MS.

Величину φ_MS можно определить из соотношения

 

 

для полупроводника n-типа и

 

 

для полупроводника p-типа.

Второе слагаемое в выражениях (1.50) и (1.51) определяет величину поверхностного потенциала φ_S, при котором начинается сильная инверсия

 

.

 

Третье слагаемое в (1.50) и (1.51) определяет величину падения напряжения на слое диэлектрика, которое, используя закон Гаусса, можно определить как

 

,

 

где E_D – напряженность электрического поля на диэлектрике.

Таким образом, для идеальной МДП-структуры величина порогового напряжения определяется выражением

 

, (1.52)

 

где N = N_А или N_D, в зависимости от типа проводимости полупроводниковой подложки МДП-транзистора. Знаки (+) и (–) определяются типом проводимости индуцированного канала между истоком и стоком. Величина объемного потенциала определяется соотношением .

Максимальная толщина обедненного слоя в приповерхностной области полупроводника формируется в режиме сильной инверсии и находится из выражения

 

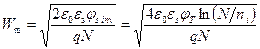. (1.53)

 

При изготовлении интегральных микросхем, а также силовых полупроводниковых приборов в качестве затворного электрода широко применяются слои сильнолегированного поликремния. Для поликремниевых затворов n⁺-типа, где уровень Ферми практически совпадает с положением дна зоны проводимости, эффективная работа выхода φ_m равна величине сродства к электрону в кремнии (æ_Si = 4,15 В). В поликремниевых затворах p⁺-типа, где уровень Ферми совпадает с потолком валентной зоны, эффективная работа выхода .

В прил. 7 приведена зависимость разности работ выхода φ_ms от уровня легирования кремниевой подложки для МДП-структур с затворными электродами из Al, Au и поликремния n⁺ и p⁺-типа.

Из этих графиков следует, что в зависимости от материала затвора при нулевом напряжении смещения приповерхностная область полупроводника МДП-структуры может оказаться практически в любом состоянии (от обогащения до инверсии).

Полная удельная емкость МДП-структуры определяется соотношением

 

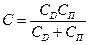
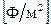, (1.54)

 

которое соответствует последовательному соединению емкости ОПЗ полупроводника и емкости диэлектрика

 

. (1.55)

 

Величина емкости C_D определяется толщиной диэлектрика и представляет собой максимально возможную емкость всей структуры C_D = C _max.

Емкость ОПЗ полупроводника не является постоянной и ее величина определяется изменением поверхностной плотности заряда Q_S при изменении приложенного к МДП-структуре напряжения:

 

.

 

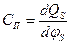В отсутствие разности работ выхода приложенное напряжение делится между полупроводником и диэлектриком:

 

.

 

Таким образом, можно определить зависимость полной емкости МДП-структуры от приложенного напряжения.

Особый интерес представляет величина полной емкости МДП-структуры в режиме сильной инверсии C _min, т.е. при U = U _пор, так как она определяет значение коэффициента перекрытия по емкости поверхностного варикапа.

 

.

 

Соответствующее U _пор значение удельной дифференциальной емкости идеальной МДП-структуры равно

.

 

1.4.2. Порядок построения энергетической диаграм-мы МДП-структуры. Для построения энергетической диаграммы МДП-структуры в режиме сильной инверсии необходимо определить следующие электрофизические характеристики:

• концентрацию примесей в полупроводнике;

• величину объемного потенциала (φ _{об n}, φ _{об p}), позволяющего определить положение уровня Ферми в полупроводнике, используя формулы (1.5 а), (1.5 б) и, считая, что концентрация основных носителей заряда равна концентрации донорной или (в зависимости от типа проводимости полупроводника) акцепторной примеси (атомы примеси полностью ионизированы), т.е. и ;
• величину изгиба энергетических зон в приповерхностной области полупроводника, в которой локализован пространственный заряд, соответствующего режиму сильной инверсии ;
• величину ширины области пространственного заряда в приповерхностной области полупроводника W_m в режиме сильной инверсии;
• значение толщины диэлектрического слоя;
• величину порогового напряжения.

По полученным и исходным данным строится энергетическая диаграмма.

1. Выбирается масштаб: по вертикали в эВ, по горизонтали в мкм или в нм (см. п. 1.2.8. Порядок построения энергетической диаграммы p–n-перехода).

2. Проводятся вертикальные пунктирные линии, обозначающие границы "затвор-диэлектрик" и "диэлектрик-полупроводник". Проводится (произвольно) горизонтальная линия – линия уровня Ферми в полупроводнике, обозначается E_fn (или E_fp).

3. Проводится вертикальная пунктирная линия, обозначающая границу области пространственного заряда в приповерхностной области полупроводника, расстояние от нее до границы с диэлектриком равно рассчитанному значению W_m.

4. На расстоянии, равном величине рассчитанного объемного потенциала, выше (в случае, если полупроводник р-типа) или ниже (в случае, если полупроводник n-типа) от уровня Ферми проводится горизонтальная линия, соответствующая уровню середины запрещенной зоны полупроводника, обозначается E_i.

5. Параллельно линии E_i на расстояниях, равных половине величины запрещенной зоны полупроводника E_g /2, проводятся горизонтальные линии:

- выше E_i – линия уровня дна зоны проводимости, обозначаемая E_c,

- ниже E_i – линия уровня потолка валентной зоны, обозначаемая E_v.

6. В пределах 0 ¸ W_m линии, соответствующие E_c, E_v и E_i, представляются изогнутыми относительно нейтральной области полупроводника по параболическому закону. Величина (по вертикали) изгиба энергетических уровней на поверхности полупроводника в точке x = 0 (граница раздела "диэлектрик-полупроводник") равна удвоенному значению объемного потенциала, т.е. qj_s = 2qj _об.

7. В ОПЗ через точку пересечения линий уровня Ферми и середины запрещенной зоны полупроводника проводится вертикальная пунктирная линия, обозначающая границу слоя инверсной проводимости.

8. Отрезками горизонтальных линий отображается область диэлектрика, указывается толщина диэлектрика d.

9. Проводится горизонтальная линия, соответствующая уровню Ферми в затворе, таким образом, чтобы она располагалась выше (или ниже) линии уровня Ферми в полупроводнике (подложке) на величину порогового напряжения (qU _пор), обозначается E_fМ.