Отношение  называется предпорядком или квазипорядком, если Р рефлексивно и транзитивно.
называется предпорядком или квазипорядком, если Р рефлексивно и транзитивно.
Отношение  называется частичным порядком, если Р рефлексивно, транзитивно и антисимметрично. Т.е. частичный порядок – это антисимметричный предпорядок.
называется частичным порядком, если Р рефлексивно, транзитивно и антисимметрично. Т.е. частичный порядок – это антисимметричный предпорядок.
Множество, с заданным на нём частичным порядком называется частично упорядоченным множеством (ЧУМ)
Пусть <A,≤> - ЧУМ. Тогда элемент  называется наибольшим, если
называется наибольшим, если  . Элемент
. Элемент  называется наименьшим, если
называется наименьшим, если  . Элемент
. Элемент  называется максимальным, если для него нет большего, т.е.
называется максимальным, если для него нет большего, т.е. 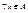 , если
, если  , то
, то  . Элемент
. Элемент  называется минимальным, если для него нет меньшего, т.е.
называется минимальным, если для него нет меньшего, т.е. 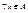 , если
, если  , то
, то 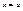 .
.
Наименьший элемент всегда минимален (наибольший – максимален). Обратное неверно.
Наибольший элемент часто называют единицей. Наименьший – нулем.
Диаграммы Хассе:
Рассмотрим ЧУМ <A,≤>. Говорят, что элемент y покрывает элемент x, если x≤y и x≠y не существует такого элемента z, что x<z<y. Если множество А конечно, то частично упорядоченное множество <A,≤> можно представить в виде схемы, в которой каждый элемент изображается точкой на плоскости, и если y покрывает х, то точки х и y соединяются отрезком, причем точку х располагают ниже y. Такие схемы называются диаграммами Хассе.
Частичный порядок ≤ на множестве А называется линейным порядком, если любые два элемента x и y из множества А сравнимы, т.е. x≤y или y≤x.
Линейный порядок ≤ на множестве А называется полным, если каждое непустое подмножество множества А имеет наименьший элемент. Пара <A,≤>, в которой отношение ≤ является полным порядком на множестве А, называется вполне упорядоченным множеством.
10. Алгебраические системы: определение и примеры. Понятие полугруппы, моноида, группы; задание с помощью таблицы Кэли.
Алгебраической системой A=<A,∑> называется пара, где А – непустое множество, носитель алгебраической системы; ∑ - сигнатура алгебраической системы, множество функциональных и предикатных символов с указанием их местности. Примеры: <ω, +(2), •(2), ≤(2), 0(0), 1(0)>; <R, +(2), -(2), e(0)>
Сигнатура ∑ называется функциональной (предикатной), если она не содержит предикатных (функциональных) символов. Система А называется алгеброй (моделью), если ее сигнатура функциональна (предикатна).
Группоид – алгебраическая система с одной двухместной операцией. Эта единственная операция часто обозначается символом •. Если А – конечное множество, то действия операции • можно задать квадратной таблицей, в которой для каждой пары  записан результат действия. Такая таблица называется таблицей Кэли группоида А. (Что-то наподобие таблицы умножения).
записан результат действия. Такая таблица называется таблицей Кэли группоида А. (Что-то наподобие таблицы умножения).
Полугруппа – группоид, у которого операция • ассоциативна. Т.е. x•(y•z)=(x•y) •z/
Моноид – полугруппа, для которой существует элемент e называемый единицей, такой, что e•x=x•e=x.
Группа – моноид, в котором для любого элемента  существует элемент
существует элемент 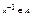 , называемый обратным к x, такой, что x•x-1=x-1•x=e.
, называемый обратным к x, такой, что x•x-1=x-1•x=e.
Группа называется коммутативной или абелевой, если x•y=y•x.




