Множество значений параметров, при которых система является устойчивой.
!Task 41
Система, имеющая 2 чисто мнимых корня, а остальные имеют отрицательные вещественные части … Правильный ответ:находится на границе устойчивости колебательного типа.
!Task 42
Необходимым и достаточным условием устойчивости систем первого и второго порядка является положительность коэффициентов её характеристического уравнения … Правильный ответ:Да.
!Task 43
Корни характеристического полинома системы равны. Система будет устойчива при выполнении условия …
Правильный ответ: 
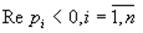
!Task 44
Один из корней системы имеет нулевое значение, а остальные имеют отрицательные вещественные части, тогда... Правильный ответ:система находится на границе устойчивости нейтрального типа.
!Task 45
Среди корней системы есть пара чисто мнимых, а остальные корни имеют отрицательную вещественную часть тогда... Правильный ответ:система находится на границе устойчивости колебательного типа.
!Task 46
Вещественные части корней характеристического полинома устойчивой непрерывной системы … Правильный ответ:меньше нуля.
!Task 47
Укажите правильные утверждения … Правильный ответ:Для того, чтобы система была устойчивой необходимо и достаточно, чтобы вещественные части корней характеристического уравнения были меньше нуля.
!Task 48
Укажите правильные утверждения … Правильный ответ:При наличии хотя бы одного корня с положительной вещественной частью система неустойчива.
!Task 49
Укажите правильные утверждения … Правильный ответ:Для того, чтобы система была устойчивой необходимо и достаточно, чтобы все корни характеристического уравнения системы находились в левой полуплоскости.
!Task 50
Для оценки устойчивости линейной непрерывной системы должны быть исследованы … Правильный ответ:Свободная составляющая решения дифференциального уравнения системы.
!Task 51
Система, описываемая системой дифференциальных уравнений в форме Коши с матрицей состояния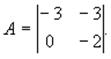
будет … Правильный ответ: Неустойчива.
!Task 52
Система, описываемая системой дифференциальных уравнений в форме Коши с матрицей состояния
будет … Правильный ответ: Неустойчива.
!Task 53
Система, описываемая системой дифференциальных уравнений в форме Коши с матрицей состояния
будет … Правильный ответ: Неустойчива.
!Task 54
Система, описываемая системой дифференциальных уравнений в форме Коши с матрицей состояния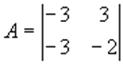
будет … Правильный ответ: Неустойчива.
3. Дидактическая единица ГОС: Устойчивость непрерывных систем управления
4. Тема задания: Корневые методы исследования устойчивости линейных систем
!Task 1Устойчивость линейной динамической системы может быть определена по характеру …
Правильный ответ:
свободного движения.
Если yo(t) - общее решение линейного однородного уравнения, описывающего поведение системы, и
то такая система …
Правильный ответ:
асимптотически устойчива.
!Task 3
Переходная составляющая решения дифференциального уравнения, описывающего поведение линейной системы, имеет вид
уп(t) = C1exp(α1t) + C2exp(α2t) +...+ Ckexp(αkt),
где: Сi, αi - вещественные числа, i = 1...k; t - время. Необходимым и достаточным условием устойчивости такой системы является условие …
Правильный ответ:
αi<0, i = 0,...,k.
!Task 4
Переходная составляющая решения дифференциального уравнения, описывающего поведение линейной системы, имеет вид
уп(t) = C1exp(αt) + C2exp(β1t) +...+ C3exp(β2t),
где: С1, С2, С3, α - вещественные числа; β1, β2 - комплексно сопряженные числа; t - время. Необходимым и достаточным условием устойчивости такой системы является условие
Правильный ответ:
α<0 и Re β1 <0.
Расположение корней характеристического уравнения замкнутой системы показано на рисунке.
Автоматическая система …
Правильный ответ:
неустойчива.
!Task 6
Расположение корней характеристического уравнения замкнутой системы показано на рисунке.
Автоматическая система …
Правильный ответ:
устойчива.
Расположение корней характеристического уравнения замкнутой системы показано на рисунке.
Автоматическая система …
Правильный ответ:
на колебательной границе устойчивости.
Расположение корней характеристического уравнения замкнутой системы показано на рисунке.
Автоматическая система …
Правильный ответ:
на границе устойчивости нейтрального типа.
Движение системы описывается дифференциальным уравнением
где: y(t) - выходная переменная, g(t) - задающее воздействие, t - время.
Автоматическая система …
Правильный ответ:
устойчива.
!Task 10
Движение системы описывается дифференциальным уравнением
где: y(t) - выходная переменная, g(t) - задающее воздействие, t - время.
Автоматическая система …
Правильный ответ:
на колебательной границе устойчивости.
!Task 11
Движение системы описывается дифференциальным уравнением
где: y(t) - выходная переменная, g(t) - задающее воздействие, t - время.
Автоматическая система будет находиться на границе устойчивости при …
Правильный ответ:
А > 0.
Движение системы описывается дифференциальным уравнением
где: y(t) - выходная переменная, g(t) - задающее воздействие, t - время.
Автоматическая система …
Правильный ответ:
на границе устойчивости нейтрального типа.
Передаточная функция замкнутой системы имеет вид
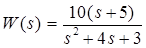
Замкнутая система …
Правильный ответ:
устойчива.
Передаточная функция разомкнутой системы имеет вид
При замыкании отрицательной обратной связью система будет …
Правильный ответ:
на колебательной границе устойчивости.
!Task 15
Передаточная функция разомкнутой системы имеет вид
Замкнутая отрицательной обратной связью система будет устойчивой при значениях коэффициента передачи …
Правильный ответ:
К > 1.
!Task 16
Передаточная функция разомкнутой системы имеет вид
Замкнутая неединичной отрицательной обратной связью с коэффициентом передачи Ко =2 система будет устойчивой при значениях коэффициента передачи …
Правильный ответ:
К > 2.
!Task 17
Передаточная функция разомкнутой системы имеет вид
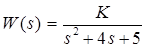
Замкнутая единичной отрицательной обратной связью система будет на границе устойчивости апериодического типа при значении коэффициента передачи …
Правильный ответ:
К = -5.
Передаточная функция замкнутой системы имеет вид
Переходной процесс системы будет сходящимся и носить колебательный характер при значениях коэффициента передачи
Правильный ответ:
К > 4.
Передаточная функция замкнутой системы имеет вид
Переходной процесс системы будет сходящимся и носить апериодический характер при значениях коэффициента передачи …
Правильный ответ:
0 < К < 25.
!Task 20
Передаточная функция разомкнутой системы имеет вид
При замыкании единичной положительной обратной связью система будет …
Правильный ответ:
неустойчива.
Передаточная функция разомкнутой системы имеет вид
При замыкании единичной положительной обратной связью система будет …
Правильный ответ:
неустойчива.
Передаточная функция разомкнутой системы имеет вид
Замкнутая единичной отрицательной обратной связью система будет на границе устойчивости колебательного типа при значении коэффициента передачи …
Правильный ответ:
К = -4.
!Task 23
Для управления неустойчивым объектом используется пропорциональный регулятор, как показано на рисунке
Переходной процесс замкнутой системы будет сходящимся и носить апериодический характер при настройке регулятора …
Правильный ответ:
К > 0,1.
Для управления объектом, описываем интегрирующим звеном, используется пропорциональный регулятор, как показано на рисунке
Переходной процесс замкнутой системы будет сходящимся и носить апериодический характер при настройке регулятора
Правильный ответ:
Кр > 0.
Для управления объектом, описываемым апериодическим звеном первого прядка, используется интегральный регулятор, как показано на рисунке
Переходной процесс замкнутой системы будет сходящимся и носить апериодический характер при настройке регулятора …
Правильный ответ:
0 < Кр < 0,4.
3. Дидактическая единица ГОС: Структурные представления систем управления
4. Тема задания: Структурные преобразования систем
!Task 1
Если H1(s)=5 - передаточная функция прямой связи, а H2(s)=3/s - передаточная функция отрицательной обратной связи, то результирующая передаточная функция будет определяться выражением …
Правильный ответ:
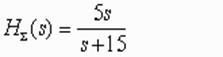
!Task 2
Если H1(s)=2 - передаточная функция прямой связи, а H2(s)=1/s - передаточная функция отрицательной обратной связи, то результирующая передаточная функция будет определяться выражением …
Правильный ответ:
!Task 3
Если H1(s)=2 - передаточная функция прямой связи, а H2(s)=1/s+1 - передаточная функция отрицательной обратной связи, то результирующая передаточная функция будет определяться выражением …
Правильный ответ:
!Task 4
При параллельном соединении двух звеньев с передаточными функциями H(s)=2/s и H(s)=3/(s+1) результирующая передаточная функция будет иметь вид …
Правильный ответ:
!Task 5
При параллельном соединении двух звеньев с передаточными функциями H(s)=2s и H(s)=4/(s+2) результирующая передаточная функция будет иметь вид …
Правильный ответ:
!Task 6
При параллельном соединении двух звеньев с передаточными функциями H(s)=2s и H(s)=5 результирующая передаточная функция будет иметь вид …
Правильный ответ:
!Task 7
При параллельном соединении двух звеньев с передаточными функциями H(s)=2/(s+3) и H(s)=3/(s+5) результирующая передаточная функция будет иметь вид …
Правильный ответ:
!Task 8
При параллельном соединении двух звеньев с передаточными функциями H(s)=2/s и H(s)=5 результирующая передаточная функция будет иметь вид …
Правильный ответ:
!Task 9
При параллельном соединении двух звеньев с передаточными функциями H(s)=2 и H(s)=5/(s+1) результирующая передаточная функция будет иметь вид …
Правильный ответ:
!Task 10
При последовательном соединении двух звеньев с передаточными функциями H(s)=2/s и H(s)=3/(s+1) результирующая передаточная функция будет иметь вид …
Правильный ответ:
!Task 11
При последовательном соединении двух звеньев с передаточными функциями H(s)=2s и H(s)=4/(s+2) результирующая передаточная функция будет иметь вид …
Правильный ответ:
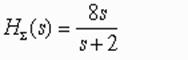
!Task 12
При последовательном соединении двух звеньев с передаточными функциями H(s)=2s и H(s)=5 результирующая передаточная функция будет иметь вид …
Правильный ответ:
!Task 13
При последовательном соединении двух звеньев с передаточными функциями H(s)=2/(s+3) и H(s)=3/(s+5) результирующая передаточная функция будет иметь вид …
Правильный ответ:
!Task 14
При последовательном соединении двух звеньев с передаточными функциями H(s)=2/s и H(s)=5 результирующая передаточная функция будет иметь вид …
Правильный ответ:
!Task 15
При последовательном соединении двух звеньев с передаточными функциями H(s)=10/(s+3) и H(s)=5/(s+5) результирующая передаточная функция будет иметь вид …
Правильный ответ:
!Task 16
При переносе узла с входа на выход звена исходная схема
преобразуется следующим образом …
Правильный ответ:
!Task 17
При переносе узла с выхода на вход звена исходная схема
преобразуется следующим образом …
Правильный ответ:
!Task 18
При переносе сумматора с входа на выход звена исходная схема
преобразуется следующим образом …
Правильный ответ:
!Task 19
При переносе сумматора с выхода на вход звена исходная схема
преобразуется следующим образом …
Правильный ответ:
3. Дидактическая единица ГОС: Структурные представления систем управления
4. Тема задания: Типовые динамические звенья и их математическое описание
!Task 1
Установите соответствие между видом дифференциального уравнения и названием типового динамического звена
1.
2. 
3. 
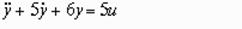
4. 
Правильное соответствие:
апериодическое звено первого порядка
апериодическое звено второго порядка
консервативное звено
дифференцирующее звено
!Task 2
Установите соответствие между видом дифференциального уравнения и названием типового динамического звена
1.
2. 
3. 
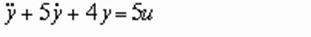
4. 
Правильное соответствие:
апериодическое звено первого порядка.
апериодическое звено второго порядка.
консервативное звено.
интегрирующее звено.
!False
дифференцирующее звено
!Task 3
Установите соответствие между видом дифференциального уравнения и названием типового динамического звена
1.
2.
3.
4.
Правильное соответствие:
апериодическое звено первого порядка.
реальное дифференцирующее звено.
дифференцирующее звено.
интегрирующее звено
!Task 4
Установите соответствие между видом дифференциального уравнения и названием типового динамического звена
1.
2.
3.
4.
Правильное соответствие:
апериодическое звено первого порядка.
изодром.
дифференцирующее звено.
интегрирующее звено.
!Task 5
Установите соответствие между видом дифференциального уравнения и названием типового динамического звена
1.
2.
3.
4.
Правильное соответствие:
апериодическое звено первого порядка.
изодром.
реальное дифференцирующее звено.
консервативное звено.
!Task 6
Установите соответствие между видом дифференциального уравнения и названием типового динамического звена
1.
2.
3.
4.
Правильное соответствие:
апериодическое звено первого порядка.
колебательное звено второго порядка.
апериодическое звено второго порядка.
консервативное звено.
!Task 7
Установите соответствие между видом дифференциального уравнения и названием типового динамического звена
1.
2.
3.
4.
Правильное соответствие:
реальное дифференцирующее звено.
колебательное звено второго порядка.
консервативное звено.
дифференцирующее звено
!Task 8
Установите соответствие между видом дифференциального уравнения и названием типового динамического звена
1.
2.
3.
4.
Правильное соответствие:
изодром.
реальное дифференцирующее звено.
дифференцирующее звено
интегрирующее звено.
!Task 9
Установите соответствие между видом дифференциального уравнения и названием типового динамического звена
1.
2.
3.
4.
Правильное соответствие:
апериодическое звено первого порядка.
колебательное звено второго порядка
консервативное звено.
интегрирующее звено.
!Task 10
Установите соответствие между видом дифференциального уравнения и названием типового динамического звена
1.
2.
3.
4.
воздействиях на звено.
Правильное соответствие:
консервативное звено.
апериодическое звено второго порядка.
колебательное звено второго порядка.
реальное дифференцирующее звено.
!Task 11
Установите соответствие между видом передаточной функции и названием типового динамического звена
1.
2.
3.
4.
Правильное соответствие:
апериодическое звено первого порядка.
апериодическое звено второго порядка.
консервативное звено.
дифференцирующее звено.
!Task 12
Установите соответствие между видом передаточной функции и названием типового динамического звена
1.
2.
3.
4.
Правильное соответствие:
апериодическое звено первого порядка.
апериодическое звено второго порядка.
консервативное звено.
интегрирующее звено.
!Task 13
Установите соответствие между видом передаточной функции и названием типового динамического звена
1.
2.
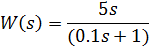
3.
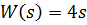
4.
Правильное соответствие:
апериодическое звено первого порядка.
реальное дифференцирующее звено.
