С использованием преобразования Лапласа

Второй часть лабораторной работы будет решение дифференциальных уравнений с использованием преобразования Лапласа. Пример решения представлен ниже.

Решить дифференциальных уравнений с использованием преобразований Лапласа:

.

Допустим, входной сигнал имеет форму единичного ступенчатого воздействия, т.е. . Тогда изображение входного сигнала .

Производим преобразование исходного ДУ по Лапласу и подставляем :

Определяется выражение для :

.

Оригинал полученной функции отсутствует в таблице оригиналов и изображений (таблица 1). Для решения задачи его поиска дробь разбивается на сумму простых дробей с учетом того, что знаменатель может быть представлен в виде

s(s + 2)(s + 3)

Сравнивая получившуюся дробь с исходной, можно составить систему из трех уравнений с тремя неизвестными:

Решая систему уравнений, получим следующие корни:

Следовательно, дробь можно представить как сумму трех дробей: .

Теперь, используя табличные функции, определяется оригинал выходной функции:

.

Функция y(t) является решением дифференциального уравнения.

Таблица 1 преобразований Лапласа

Оригинал x(t)	Изображение X(s)

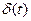
Записываем заданные дифференциальные уравнения.

 

 

Решение:

По заданным дифференциальным уравнениям записать передаточные

Функции и оценить устойчивость звеньев по корням

Характеристических уравнений (используется корневой критерий)

Пример решения представлен ниже.

Из полученного выражения во второй части лабораторной работы получаем передаточную функцию:

Теперь использую корневой критерий, оцениваем устойчивость системы.

Корневой критерий формулируется следующим образом: линейная АСР устойчива, если все корни характеристического уравнения лежат в левой полуплоскости. Инными словами, все действительные части комплексных корней должны быть отрицательными. В противном случае система неустойчива.

Так как в данном случае все корни отрицательны(-2; -3), делаем вывод, что система устойчива.

Решение:

Вывод:

 

Практическая работа № 2

Исследование частотных характеристик

Типовых динамических звеньев

Цель работы: определение динамических свойств элементарных звеньев и показателей качества переходного процессапо полученным частотным характеристикам.

Общие сведения

Частотной характеристикой называется реакция звена (системы) на синусоидальное входное воздействие.

Отношение выходного сигнала к входному при подаче на вход синусоидальной функции называется частотной передаточной функцией или амплитудно-фазовой характеристикой (АФЧХ).

W (jω) = A (ω) e^{jφ ( ω )} = P (ω) +jQ (ω),

где P (ω)–вещественная часть амплитудно-фазовой характеристики; Q (ω)–мнимая часть амплитудно-фазовой характеристики.

Так же, как и передаточная функция ω (s), частотная передаточная функция представляет собой отношение выходной координаты к входной.

Только в первом случае это отношение рассматривается в изображениях по Лапласу, а во втором случае - в виде отношения гармонических сигналов в показательной форме:

где А (ω) –модуль частотной передаточной функции или амплитудная характеристика,

где φ (ω) –аргумент частотной передаточной функции или фазовая характеристика.

Амплитудной характеристикой называется зависимость амплитуды выходного сигнала от частоты.

Фазовой характеристикой называется зависимость сдвига фаз выходного сигнала от частоты по отношению к входному.

Удобной формой представления частотных характеристик являются логарифмические частотные характеристики, состоящие из логарифмической амплитудной характеристики (ЛАХ) и логарифмической фазовой характеристики (ЛФХ).

Логарифмическая амплитудная характеристика апериодического звена представляется в виде

Единицей измерения амплитуды на выходе звена (системы) является децибел. Один бел соответствует увеличению мощности сигнала в 10 раз, два бела – в 100 раз. Децибел равен одной десятой части бела.

Частота ω в логарифмических частотных характеристиках измеряется в декадах. Одна декада соответствует изменению частоты в 10 раз.

Фазовый сдвиг φ (ω) при построении в логарифмическом масштабе остается в тех же единицах (в радианах или в градусах).

Логарифмической амплитудной характеристикой (ЛАХ) называется зависимость относительной амплитуды, выраженной в децибелах, от частоты, выраженной в декадах.

Логарифмической фазовой характеристикой (ЛФХ) называется зависимость фазового сдвига, выраженного в радианах или в градусах, от частоты, выраженной в декадах:

φ (ω) = f (lg(ω)).