Требования к временным характеристикам

 

Типичная переходная функция системы второго порядка изображена на рисунке 1.

 

 

Рис. 1 Типичная переходная функция САР при единичном ступенчатом воздействии

 

Время нарастания T_r определим как время, необходимое для изменения переходной функции от 10% до 90% от ее установившегося значения.

Максимальное значение переходной функции обозначим М_t, время достижения максимума T_p, а процентное превышение установившегося значения будем рассчитывать по формуле

процентное превышение = (4)

На рис. 1 установившееся значение выходной величины принято x_ss = 1.

Время установления T_s – это время, необходимое для того, чтобы выходной сигнал вошел в определенную зону, прилегающую к установившемуся значению, и далее оставался в пределах этой зоны. Ширину зоны обычно принимают равной ±5% или ±2% от установившегося значения

, (5)

где Т – постоянная времени звена (системы); ξ – коэффициент затухания; ω_п – собственная частота колебаний.

Время достижения максимума T_p или максимальное перерегулирование определяется следующим выражением

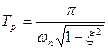; (6)

Время нарастания при ширине зоны 5%:

.

 

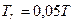Исходные данные (из табл. 2):

- k – коэффициент передачи =

- Т – постоянная времени =

- ξ –коэффициент затухания =

- τ – время запаздывания =

 

Проводим моделирование переходного процесса каждого элементарного звена при подаче на его вход единичного ступенчатого воздействия (табл. 3).

Таблица 2 – Математические модели типовых динамических звеньев

Вид звена	Уравнение динамики	Передаточная функция ω (s)
Безынерционное звено	Xвых (t) = k·xвх (t)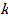
Апериодическое звено
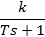
Колебательное звено
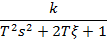
Дифференцирующее звено
Реальное дифференцирующее звено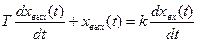
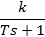
Интегрирующее звено
Запаздывающее звено	xвых (t) = xвх (t-τ)
Неустойчивое звено первого порядка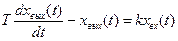
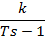
Неустойчивое звено второго порядка

 

 

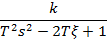
Таблица 3 – Расчет математической модели типовых динамических звеньев

 

Вид звена	Уравнение динамики	Передаточная функция ω (s)	Ts	Tp	Tr	Структурная схема	Нуль к	Полюс s
Безынерционное звено	Xвых (t) = k·xвх (t)		4 T		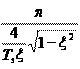0,05 T
Апериодическое звено						-//-
Колебательное звено			-//-	-//-	-//-
Дифференцирующее звено			-//-	-//-	-//-
Реальное дифференцирующее звено			-//-	-//-	-//-	-//-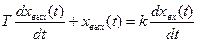
Интегрирующее звено			-//-	-//-	-//-	-//-
Запаздывающее звено	xвых (t) = xвх (t-τ)		-//-	-//-	-//-	-//-
Неустойчивое звено первого порядка			-//-	-//-	-//-	-//-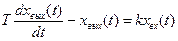
Неустойчивое звено второго порядка			-//-	-//-	-//-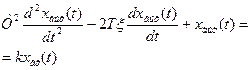

Решение дифференциальных уравнений