Теория физического подобия указывает, что нет необходимости опытным путём изучать связь между отдельными существенными для данного процесса величинами. Проще найти связь между безразмерными комплексами, составленными из этих величин. Каждый физический процесс можно выразить математическим уравнением. Можно, не решая этих уравнений, объединить физические величины в безразмерные комплексы – критерии подобия и получить критериальные уравнения с меньшим числом переменных.
Основными безразмерными критериями тепловых и гидродинамических процессов являются
Критерий Рейнольдса. Представляет собой отношение силы инерции к силе вязкости и определяет характер движения жидкости
,
где w – скорость движения жидкости, м / с;
d – определяющий размер, м;
- коэффициент кинематической вязкости, м 2/ с.
Критерий Прандтля. Характеризует теплофизические свойства теплоносителя.
,
где а – коэффициент температуропроводности, м 2/ с;
ρ – плотность, кг / м 3;
λ – коэффициент теплопроводности, Вт /(м · К); с – теплоёмкость, Дж /(м · К).
Для газов одинаковой атомности число Pr является практически постоянной величиной (для одноатомных Pr 
0,67, двухатомных Pr 0,72 и многоатомных Pr 1).
Критерий Нуссельта. Характеризует интенсивность процесса конвективного теплообмена. Показывает отношение между интенсивностью теплоотдачи и температурным полем в пограничном слое потока.
,
Критерий Грасгофа. Характеризует отношение подъёмной силы, возникающей вследствие теплового расширения жидкости, к силам вязкости.
,
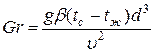где g – ускорение свободного падения, g =9,81 м / с 2;
- коэффициент объёмного расширения, 1/ К;
tc – температура стенки, К;
tж – температура жидкости, К.
Критерий Пекле. Характеризует отношение конвективного потока и потока теплопроводности при теплоотдаче.
.
Критериальные уравнения для различных случаев теплообмена приводятся в специальной литературе. Эти уравнения обычно выводятся на основе экспериментов для каждого отдельного случая практики. Распространять результаты опытов можно только на подобные явления.
Теория подобия устанавливает необходимые и достаточные условия, при которых рассматриваемые явления будут подобными.
Теория подобия позволяет заменить громоздкие, дорогие сооружения небольшими моделями, на которых проводятся эксперименты.
Понятие подобия известно из геометрии, где изучается подобие треугольников. Используя свойство подобных треугольников можно определить высоту дерева, ширину реки и т.п., не производя непосредственных измерений.
