Методические указания
В инженерной практике часто приходится иметь дело с газообразными веществами, близкими по свойствам к идеальным газам и представляющими собой механическую смесь отдельных компонентов различных газов, химически не реагирующих между собой. Это так называемые газовые смеси.
Основным законом, определяющим поведение газовой смеси, является закон Дальтона: полное давление смеси идеальных газов равно сумме парциальных давлений всех входящих в неё компонентов
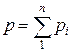 .
.
Состав газовой смеси определяется количеством каждого из газов, входящих в смесь, и может быть задан массовыми или объёмными долями. Массовая доля определяется отношением массы отдельного газа входящего в смесь, к массе всей смеси
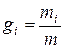 ,
,
где gi – массовая доля компонента смеси;
mi – массы отдельных газов, кг;
m – масса всей смеси, кг.
Объёмной долей газа называется отношение объёма каждого компонента, входящего в смесь, к объёму всей газовой смеси при условии, что объём каждого компонента, отнесён к давлению и температуре смеси

где ri – объёмная доля компонента смеси;
Vi – приведённые объёмы компонентов газов, входящих в смесь, м3;
V – общий объём газовой смеси, м3.
Очевидно, что 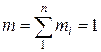 ,
,  .
.
Основные формулы, применяемые при расчётах газовых смесей, приведены в таблице 1.1.1.
Таблица 1.1.1 – Формулы для расчёта газовых смесей
| Состав смеси | Перевод из одного состава в другой | Удельный объём смеси | Кажущаяся молекулярная масса смеси | Газовая постоянная смеси | Парциальное давление |
| Массовые доли | 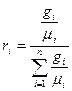
| 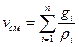
| 
| 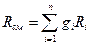
| 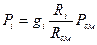
|
| Объёмные доли | 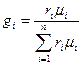
| 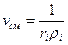
| 
| 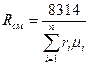
| 
|
Теплоемкостью называют количество теплоты, которое необходимо сообщить телу (газу), чтобы повысить температуру какой-либо количественной единицы на 10 С. В зависимости от выбранной количественной единицы вещества различают удельные мольную 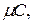 кДж/ (кмоль · К), массовую
кДж/ (кмоль · К), массовую  кДж/ (кг · К) и объемную
кДж/ (кг · К) и объемную 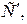 кДж/ (м 3· К) теплоемкости.
кДж/ (м 3· К) теплоемкости.
1 м3 газа в зависимости от параметров его состояния имеет разные массы. В связи с этим объемную теплоемкость всегда относят к массе газа, заключенной в 1 м3 его при нормальных условиях Рн = 101325 Па (760 мм.рт.ст.) и Т = 273 К (t =00 С). Для определения значений перечисленных выше теплоёмкостей достаточно знать величину одной какой-либо из них. Удобнее всего иметь величину мольной теплоемкости. Тогда массовая теплоемкость 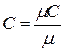 , а объемная теплоемкость
, а объемная теплоемкость  . Объемная и массовая теплоемкости связаны между собой зависимостью
. Объемная и массовая теплоемкости связаны между собой зависимостью  , где
, где  - плотность газа при нормальных условиях.
- плотность газа при нормальных условиях.
Теплоемкость газа зависит от его температуры. По этому признаку различают среднюю и истинную теплоемкость. Если q - количество теплоты, сообщаемой единице количества газа (или отнимаемого от него) при изменении температуры газа от t1 до t2 то средняя теплоемкость впределах температур  . Предел этого отношения, когда разность температур стремится к нулю, называют истинной теплоемкостью.Аналитически последняя определяется, как
. Предел этого отношения, когда разность температур стремится к нулю, называют истинной теплоемкостью.Аналитически последняя определяется, как 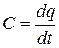 . Теплоемкость идеальных газов зависит не только от их температуры, но и от их атомности и характера процесса. Теплоемкость реальных газов зависит от их природных свойств, характера процесса, температуры и давления. Для газов важное значение имеют следующие два случая нагревания (охлаждения): 1) изменение состояния при постоянном объеме; 2) изменение состояния при постоянном давлении. Обоим этим случаям соответствуют различные значения теплоемкостей. Таким образом, различают истинную и среднюю теплоемкости: а) мольную при постоянном объеме
. Теплоемкость идеальных газов зависит не только от их температуры, но и от их атомности и характера процесса. Теплоемкость реальных газов зависит от их природных свойств, характера процесса, температуры и давления. Для газов важное значение имеют следующие два случая нагревания (охлаждения): 1) изменение состояния при постоянном объеме; 2) изменение состояния при постоянном давлении. Обоим этим случаям соответствуют различные значения теплоемкостей. Таким образом, различают истинную и среднюю теплоемкости: а) мольную при постоянном объеме 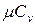 ,
, 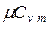 и постоянном давлении
и постоянном давлении 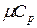 ,
,  ; б) массовую при постоянном объеме
; б) массовую при постоянном объеме 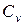 ,
, 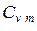 и постоянном давлении
и постоянном давлении  ,
,  ; в) объемную при постоянном объеме
; в) объемную при постоянном объеме 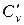 ,
, 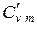 и постоянном давлении
и постоянном давлении 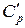 ,
, 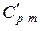 .
.
Между мольными теплоемкостями при р =const и v =const существует следующая зависимость: 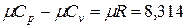 кДж/ (кмоль · К).
кДж/ (кмоль · К).
Для приближённых расчётов при невысоких температурах можно принять значения мольных теплоёмкостей указанные в таблице 1.1.2.
Отношение теплоёмкостей при р =const и v =const обозначается 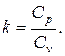
Таблица 1.1.2 – Значения мольных теплоёмкостей при р =const и v =const
| Газы | Мольная теплоёмкость | 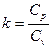
| |

| 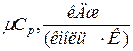
| ||
| Одноатомные | 12,56 | 20,93 | 1,67 |
| Двухатомные | 20,93 | 29,31 | 1,41 |
| Трёх и многоатомные | 29,31 | 37,68 | 1,29 |
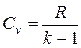 ;
; 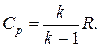
Количество теплоты, которое участвует в процессе нагревания (охлаждения) М, кг или V, м3 газа
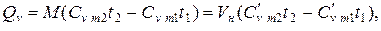
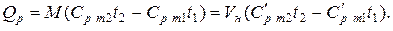
Теплоёмкость газов изменяется с изменением температуры, причём эта зависимость носит криволинейный характер. Нелинейную зависимость истинной теплоёмкости от температуры представляют в виде
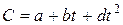 ,
,
где a, b, d – величины постоянные для данного газа.
В расчётах нелинейную зависимость заменяют близкой к ней линейной зависимостью 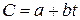 , а средняя теплоёмкость при изменении температуры от t1 до t2
, а средняя теплоёмкость при изменении температуры от t1 до t2
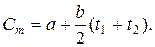
Для средней теплоёмкости в пределах 00- t эта формула принимает вид
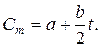
Теплоёмкость смеси идеальных газов
Если смесь газов задана массовыми долями, то её массовая теплоёмкость определяется как сумма произведений массовых долей на массовую теплоёмкость каждого компонента  ,
, 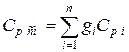 .
.
При задании смеси объёмными долями объёмная теплоёмкость смеси 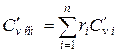 ,
,  .
.
Аналогично мольная теплоёмкость смеси равна сумме произведений объёмных долей на мольные теплоёмкости составляющих смесь газов 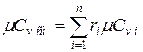 ,
, 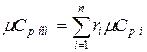 .
.
В приложениях 2-9 приведены теплоёмкости наиболее часто встречающихся в расчётах газов.
Задание №1
Газовая смесь задана в массовых gi или объемных ri долях процентным составом компонентов смеси; давление смеси Р см, МПа, объём смеси V см, м3 температура смеси tсм, 0 С (таблица 1.2.1).
Определить:
1. Состав смеси (если по условию состав смеси задан в объемных долях ri, то следует определить дополнительно состав смеси в массовых долях gi и наоборот);
2. Газовые постоянные компонентов смеси Ri, кДж/ (кг · К);
3. Газовую постоянную смеси Rсм, кДж/ (кг · К) через объёмные и массовые доли;
4. Среднюю молярную массу смеси μсм, кмоль / кг через объемные ri и массовые gi доли;
5. Парциальные давления компонентов Рi, МПа через объемные ri и массовые gi доли;
6. Массу смеси mсм, кг и компонентов смеси mi, кг;
7. Парциальные объёмы  , парциальные удельные объемы vi, м 3/ кг и плотности ρi, кг / м 3 компонентов смеси;
, парциальные удельные объемы vi, м 3/ кг и плотности ρi, кг / м 3 компонентов смеси;
8. Плотности компонентов ρi, кг / м 3 и смеси ρсм, кг / м 3 при заданных условиях Рсм, МПа и tсм,0 С;
9. Плотности компонентов ρi, кг / м 3 при нормальных физических условиях;
10. Плотность смеси ρсм, кг / м 3 при нормальных физических условиях через объемные ri и массовые gi доли;
11. Истинную молярную μС, кДж/ (кмоль · К), объемную 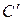 , кДж/ (м 3· К), и массовую С, кДж/ (кг · К) теплоемкости при p =const и v =const для температуры смеси tсм,,0 С;
, кДж/ (м 3· К), и массовую С, кДж/ (кг · К) теплоемкости при p =const и v =const для температуры смеси tсм,,0 С;
12. Среднюю молярную μС, кДж/ (кмоль · К), объемную 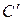 , кДж/ (м 3· К) и массовую С, кДж/ (кг · К) теплоемкости при p =const и v =const для интервала температур Δ tсм,,0 С;
, кДж/ (м 3· К) и массовую С, кДж/ (кг · К) теплоемкости при p =const и v =const для интервала температур Δ tсм,,0 С;
13. Количество теплоты, необходимое на нагревание (охлаждение) в интервале температур Δ tсм,,0 С при р =const и v =const количества вещества 2 кмоль, 5 м3 и 7 кг смеси.
Таблица 1.2.1– Параметры газовой смеси
| № вар | Состав смеси | Давление смеси, Р см, МПа | Объём смеси, V см, м3 | Температура смеси, tсм,, 0 С | Интервал температур, Δ tсм,,0 С | ||||||
| СО2 | Н2 | СО | N2 | Н2О | SO2 | O2 | |||||
| - | - | - | 0,095 | 200-1000 | |||||||
| - | - | - | 0,1 | 300-100 | |||||||
| - | - | - | 0,09 | 100-300 | |||||||
| - | - | - | 0,105 | 600-200 | |||||||
| - | - | - | 0,105 | 1000-100 | |||||||
| - | - | - | 0,085 | 900-200 | |||||||
| - | - | - | 0,07 | 700-500 | |||||||
| - | - | - | - | 0,095 | 500-200 | ||||||
| - | - | - | 0,1 | 800-300 | |||||||
| - | - | - | 0,105 | 600-100 | |||||||
| Продолжение таблицы 1.2.1 | |||||||||||
| № вар | Состав смеси | Давление смеси, Р см, МПа | Объём смеси, V см, м3 | Температура смеси, tсм,, 0 С | Интервал температур, Δ tсм,,0 С | ||||||
| СО2 | Н2 | СО | N2 | Н2О | SO2 | O2 | |||||
| - | - | - | 0,115 | 750-250 | |||||||
| - | - | - | 0,12 | 1000-500 | |||||||
| - | - | - | 0,125 | 300-1300 | |||||||
| - | - | - | 0,105 | 600-900 | |||||||
| - | - | - | 0,085 | 100-400 | |||||||
| - | - | - | 0,12 | 850-350 | |||||||
| - | - | - | 0,10 | 350-750 | |||||||
| - | - | - | 0,09 | 900-600 | |||||||
| - | - | - | 0,1 | 450-300 | |||||||
| - | - | - | 0,105 | 300-150 | |||||||
| - | - | - | 0,105 | 800-300 | |||||||
| - | - | - | 0,1 | 400-300 | |||||||
| - | - | - | 0,095 | 800-300 | |||||||
| - | - | - | 0,115 | 650-150 | |||||||
| - | - | - | 0,085 | 150-1200 | |||||||
| - | - | - | 0,1 | 300-800 | |||||||
| - | - | - | 0,1 | 1200-1000 | |||||||
| - | - | - | 0,09 | 400-900 | |||||||
| - | - | - | 0,095 | 800-600 | |||||||
| - | - | - | 0,1 | 600-100 | |||||||
| - | - | - | 0,11 | 500-1000 | |||||||
| - | - | - | - | 0,10 | 500-200 | ||||||
| - | - | - | 0,085 | 800-250 | |||||||
| - | - | - | 0,10 | 200-700 | |||||||
| - | - | - | 0,095 | 400-100 |
Пример решения задания
Смесь имеет следующий объемный состав:
СО2 =12%; 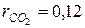 ; ;
| Н 2О =8%; 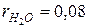 ; ;
|
N2 =75%; 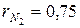 ; ;
| О 2 =5%; 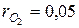 . .
|
Всего 100%; 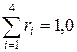 .
.
Объем смеси Vcм =3 м3; давление смеси Рсм =0,1МПа; температура смеси tcм =100 0 С (Тсм =373 К). Температуру, при которой определяется истинная теплоемкость смеси t =20000 С (Т =2273 К) Интервал температур, для которого определяется средняя теплоемкость смеси t1 =2000 С (T1 =473 К); t2 =10000 C (Т2 =1273 К). Провести расчет в соответствии с заданием (п. 1.2)
Решение
1. Определяем состав смеси в массовых долях
 ,
,
где μi – молярная масса компонента смеси, кг / кмоль (приложение 1).
 ;
;
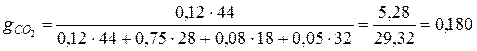 .
.
Аналогично для остальных компонентов смеси

| 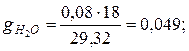
| 
|
Проверка 
2. Определяем газовые постоянные компонентов смеси

| |
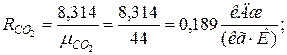
| 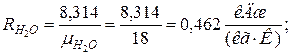
|

| 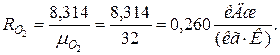
|
3. Определяем газовую постоянную смеси:
а) через объёмные  доли
доли
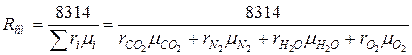 ;
;

б) через массовые 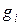 доли
доли

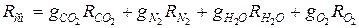 ;
;
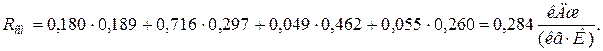
4. Находим среднюю молярную массу смеси
а) через объёмные  доли
доли
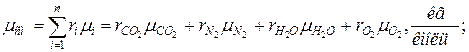
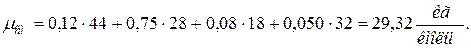
б) через массовые 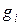 доли
доли
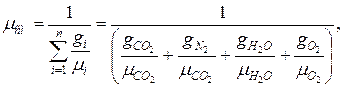
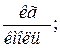

Проверка 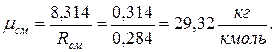
5. Определяем парциальные давления компонентов смеси:
а) через объёмные  доли
доли
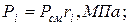
| |

| 
|
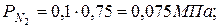
| 
|
б) через массовые 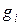 доли
доли
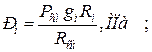
| |
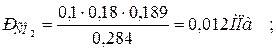
| 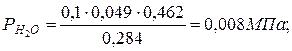
|
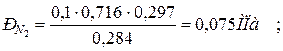
| 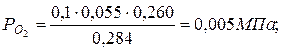
|
Проверка 
6. Находим массу смеси
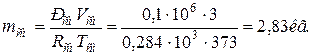
Определяем массу компонентов газовой смеси

| |

| 
|
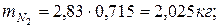
| 
|
Проверка 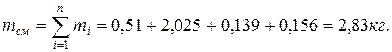
7. Определяем парциальные объемы компонентов смеси
 ; ;
| |
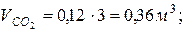
| 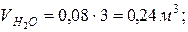
|

| 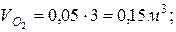
|
Проверка 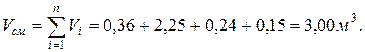
Парциальные удельные объемы компонентов смеси
 ,
где ,
где 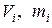 - парциальный объём и масса конкретного газа - парциальный объём и масса конкретного газа
| |
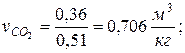
| 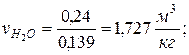
|

| 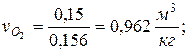
|
Находим плотности компонентов смеси
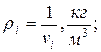
| |

| 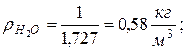
|

| 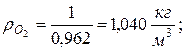
|
8. Плотности компонентов и смеси при заданных условиях Рсм и tсм
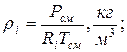
| |
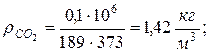
| 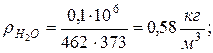
|

| 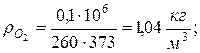
|

| 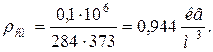
|
9. Определяем плотности компонентов смеси при нормальных физических условиях НФУ (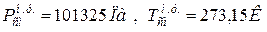 )
)

| |
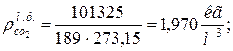
| 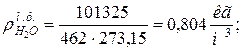
|
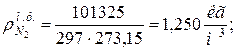
| 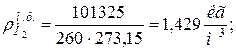
|
10. Определяем плотность смеси при НФУ:
а) через объемные ri доли
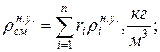
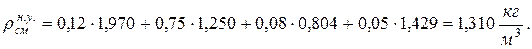
б) через массовые 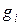 доли
доли
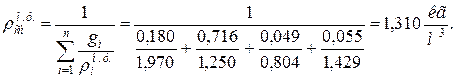
11. Находим истинную теплоемкость смеси (при tсм =20000 С)
а) молярная теплоёмкость смеси при р =const
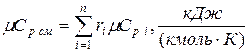 ,
,
где  - молярная изобарная теплоёмкость компонента при температуре смеси tсм, (приложения 2-9).
- молярная изобарная теплоёмкость компонента при температуре смеси tсм, (приложения 2-9).
 ;
;
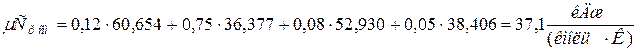 ;
;
молярная теплоёмкость смеси при v =const
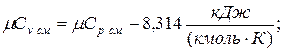
| 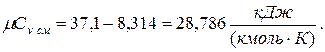
|
б) объемная теплоёмкость смеси при р =const и v =const

| 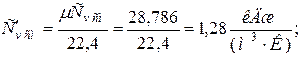
|
в) массовая теплоёмкость смеси при р =const и v =const
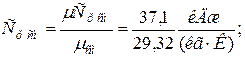
| 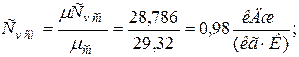
|
12. Определяем среднюю теплоемкость смеси в интервале температур 
а) средняя молярная теплоёмкость смеси при р =const
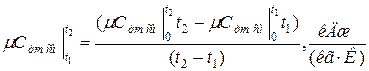
где 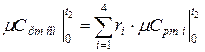 - средняя молярная теплоёмкость смеси при р =const в интервале температур
- средняя молярная теплоёмкость смеси при р =const в интервале температур 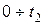 ;
;
 средняя молярная теплоёмкость компонента смеси при р =const в интервале температур
средняя молярная теплоёмкость компонента смеси при р =const в интервале температур 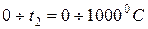 согласно заданию из приложений 2-9.
согласно заданию из приложений 2-9.

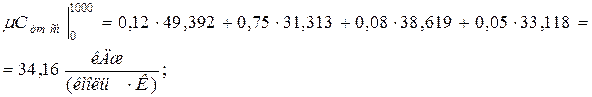
Аналогично находим среднюю молярную теплоёмкость смеси при р =const в интервале температур 
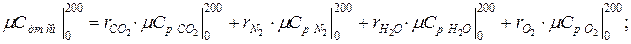
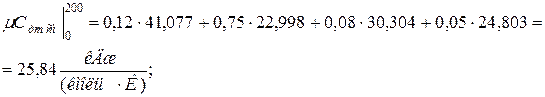
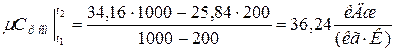 .
.
Средняя молярная теплоёмкость смеси при v =const

б) средняя объемная теплоёмкость при р =const
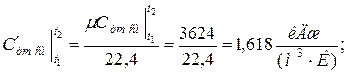 средняя объёмная теплоёмкость при v =const
средняя объёмная теплоёмкость при v =const
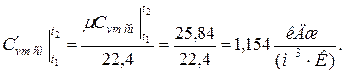 в) средняя массовая теплоёмкость при р =const
в) средняя массовая теплоёмкость при р =const
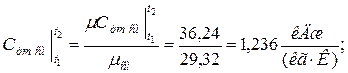 массовая теплоёмкость при v =const
массовая теплоёмкость при v =const
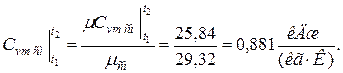 11. Определяем количество теплоты, необходимое на нагревание (охлаждение) смеси при р =const:
а) 2 кмоль смеси
11. Определяем количество теплоты, необходимое на нагревание (охлаждение) смеси при р =const:
а) 2 кмоль смеси
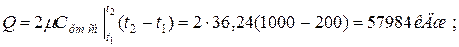 б) 5 м3 смеси
б) 5 м3 смеси
 в) 7 кг смеси
в) 7 кг смеси
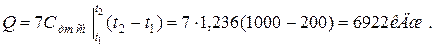 Количество теплоты, необходимое на нагревание смеси при v =const:
а) 2 кмоль смеси
Количество теплоты, необходимое на нагревание смеси при v =const:
а) 2 кмоль смеси
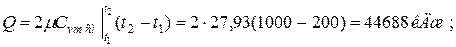 б) 5 м3 смеси
б) 5 м3 смеси
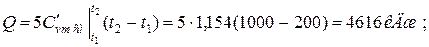 в) 7 кг смеси
в) 7 кг смеси
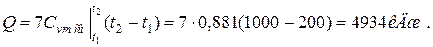
|
Термодинамические циклы
Методические указания
Круговым процессом или циклом называется совокупность термодинамических процессов, в результате осуществления которых рабочее тело возвращается в исходное состояние. Работа кругового процесса изображается в диаграмме P-v площадью, заключённой внутри замкнутого контура цикла, причём работа положительна, если цикл совершается по часовой стрелке (прямой цикл), и отрицательна, если он совершается против часовой стрелки (обратный цикл).Степень совершенства процесса превращения теплоты в работу в круговых процессах характеризуется термическим КПД

Цикл идеальной тепловой машины представляет собой цикл Карно. При его осуществлении предполагается использование горячего источника с постоянной температурой, т. е. фактически с бесконечной теплоемкостью. Цикл состоит из двух адиабат и двух изотерм. Количество подведённой теплоты
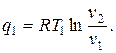
Количество отведённой теплоты
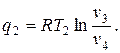
Термический КПД цикла
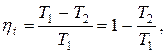
где Т 1 и Т 2 – температуры верхнего и нижнего источников теплоты.
Цикл с подводом теплоты при постоянном объёме состоит из двух адиабат и двух изохор.
Характеристиками цикла являются
- степень сжатия 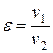 ;
;
- степень повышения давления  .
.
Количество подведенной теплоты
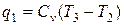 .
.
Количество отведённой теплоты
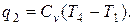
Количество тепла за цикл
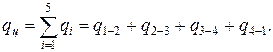
Работа цикла

Изменение внутренней энергии, энтальпии и энтропии за цикл

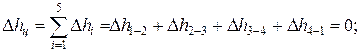
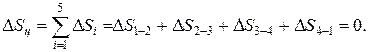
Термический КПД цикла 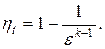
Цикл с подводом теплоты при постоянном давлении состоит из двух адиабат, одной изобары и одной изохоры.
Характеристиками цикла являются
- степень сжатия 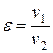 ;
;
- степень предварительного расширения 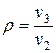 .
.
Количество подведенной теплоты
 .
.
Количество отведённой теплоты
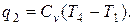
Количество тепла за цикл
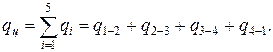
Работа цикла

Изменение внутренней энергии, энтальпии и энтропии за цикл

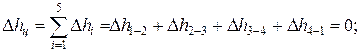
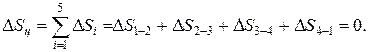
Термический КПД цикла

Цикл с комбинированным подводом теплоты состоит из двух адиабат, двух изохор и одной изобары.
Характеристиками цикла являются
- степень сжатия 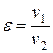 ;
;
- степень повышения давления  ;
;
- степень предварительного расширения 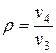 .
.
Количество подведенной теплоты

Количество отведённой теплоты
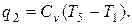
Количество тепла за цикл

Работа цикла

Изменение внутренней энергии, энтальпии и энтропии за цикл
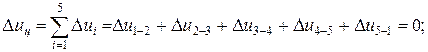
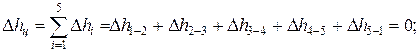
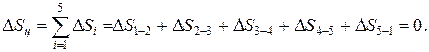
Термический КПД цикла

Во всех случаях с= const.
Цикл газовой турбины с подводом теплоты при постоянном давлении состоит из двух адиабат и двух изобар.
Характеристиками цикла являются
- степень повышения давления в компрессоре 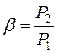 ;
;
- степень сжатия 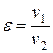 ;
;
- степень расширения 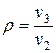 .
.
Термический КПД цикла
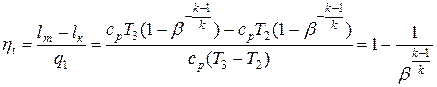 или
или 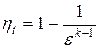 .
.
Цикл газовой турбины с подводом теплоты при постоянном объёме состоит из двух адиабат, одной изохоры и одной изобары
Характеристиками цикла являются
- степень сжатия 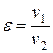 ;
;
- степень добавочного повышения давления  ;
;
- степень расширения 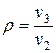 .
.
Термический КПД цикла
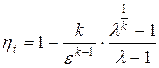 .
.
Так как уходящие из газовой турбины продукты сгорания имеют достаточно высокую температуру, то для повышения экономичности газотурбинного агрегата вводят регенерацию, т.е. предварительный подогрев сжатого в компрессоре воздуха за счёт теплоты, уходящих газов. Термический КПД цикла турбины с подводом теплоты при р= constс полной предельной регенерацией и адиабатным сжатием

Термический КПД цикла турбины с подводом теплоты при v= constc предельной регенерацией и адиабатным сжатием
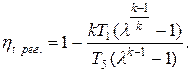
Коэффициент полезного действия идеального цикла ГТУ
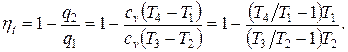
При этом теплоемкость ср принята для простоты постоянной. Одной из основных характеристик цикла является степень повышения давления в компрессоре  . Тогда коэффициент полезного действия идеального цикла ГТУ
. Тогда коэффициент полезного действия идеального цикла ГТУ
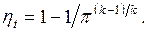
Задание №2
Для заданного варианта цикла теплового двигателя (2.2.1 – 2.2.5) выполнить следующие теоретические, расчетные и графические работы:
1. Дать краткое, описание цикла в целом и характеристику каждого его процесса;
2. Определить параметры р, v, T во всех характерных точках цикла;
3. Провести полный термодинамический расчет каждого процесса;
4. Вычислить термодинамические характеристики цикла;
5. Вычислить термический КПД идеализированного цикла, у которого теплообменом в процессах сжатия и расширения пренебрегают;
6. Вычислить термический КПД цикла Карно осуществляемого в том же интервале температур и энтропии;
7. Изобразить цикл в р - v и Т - S координатах;
8. Определить коэффициент заполнения цикла;
9. Определить среднеинтегральную температуру процесса отвода тепла;
10. На основе расчета сделать заключение и результаты свести в таблицу.
Во всех случаях в качестве рабочего тела принимать воздух. Расчет произвести на 1 кг рабочего тела. Учитывать зависимость теплоемкости от температуры.






