Тема 7. Многогранные поверхности

Вопросы самоконтроля

1. Какие поверхности называют многогранными?

2. Что называют гранью, ребром? Какие им присваивают названия?

3. Чем отличается призма от пирамиды?

4. Чем задаются многогранники на комплексном чертеже?

5. Как определяется видимость ребер и граней?

6. Какие многогранники называют правильными?

7. Чем определяется принадлежность точки или какой-либо линии поверхности многогранника?

8. Что представляет собой фигура сечения многогранника плоскостью?

9. Запишите алгоритм решения задачи о построении точек пересечения прямой линии с поверхностью многогранника. Можно ли установить общность между указанной задачей и задачей о построении точек пересечения прямой линии с плоскостью общего положения?

10. Какие основные способы построения линий пересечения гранных поверхностей существуют?

11. В чем заключается сущность “способа ребер” и “способа граней”?

12. В каком порядке следует соединять линии пересечения многогранников?

13.Как выбирается простейшие секущие плоскости при построении линии пересечения.

Упражнения

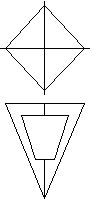
9.1.1. Построить проекции и определить видимость ребер и граней пирамиды. S - вершина, АВСD - основание. Достроить фронтальную проекцию точки Е, принадлежащей грани SАВ.

9.1.2 Построить проекции и определить видимость ребер и граней призмы АВС.

9.1.3 Построить проекции сечения пирамиды SАВС плоскостью S(S1).

 

9.1.4 Построить точки пересечения прямой l с поверхностью призмы АВС A'В'С'.

9.1.5Построить три проекции детали с отверстием.

 

 

Задачи

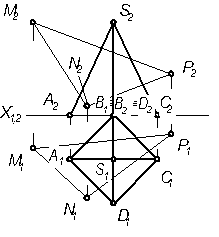
9.2.1 Построить проекции сечения пирамиды SАВС плоскостью S(КLМ). Для решения можно воспользоваться способом преобразования чертежа.

 

9.2.2 Построить проекции сечения призмы АВС А'В'С' плоскостью S(МNР).

9.2.3 Построить проекции сечения пирамиды SАВС плоскостью S(МNР).

 

 

9.2.4Найти точки пересечения прямой m с поверхностью тетраэдра. SABC определить видимость прямой линии относительно поверхности.

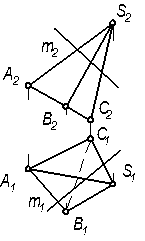
9.2.5 Построить точки пересечения прямой t с поверхностью пирамиды SABC.

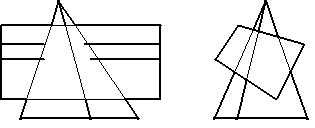
9.2.6 Дана пятиугольная пирамида SABCD со сквозным отверстием, имеющим на фронтальной плоскости проекций форму пятиугольника. Постройте горизонтальную проекцию этого отверстия.

9.2.7 Построить проекции линии пересечения многогранников. определить видимость ребер и граней.

Примеры решения задач:

Задача 1 Задана фронтальная проекция точек М(М₂) и N (N₂) на видимых гранях поверхности.

Решение: Так как каждая грань – это плоскость, ограниченная многоугольником, для грани действуют все признаки инцидентности, определенные для плоскости.

 

Для построения горизонтальной проекции точки М₁ нужно в грани построить любую прямую, проходящую через точку М, тогда соответствующие проекции точки будут лежать на проекциях этой прямой. Удобно использовать прямую, параллельную ребру основания, например (1₂М₂ || (В₂С₂)→(1₁М₁) ||(В₁С₁). Можно также через проекцию N₂ 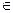(SBC) и вершину S₂ провести прямую (S₂2 ₂)→(S₁2₁) и по линии связи взять N₁. В призме через N₂ проводим прямую линию (N₂2₂)|| (B₂B¹₂) и на ней по линии связи (N₂N₁) находим.N₁. использование свойства параллельности и заданных вершин сокращает объем работы.

Задача 2 Построить линию сечения пирамиды плоскостью Г.

Решение. На рисунке показана линия (1–2–3) сечения пирамиды плоскостью Г (Г₂) , которая строится по точкам 1₂ –2₂ – 3₂ пересечения фронтальных проекций ребер с проекцией секущей плоскости.

 

 

 

Фигура сечения (1 – 2 – 3) многогранника плоскостью Г, которая параллельна его основанию, подобна фигуре основания..

Задача 3 Построить линию пересечения прямой l(ll) с многогранной поверхностью.

Решение. Для определения точек (MN) пересечения прямой l с многогранной поверхностью используют проецирующую плоскость. Например, , далее строят сечение (1–2–3) поверхности и в пересечении проекции прямой с многоугольником сечения находят искомые точки:

. Видимость определяется с помощью конкурирующих точек.

Можно вести плоскость ∆ параллельно боковым ребрам призмы. Для этого на прямой l выбирают точку 1(l₁ – l₂), через нее проводят прямую b (b₁b₂)параллельно проекциям боковых ребер и определяют линию пересечения (2 – 3) (2₂ – 3₂) (2₁ – 3₁) плоскости основания призмы с построенной плоскостью. Плоскость Δ(l∩b)пересечет призму по прямым параллельным боковым ребрам. Начинаются эти прямые в точках 4 ₁и 5₁ пересечения следа (2₁–3₁) с фигурой основания. Их пересечение с l ₁ определит точки M₁ –→ M₂ и N₁→ N₂ пересечения прямой с призмой.

 

 

 

Задача 4 Построить линии пересечения пирамиды и призмы способом ребер.При выборе плоскостей посредников рекомендуется проанализировать возможные варианты и выбрать наиболее простой. Для решения задачи выбраны фронтальные плоскости уровня Θ||Γ||Σ||П₂. Они удобны тем, что пересекают пирамиду по треугольникам, подобным треугольнику G₂ S₂ L₂.

Построения сводятся к тому, что на пересечении проекции Θ₁ плоскости Θ, проходящей через ребро EE^' призмы, с ребрами пирамиды отмечаем проекции 6₁,7₁,8₁ точек, по линиям связи отмечаем 6₂, 8₂ и через них проводим прямые, параллельные соответственно ребрам G₂ S₂. и L₂ S₂.

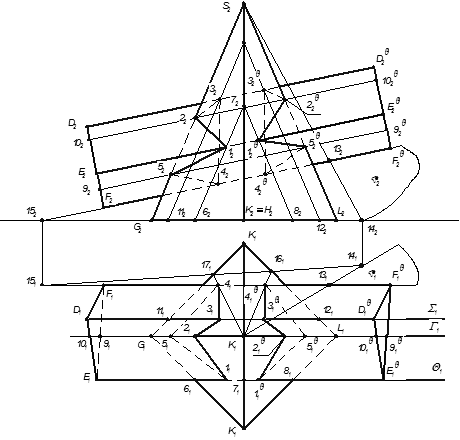
Эти прямые пересекутся в точке 7₂ ребра K₂ S₂ и в точках 1 1^'₂ 1₂' и с проекцией ребра призмы. По линиям связи находим Точки 1(1₁1₂)=(EE^') (GSK) и 1^'() = ….. являются точками пересечения ребра призмы с гранями пирамиды. Отрезок …. Проходит внутри пирамиды. Точки лежат на видимых гранях призмы и пирамиды, следовательно, они тоже видимые. Плоскость… проходит через ребра …. И …. Пирамиды и пересекают призму по прямоугольнику (). Точки 2……….. являются видимыми точками пересечения боковых ребер пирамиды с гранями призмы. Отрезки ……являются частью линии пересечения многогранников. Горизонтальные проекции () и () не видны, так как принадлежат невидимой на виде сверху грани () призмы. Через ребро ….. проведена плоскость.

Через точки 11 и 12 проводим прямые параллельно боковым ребрам пирамиды ….. и отмечаем точки ……; их пересечения с ребром … призмы. соединяем …… основными линиями, так как точки видимые, а ….. - штриховыми линиями, так как точки 3 и 3₁ принадлежат невидимым на фронтали проекциям грани GSH. и LSH. пирамиды.

Для определения точек 4 и 4^' пересечения ребра FF^׀. Призмы с пирамидой были также использованы плоскости уровня.

Соединяем точки 3–4 и 4–5 с учетом их видимости. Фигуры (1–2–3–4–5) и (1^'–2^'–3^'–4^'–5^') являются линиями пересечения данных многогранников. Если нужно выполнить отверстие в многограннике, то эта линия будет являться контуром этого отверстия.

Дополнительные задачи

Задача 1 Построить линию пересечения пирамиды с плоскостью общего положения

Задача 2 Построить линию пересечения пирамиды с плоскостью общего положения.

Задача 3 Построить профильную проекцию детали с вырезом