Прямых и плоскостей
Вопросы самоконтроля.
1. Сформулируйте условие параллельности двух прямых в пространстве и на комплексном чертеже.
2. Сформулируйте условие параллельности прямой и плоскости в пространстве и на комплексном чертеже. Как построить прямую, параллельную данной плоскости?
3. Сформулируйте условие параллельности двух плоскостей в пространстве и на комплексном чертеже.
4. В чем сущность теоремы о проецировании прямого угла?
5. Сформулируйте условие перпендикулярности прямой и плоскости в пространстве и на комплексном чертеже. Кратко запишите это условие.
6. Сформулируйте условие перпендикулярности двух плоскостей в пространстве и на комплексном чертеже. Кратко запишите это условие.
Упражнения
6.1.1 Провести прямую, параллельную прямой m и пересекающую прямую l в точке А.
| 6.1.2 Построить горизонтальную проекцию m, скрещивающейся с линией n. Построить конкурирующие точки, определить их видимость.
|
6.1.3 Через точку К провести прямую, параллельную плоскости S(А, l).
| 6.1.4 Провести плоскость, параллельную заданной плоскости АВС, через точки D. E. F. L.
|
6.1.7 На каком из чертежей изображена прямая n, перпендикулярная плоскости ∑?
| |
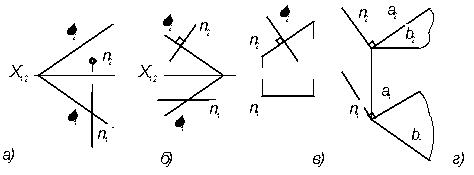
6.1.5 Из точки А опустите перпендикуляр на плоскость β (АВС) и определить его основание и длину.
| 6.1.6Построить в точке А перпендикуляр к плоскости ∑ (m  n) и отложите на нем отрезок
|
Задачи
6.2.3 Из точки А восстановить перпендикуляр к плоскости АВС и отложите на нем отрезок длиной l. Составить алгоритм решения задачи.
| 6.2.4 Определить расстояние от точки Е до плоскости ABCD.
|
6.2.1 Через точку А провести плоскость, параллельную заданной плоскости S.
а) б)
6.2.2 Через две скрещивающиеся прямые провести две параллельные плоскости.
1)
| 2)
|
6.2.5 Через точку М провести плоскость, перпендикулярную к двум данным плоскостям P(aIIb) и Q(ABC).
Примеры решения задач:
Задача 1 Определить расстояние от точки D до плоскости Σ(АВС).
Решение: Из геометрии известен признак перпендикулярности: прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости. Определить расстояние от точки D(D1 D2) до плоскости Σ(АВС). Построим в плоскости горизонталь 
и фронталь 
и через точку D проведем прямую 
, то есть D 
и. 
.
В общем случае нормаль n не ограничена. Но если определяется расстояние от точки D до плоскости, то на линии выделяется отрезок DE.
У которого точка 
называется основанием перпендикуляра. Она определена с помощью посредника 
: 
Задача 2 Определить расстояние от точки А до прямой 1 общего положения
Решение: Для определения расстояния от точки А(А1 А2) до прямой l(l1 l2) общего положения на чертеже поступают так:
– Через точку А проводят плоскость 
, которую задают горизонталью 
и фронталью 
; имеем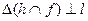 
;
– Определяют точку 
– Отрезок [AB]([A 1B1] [A2 B2]) равен расстоянию от точки А до прямой l в проекциях
Задача 3 Через заданную прямую линию m провести плоскость ∆, перпендикулярную плоскости Σ (DEF).
Решение: Две плоскости взаимно перпендикулярны, если в любой из них можно построить прямую, перпендикулярную другой плоскости.
Если через прямую nÖa провести плоскость b, то плоскости a и b будут взаимно перпендикулярны.
Но через прямую линию n можно провести множество плоскостей, которые называют пучком плоскостей. Чтобы из этого пучка выделить конкретную плоскость b или g, достаточно в этой плоскости задать прямую, параллельную или пересекающуюся с n или точку В не принадлежащую прямой n.
Построим горизонталь h(h2 (F2 – 12 )→h1 ) и фронталь f(f1 (D1 – 21 )→f2 ) плоскости Выберем точку А на прямой l(А2 Î l2→А1) и через нее проведем прямую nÖ(h∩f)(n2 Öf2. n1 Öh1). Так мы построим b(l∩n)Öa(DEF).
Если требуется выяснить перпендикулярность двух плоскостей, то нужно попытаться построить в одной из них прямую, перпендикулярную другой плоскости.
Дополнительные задачи
6.4.1 Построить недостающую проекцию отрезка СD, каждая точка которого равноудалена от точек А и В. Построить  , если 
| 6.4.2 Построить проекции равнобедренного треугольника KMN с основанием MN вершиной K, лежащей на прямой l.
|
6.4.3 Из данной точки А превести прямую, перпендикулярную плоскости, заданной следами и найти его основание
| 6.4.4 Построить горизонтальную проекцию ∆ АВС, плоскость которого параллельна плоскости ∑ (f h) /
|
6.4.5 Построить точку F, симметричную точке D относительно плоскости ∑ (f h
| 6.4.6 Через точку С плоскости Г(С,а) проведите плоскость 
|
