ВВЕДЕНИЕ
Начертательная геометрия изучает способы построения плоских изображений пространственных геометрических объектов, их геометрические свойства и методы решения пространственных геометрических задач на этих изображениях, что необходимо будущим специалистам при использовании чертежей в их производственной деятельности.
Методические указания предназначены для студентов при самостоятельной подготовке к лабораторным занятиям по начертательной геометрии.
Рассмотренные в пособии задачи сгруппированы по темам и используются студентами при самостоятельной подготовке к очередному занятию. Для этого они должны:
- решить задачи предыдущей темы;
- изучить теоретический материал по заданной теме и ответить на вопросы самоконтроля;
- выполнить упражнения по заданной теме;
- часть задач по теме решаются на лабораторных занятиях при помощи преподавателя, а часть задаются для домашнего решения.
В начале занятия преподаватель проверяет решенные студентами самостоятельно задачи предыдущей темы, теоретическую подготовку студентов и решение упражнений по заданной теме. В конце каждой темы рассматривается пример решения типовой задачи с поэтапным выполнением чертежей. Приступая к решению упражнений новой темы, полезно ознакомиться с соответствующим примером и следовать ему в оформлении чертежа. В конце каждой темы приводятся дополнительные задачи. Правильное решение дополнительных задач студентами дает им возможность принять участие в олимпиаде по начертательной геометрии, которая проводится в конце семестра для выявления сильных студентов по курсу. В приложении пособия приводятся тесты по темам для самоконтроля знаний, изученного материала.
В процессе работы с пособием студенты учатся практическим приемам, применяемым при решении задач, что позволяет им выработать навыки и умения самостоятельного их решения. По мере накопления этого опыта студент начинает мыслить самостоятельно на профессиональном уровне.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ И
ОФОРМЛЕНИЮ ЗАДАЧ
При решении задач необходимо руководствоваться следующими рекомендациями:
1. По данным проекциям геометрических фигур, составляющим исходные данные задачи, представить их форму и взаимное расположение в пространстве как по отношению друг к другу, так и относительно плоскостей проекций.
2. Наметить «пространственный» план решения задачи и установить последовательность выполнения геометрических операций, при помощи которых может быть получен ответ на поставленную задачу. На этой стадии решения задачи следует обращаться к теоремам из курса элементарной геометрии разделы «Планиметрия» и «Стереометрия», а также к теоретическому материалу в учебниках и лекциях.
3. Определить алгоритм решения задачи, кратко записать последовательность графических построений, используя принятые обозначения и терминологию.
4. Приступить к геометрическим построениям, используя инвариантные свойства параллельного проецирования. При выполнении первых двух пунктов полезно установить также возможное число решений и выявить причины, от которых они зависят.
5. Следует иметь в виду, что, осуществляя геометрические построения, на любом этапе решения задачи имеется возможность контроля правильности их выполнения. Это особенно ценно, если учесть, что в задачниках по начертательной геометрии не содержится ответов. В основе контроля лежат инвариантные свойства параллельного проецирования и теоремы из школьного курса стереометрии.
При графическом решении задачи точность ответа зависит не только от выбора правильного пути её решения, но и от точности выполнения геометрических построений. Поэтому, решая задачу, необходимо пользоваться чертёжными инструментами. Задачи должны решаться в отдельной тетради в клетку для лабораторных занятий. Тип и толщина линий выполняются в соответствии с ГОСТ 2.303-68 ЕСКД. Построения выполняются карандашом. Для облегчения чтения чертежа, получающегося в процессе решения, целесообразно применять цветные карандаши: заданные элементы обводятся черным цветом, вспомогательные построения – синим, искомые элементы – красным. Эту же цель преследует обязательное обозначение всех точек и линий. При этом обозначение следует делать в процессе решения задачи сразу после проведения линии или определения точки пересечения линий. Надписи и буквенные обозначения выполнять стандартным шрифтом в соответствии с ГОСТ 2.304-84 ЕСКД.
Тетрадь с решенными задачами предъявляется преподавателю на экзамене.
ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
А, В, С, D, …или 1, 2, 3, 4, … - обозначение точки; прописные буквы латинского алфавита или арабские цифры.
о – изображение точки (области расположения точки); круг диаметром 2-3 мм тонкой линией от руки.
a, b, c, d, … - линия в пространстве; строчные буквы латинского алфавита.
Γ, Σ, Δ,… -плоскости, поверхности; прописные буквы греческого алфавита.
α, β, γ, δ, … - углы; строчные буквы греческого алфавита.
П – плоскость проекций (картинная плоскость); прописная буква (пи) греческого алфавита.
АВ – прямая, проходящая через точки А и В.
[ AB] – отрезок, ограниченный точками А и В.
[ AB) – луч, ограниченный точкой А и проходящий через точку В.
/ AB /–натуральная величина отрезка[ AB ] (равная оригиналу).
/ Aа /–расстояние от точки А до линии а.
/ AΣ /–расстояние от точки А до плоскости Σ.
/ ab /–расстояние между линиями а и b.
/GD / - расстояние между поверхностями G и D.
≡- совпадение (А≡В – точки А и В совпадают).
║ - параллельны.
^ - перпендикулярны.
∩ - пересечение.
Î - принадлежит, является элементом множества.
^ - угол, например а^b – угол между прямыми а и b.
Ð α - угол α (или число в градусах).
ÐАВС – угол с вершиной в точке В.
Изображение знаков должно выполняться в соответствии с принятыми стандартами оформления технической и научной документации.
ТЕМА 1 КОМПЛЕКСНЫЙ ЧЕРТЕЖ МОНЖА
(точка, прямая )
Вопросы самоконтроля
1. Свойства ортогонального проецирования.
2. Какие элементы входят в аппарат проецирования?
3. Что называется осью проекций?
4. Что называется проекцией точки?
5. Какие прямые называются «линиями связи» и как они расположены относительно оси проекций?
6. Можно восстановить положение точки в пространстве по её проекциям?
7. Чем можно задать прямую линию на комплексном чертеже?
8. Какие прямые называются прямыми общего и частичного положения? Постройте комплексный чертёж.
9. Как располагаются в пространстве две прямые относительно друг друга?
10. Что называется следом прямой?
3.1 Комплексный чертёж точки
Упражнения
| 3.1.1 При каком условии точка А принадлежит плоскости П1? Запишите координаты этой точки. | 3.1.2 Какой координатой определяется расстояние точки А от плоскости П2? |
| 3.1.3 Напишите условие принадлежности точки В оси Y. | 3.1.4 При каком условии точка С будет равноудалена от плоскостей П1, П2, П3? |
3.1.5. Какая из заданных на чертеже точек А, В или С принадлежит плоскости П1?

3.1.6 На наглядном чертеже (рисунок 3.1) построить проекции А2, В1, С1 и D2 точек-A, B, С и D. Определить в каких четвертях лежат эти точки?

Рисунок 3.1
Задачи
| 3.1.7 Построить проекции точек А, В, С и D так, чтобы точка А лежала в плоскости П2, точка В — в плоскости П1, точка С — на оси X, а точка D была бы равноудалена от плоскостей проекций П1, П2, П3. | 3.1.10 Дана точка А (40, 20, 30). Построить проекции точки В, симметричной точке А относительно горизонтальной плоскости проекций П1, и точку С, симметричную точке В относительно фронтальной плоскости проекций П2. Записать координаты точек В и С. Определить в каких четвертях находятся точки А, В и С. |
3.1.8 При каком условии точка А и точка В находятся на одном расстоянии от плоскости П3? Записать координаты точек, определив их на комплексном чертеже.

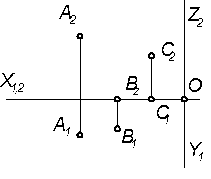
| 3.1.9 Заданы проекции точек А, В и С. Построить:
а) точку Е, которая находится под точкой А на расстоянии 10 мм;
б) точку N над точкой В на расстоянии 15 мм;
в) точку М перед точкой С на расстоянии 20 мм.
г) точку К левее точки А на расстоянии 15 мм и лежащей на оси х.
|
3.2 Комплексный чертёж прямой
Упражнения
3.2.1 При каком условии точка В (осевая проекция Вх которой задана) принадлежит линии 1?
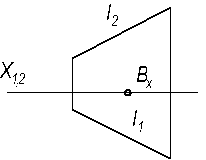
| 3.2.2 Построить проекции отрезка АВ по заданным проекциям точек А и В. Известны разности координат этих точек: YА – YВ = 10; ZВ – ZА = 5.

|
3.2.3 Построить проекции отрезка АВ, который является фронталью, и отрезка АС, который является горизонталью
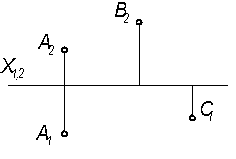
| 3.2.4 На прямой m построить точку, одинаково удаленную от плоскостей П1 и П2.

|
Задачи
3.2.5 Определите положение точек А, В, С, D относительно прямой m.
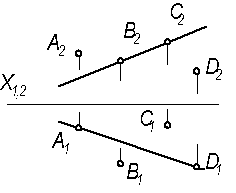
| 3.2.9 На отрезке АВ определить точку С, которая делит отрезок внутренним образом в заданном отношении: СА: СВ = 2: 5.
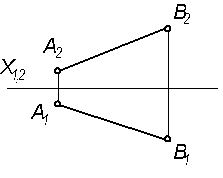
|
3.2.6 Постройте на комплексном чертеже два отрезка соответственно пересекающихся, параллельных, скрещивающихся и конкурирующих прямых.
3.2.7 Через точку А(25, 30, 10) провести отрезок АВ, параллельный плоскости проекций П2 длиной 30 мм под углом 45° к П1. Записать координаты точки В. Сколько решений имеет задача?
3.2.8 Найти натуральную величину отрезка АВ и углы его наклона к плоскостям П1, П2.Координаты точек отрезка А(60, 5, 10), В(10, 20,40).
Примеры решения задач:
Задача 1 Какая из заданных точек А, В, С принадлежит плоскости П1?
Решение. Если точка лежит в плоскости П1, то её высота равна нулю. Поэтому среди заданных точек нужно искать точку с высотой, равной нулю. Высота точки измеряется расстоянием либо от фронтальной проекции точки до оси Х1 2,либо от профильной проекции до оси У3. И если высота точки равна нулю, то эти проекции точки будут лежать на осях Х12 и У3. Этому условию удовлетворяет точка А, у которой проекция А2 лежит на оси Х12, а проекция А3 - на оси У3. Значит точка А расположена в горизонтальной плоскости проекций П1.
Точка С также лежит в плоскости проекций. Об этом говорит расположение её проекций С1 и С3 соответственно на осях Х12 и Z23. Это значит, что у точки С равна нулю глубина. Поэтому она лежит во фронтальной плоскости проекций П2.
Точка В не лежит ни в одной из плоскостей проекций. Она расположена в пространстве.






