Преобразования координат при переходе из одной ИСО в другую.
Если при 
штриховая и нештриховая ИСО совпадают
(
),
и если скорость штриховой ИСО 
постоянна и
направлена вдоль оси Ox, то в какой-то момент вре
мени 
для координат, измеренных в этих ИСО
выполняются следующие равенства:
Рис9. Инерциальные Эти преобразования координат называются
системы отсчёта преобразования Галилея.
Пользуясь ими можно получить формулы
преобразования скорости и ускорения:
=> 
.
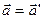Полученный результат говорит о том, что в обеих ИСО II закон Ньютона записывается совершенно одинаково:
– в штриховой ИСО,
- в нештриховой ИСО
Принцип относительности Галилея:
Все законы механики при переходе из одной ИСО в другую не меняют своего вида, то есть инвариантны по отношению к преобразованию координат.
Сформулированный принцип относительности (инвариантности законов механики) позволяет сделать два важных вывода:
Первый: Никакой эксперимент в области механики, проведенный в пределах одной ИСО не позволит определить скорость этой системы.
И второй: Не существует абсолютной системы отсчета. То есть законы механики не позволяют нам обнаружить ИСО, которая является безусловно покоящейся, и определять некоторую абсолютную скорость движения. Скорость всегда относительна.
В дальнейшем эти выводы были обобщены Эйнштейном на электромагнитные и оптические явления, в результате чего появилась специальная теория относительности.
Закон сохранения импульса
Рассмотрим систему взаимодействующих тел. Учтем, что на каждое тело действуют силы со стороны всех остальных тел, а также сила со стороны внешних (находящихся за пределами системы) тел.
по II Закону Ньютона: 
Рис.10 Взаимодействие тел. На рисунке указаны силы,
действующие только на первое тело. Таким же образом
следует учесть силы, действующие на остальные тела
Сложив левые и правые части равенств, получим:
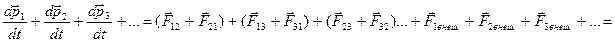
Учитывая, что согласно третьему закону Ньютона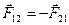 
, 
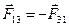и так далее, получим:
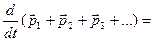
И если 
- суммарный импульс всей системы материальных точек, то для него выполняется условие:
Если окакжется,что 
=0, то система называется замкнутой и тогда для суммарного импульса можно записать: 
или: 
.
Несмотря на взаимодействие между телами замкнутой системы суммарный импульс замкнутой системы изменяться не будет.
Закон сохранения импульса (ЗСИ):
Суммарный импульс в замкнутой системе сохраняется.
Кинетическая энергия
Согласно второму закону Ньютона 
.
Умножив это соотношение на равенство 
, после ряда преобразований получим:
.
Под знаком дифференциала в скобках оказалась величина, которая не будет изменяться при равенстве нулю левой части.
то есть, если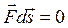 
, то 
Здесь 
– вектор, модуль которого равен 
(бесконечно малой часть пути), а направление совпадает с направлением скорости.
Если 
, то 
Эта величина: 
(или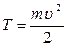 
)
Называется кинетическая энергия..
Если 
≠ 0, то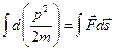 
, и при переходе из состояния (1) в состояние (2)
,
где интеграл 
называется работа.
.
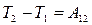Этот результат представляет собой теорему об изменении кинетической энергии:
Изменение кинетической энергии тела равно работе равнодействующей всех сил приложенных к этому телу.
Работа сил
Если 
- равнодействующая сил, приложенных к данному телу, то интеграл, определяющий работу равнодействующей превращается в сумму интегралов:
то есть мы имеем право говорить о работе отдельной силы 
.
Работа силы находится как результат интегрирования скалярного произведения , где 
α- угол между векторами 
и 
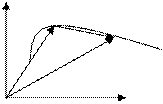
. При вычислении работы можно также использовать вектор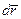 
. Действительно, на бесконекчно малом участке траектории, где 
– дуга, а 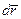- хорда получим, что при Δ 
дуга окажется равной хорде. (см. рис 11)
. 
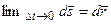. Значит работа может быть со-
считана с помощью интеграла:
.
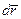
Это говорит о том, что подынтегральное
вы ражение 
можно представить как
.
Работа не совершается и кинетическая
Рис 11. энергия не изменяется при выполнении
К определению работы одного из трех условий:
; 
; 
.
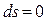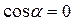В частности, не совершает работу сила гравитационного притяжения при движении спутника (или планеты) по круговой орбите, так как в этом случае .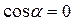
Пример расчета работы: работа силы упругости.
 |
Рис 12. Работа силы упругости
Если мы растягиваем пружину, сила упругости противодействует этому процессу, и работа силы упругости отрицательна. Если растянутая пружина сжимается под действием силы упругости, то работа этой силы будет положительной.
Всегда отрицательной будет работа силы трения, потому что она направлена против движения: α = π и 
.
Мощность
Мощность – это скорость совершения работы.
Средняя мощность: 
, где
A12 – работа, совершаемая за интервал времени Δt12.
Мгновенная мощность: 
, где
- бесконечно малая часть работы, приходящаяся на интервал времени dt
