Рассмотрим выполнение расчетов для исходных данных, заданных в графе «Пример» (см. Варианты индивидуальных заданий). В качестве исходных данных заданы: значения активной мощности нагрузки в процентах от максимальной для соответствующих интервалов времени в течение суток; значение cos j = 0,85; абсолютное значение максимальной активной мощности Pmax = 520 кВт и реактивной мощности Qmax = 320 кВар. Пусть длительность сезона равна 152 сут.
Исходные данные примера заданы для случая cos j = const, т.е. суточные графики активной и реактивной мощности идентичны, и для каждого i -того интервала времени значения реактивной мощности могут быть определены как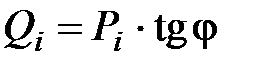 
.
Дискретные функции для расчета суточных ступенчатых графиков активной P (t) и реактивной Q (t) мощности нагрузки реализуются с использованием операторов Add Line и if панели Programming (Программирование), и операторов сравнения панели Boolean (Булева алгебра) так же, как в Работе 3 (см. рис. 108). Отличие реализации состоит в том, что примере к Работе 3 в качестве результата измерения активной мощности в начале каждого интервала D t мы брали соответствующее значение непрерывного контроля P (t), а в данной работе результаты измерения заданы в исходных данных, или предварительно рассчитываются для Q (t) в случае cos j = const.
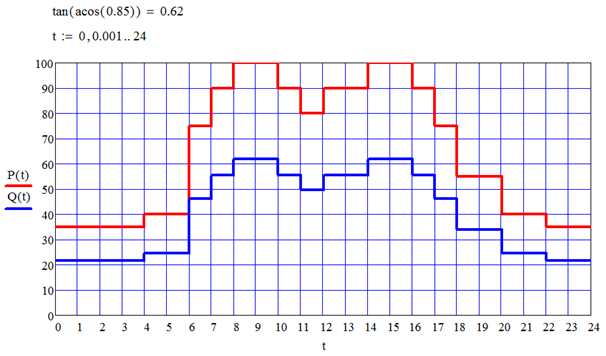
Результат построения суточных ступенчатых графиков активной P (t) и реактивной Q (t) мощности нагрузки для рассматриваемого примера приведен на рис. 116. Там же показан расчет значения 
с использованием встроенных тригонометрических функций MathCAD.
Расчет параметров суточного ступенчатого графика активной нагрузки P (t) приведен на рис. 117. Расчет количества электроэнергии, получаемой потребителем за характерные сутки, реализован по формуле (38) с заданием D t = 1 час, и составляет 8112 кВт·ч. Расчет среднего и среднеквадратичного значений P (t) – по формулам (46) и (41) с учетом того, что рассматриваемый интервал времени t равен 24 часам; коэффициентов заполнения и формы – по формулам (42) и (43). Суточное эквивалентное время использования наибольшей нагрузки через коэффициент заполнения рассчитано по формуле (47) с учетом того, что рассматриваемый интервал времени t равен 24 часам, и через количество электроэнергии – по формуле (45).
| Рис. 116 |
| Рис. 117 |
Для задания дискретной функции расчета упорядоченного суточного ступенчатого графика нагрузки S (t) необходимо, с использованием заданных дискретных функций P (t) и Q (t), рассчитать значения полной мощности S для дискретных моментов времени. Для обеспечения точности построения ступенчатого графика и дальнейших расчетов шаг приращения времени следует выбрать достаточно малым. Далее, рассчитанные значения необходимо отсортировать по убыванию абсолютной величины. Реализовать такой расчет в MathCAD можно с использованием программы, показанной на рис. 118.
| Рис. 118 |
Рассмотрим реализацию программы Prog 1, показанной на рис. 118. Для расчета значений S с некоторым шагом приращения времени t необходимо организовать вычисления в цикле. Оператор цикла for в языке программирования MathCAD требует задания счетчика циклов. Для задания внутри программных модулей переменных, которые «не видны» из других частей рабочего листа, используется оператор локального присваивания. Оператор вставляется нажатием кнопки 
на панели Programming (Программирование). Ни оператор присваивания:=, ни оператор вывода = в пределах программ не применяются.
После присваивания счетчику циклов k нулевого значения следующей строкой программы задается оператор цикла for, у которого соответствующие местозаполнители вводится имя переменной t и диапазон значений (задан ранжированием от 0 до 24 с шагом 0,01). Для создания тела цикла следует поместить линию ввода, как показано на рис. 119– а, и нажать Add Line (рис. 119– б). Для добавления еще одного местозаполнителя (третьей строчки тела цикла) следует еще раз нажать Add Line.
| Рис. 119 |
| а) |
| б) |
В теле цикла с использованием оператора локального присваивания реализованы:
- расчет значения Sk через ранее заданные дискретные функции P (t) и Q (t);
- присвоение переменной tstepk текущего значения времени;
- увеличения счетчика циклов на единицу.
Цикл выполняется до выполнения условия t = 24. В результате вычислений в цикле программой формируется вектор-столбец значений времени tstep и вектор-столбец соответствующих значений полной мощности S, упорядоченные по возрастанию k от 0 до kmax, которое в примере, показанном на рис. 118, равно 1 + 24/0,01 = 2401.
Далее полученный массив необходимо отсортировать по убыванию Sk для дальнейшего построения упорядоченного суточного ступенчатого графика нагрузки S (t). В примере, показанном на рис. 118, это реализовано с использованием встроенных функций MathCAD:
sort (A) – упорядочивает значения вектора-столбца A по возрастанию;
reverse (A) – меняет последовательность значений вектора-столбца A на обратную;
augment (A, В) – формирует новую матрицу из двух ранее заданных А и В, объединяя их бок о бок (А и В должны иметь одинаковое число строк).
Для добавления строк в программу вне тела цикла следует разместить линию ввода как показано на рис. 120– а, и нажать Add Line нужное число раз (рис. 120– б).
| Рис. 120 |
| а) |
| б) |
В результате выполнения программы Prog 1 будет сформирована одноименная матрица, в нулевом столбце которой дискретные значения времени, а в первом столбце – упорядоченные по убыванию дискретные значения полной мощности нагрузки.
Построение упорядоченного суточного ступенчатого графика нагрузки S (t), кВА, по результатам расчета программы Prog 1 показано на рис. 121. Он, по условиям, является характерным для всего сезона, длительность которого составляет 152 сут., что соответствует 3648 часам.
Для расчета и построения сезонного ступенчатого графика нагрузки Sуп (t) воспользуемся встроенной функцией линейной интерполяции
linterp (x, y, t), аргументы которой:
х – вектор-столбец заданных значений аргумента;
у – вектор-столбец заданных значений функции того же размера;
t – значение аргумента линейной интерполяции.
| Рис. 121 |
Так как требуется построить упорядоченный сезонный график, вектор-столбец дискретных значений времени, полученный с использованием программы Prog 1, нужно помножить на длительность сезона (рис. 122).
| Рис. 122 |
Так как исходные данные для построения суточных графиков заданы для одних характерных суток, а, например, не для рабочих и выходных суток, упорядоченный сезонный график по форме повторяет суточный (см. рис. 122).
Расчет нагрузочных потерь электроэнергии по методу характерных суточных режимов по формуле (51) требует вычисления квадратичной сезонной мощности по формуле:
,
где Si – активная мощность на i -той ступени графика нагрузки; D ti – продолжительность ступени; n – число ступеней графика.
Реализация в MathCAD программы Prog 2 для расчета величин Si и времен окончания ступеней графика упорядоченного сезонного графика показана на рис. 123.
| Рис. 123 |
Цикл программы Prog 2 выполняется до выполнения условия t = 3648. В качестве счетчика циклов использована переменная i. В теле цикла проверяются текущее Sуп (t) и следующее Sуп (t +1) значения упорядоченного графика. Если эти значения не равны, то имеет место переход на очередную ступень графика. В этом случае переменной Numk присваивается порядковый номер текущей ступени, переменной Sk – величина текущей ступени и переменной Intk – значение времени, при котором имеет место переход на следующую ступень. Так как в конце последней ступени графика перехода не происходит, вне тела цикла присваиваются значения Numk, Sk и Intk для последней ступени. После этого, с использованием функции augment происходит формирование матрицы результатов выполнения программы, получаемой объединением вектор-столбцов переменных.
Для ввода нескольких строк программы, выполняемых по условию оператора if, следует поместить линию ввода, как показано на рис. 124– а, и нажать Add Line необходимое число раз(рис. 124– б).
| Рис. 124 |
| а) |
| б) |
Результат расчета программы Prog 2 заносится в одноименную матрицу, по столбцам представленную на рис. 125. Нулевой столбец содержит порядковый номер ступени упорядоченного сезонного графика, первый столбец – величину соответствующей ступени, второй столбец – время окончания ступени. Сравнив эти данные с графиком на рис. 122 нетрудно убедится, что расчет верен.
| Рис. 125 |
Важно! При реализации программы Prog 2 важным является выбор шага приращения времени в операторе цикла for. Если задать его слишком малым, то при расчете очередное значение времени может попасть на линии смены ступенек, которые не являются строго вертикальными. Это приведет к определению неверного числа ступеней, так как непосредственно на линии перехода от одной ступени к другой Sуп (t) также не равно Sуп (t +1). Проверка правильности выбора шага приращения времени осуществляется сравнением результата в нулевом столбце (см. рис. 125) с действительным числом ступеней на графике (см. рис. 122).
Нагрузочные потери по методу характерных суточных режимов рассчитываются по формуле:
,
а по методу времени наибольших потерь, если нагрузка задана графиком полной мощности, по формуле:
.
В исходных данных значения R и U не заданы, т.е. рассчитать величину потерь ни по одному из методов нельзя. Но, как следует из сравнения этих формул, при наличии возможности точного расчета эквивалентного времени наибольших потерь t, должно выполняться равенство:
.
Введем обозначения для столбцов матрицы, полученной в результате выполнения программы Prog 2, и рассчитаем величину квадратичной сезонной мощности (рис. 126). Обратите внимание на то, что в результате выполнения программы Prog 2 был сформирован столбец значений времени, при которых имеет место смена ступеней в упорядоченном графике нагрузки. Поэтому длительность первой ступени равна нулевому элементу вектора-столбца ENDstep, а длительности всех остальных ступеней вычисляются как разница времен окончания текущей и предыдущей ступени.
| Рис. 126 |
Выполним расчет 
, предварительно рассчитав величину времени наибольших потерь по формуле (54) через коэффициенты заполнения и формы графика активной нагрузки (рис. 126).
| Рис. 127 |
Как видно из результатов вычислений (см. рис. 126 и рис. 126), 
практически равно 
(5,551×108» 5,554×108).
Варианты индивидуальных заданий
| № | Индивидуальные данные | |||||||||||||||||||||||||
| Пример | Время | 0–1 | 1–2 | 2–3 | 3–4 | 4–5 | 5–6 | 6–7 | 7–8 | 8–9 | 9–10 | 10–11 | 11–12 | 12–13 | 13–14 | 14–15 | 15–16 | 16–17 | 17–18 | 18–19 | 19–20 | 20–21 | 21–22 | 22–23 | 23–24 | Рmax; Qmax |
| P | ||||||||||||||||||||||||||
| Q | Q = P× tg j, cos j = 0,85 | |||||||||||||||||||||||||
| 1. | P | |||||||||||||||||||||||||
| Q | ||||||||||||||||||||||||||
| 2. | P | |||||||||||||||||||||||||
| Q | ||||||||||||||||||||||||||
| 3. | P | |||||||||||||||||||||||||
| Q | ||||||||||||||||||||||||||
| 4. | P | |||||||||||||||||||||||||
| Q | ||||||||||||||||||||||||||
| 5. | P | |||||||||||||||||||||||||
| Q | ||||||||||||||||||||||||||
| 6. | P | |||||||||||||||||||||||||
| Q | ||||||||||||||||||||||||||
| 7. | P | |||||||||||||||||||||||||
| Q | ||||||||||||||||||||||||||
| 8. | P | |||||||||||||||||||||||||
| Q | ||||||||||||||||||||||||||
| 9. | P | |||||||||||||||||||||||||
| Q | Q = P× tg j, cos j = 0,95 |
| № | Индивидуальные данные | |||||||||||||||||||||||||
| 10. | Время | 0-1 | 1-2 | 2-3 | 3-4 | 4-5 | 5-6 | 6-7 | 7-8 | 8-9 | 9-10 | 10-11 | 11-12 | 12-13 | 13-14 | 14-15 | 15-16 | 16-17 | 17-18 | 18-19 | 19-20 | 20-21 | 21-22 | 22-23 | 23-24 | Рmax; Qmax |
| P | ||||||||||||||||||||||||||
| Q | ||||||||||||||||||||||||||
| 11. | P | |||||||||||||||||||||||||
| Q | Q = P× tg j, cos j = 0,8 | |||||||||||||||||||||||||
| 12. | P | |||||||||||||||||||||||||
| Q | ||||||||||||||||||||||||||
| 13. | P | |||||||||||||||||||||||||
| Q | ||||||||||||||||||||||||||
| 14. | P | |||||||||||||||||||||||||
| Q | Q = P× tg j, cos j = 0,67 | |||||||||||||||||||||||||
| 15. | P | |||||||||||||||||||||||||
| Q | ||||||||||||||||||||||||||
| 16. | P | |||||||||||||||||||||||||
| Q | ||||||||||||||||||||||||||
| 17. | P | |||||||||||||||||||||||||
| Q | ||||||||||||||||||||||||||
| 18. | P | |||||||||||||||||||||||||
| Q | ||||||||||||||||||||||||||
| 19. | P | |||||||||||||||||||||||||
| Q | ||||||||||||||||||||||||||
| 20. | P | |||||||||||||||||||||||||
| Q |
| № | Индивидуальные данные | |||||||||||||||||||||||||
| 21. | Время | 0-1 | 1-2 | 2-3 | 3-4 | 4-5 | 5-6 | 6-7 | 7-8 | 8-9 | 9-10 | 10-11 | 11-12 | 12-13 | 13-14 | 14-15 | 15-16 | 16-17 | 17-18 | 18-19 | 19-20 | 20-21 | 21-22 | 22-23 | 23-24 | Рmax; Qmax |
| P | ||||||||||||||||||||||||||
| Q | ||||||||||||||||||||||||||
| 22. | P | |||||||||||||||||||||||||
| Q | ||||||||||||||||||||||||||
| 23. | P | |||||||||||||||||||||||||
| Q | ||||||||||||||||||||||||||
| 24. | P | |||||||||||||||||||||||||
| Q | Q = P× tg j, cos j = 0,87 | |||||||||||||||||||||||||
| 25. | P | |||||||||||||||||||||||||
| Q | ||||||||||||||||||||||||||
| 26. | P | |||||||||||||||||||||||||
| Q | ||||||||||||||||||||||||||
| 27. | P | |||||||||||||||||||||||||
| Q | ||||||||||||||||||||||||||
| 28. | P | |||||||||||||||||||||||||
| Q |
Задания на защиту работы
Целью защиты лабораторной работы является проверка самостоятельности ее выполнения и понимания полученных результатов. В процессе защиты работы студент должен по заданию преподавателя продемонстрировать:
- понимание способов получения и назначения упорядоченных сезонных ступенчатых графиков нагрузки;
- понимание способов получения и назначения характерных суточных ступенчатых графиков нагрузки;
- знание разновидностей технических потерь в элементах сети передачи и распределения электроэнергии;
- знание методов расчета нагрузочных потерь, понимание условий применения и источников погрешностей каждого из методов;
- понимание физического смысла эквивалентного времени наибольших потерь;
- знание методов упорядочивания кусочных функций в MathCAD по убыванию и анализа упорядоченного графика с целью определения абсолютной величины и длительности ступеней графика;
- выполнение любого расчета хода выполнения работы для измененных исходных данных.
