Пример выполнения расчета по ходу выполнения работы
Рассмотрим пример выполнения работы для следующих исходных данных: Pmax =100 кВт; D t = 4 часа и заданного графика нагрузки (рис. 99).
| Рис. 99 |
Как отмечалось в разделе 2.4.4, форма непрерывных графиков нагрузки, полученной с использованием регистрирующих (самопишущих) приборов, может представлять значительные трудности для получения описания в виде аналитической функции. Чаще всего такие графики описывают с использованием кусочной сплайн-аппроксимации: рассматриваемое время разбивается на множество интервалов, и на каждом из них для описания фрагмента графика подбирается полином невысокого порядка (как правило, 3-го). Для упрощения анализа в данной работе рассматриваются простые примеры графиков нагрузки, подлежащие кусочной аппроксимации с использованием элементарных функций.
Как следует из анализа графика (см. рис. 99), можно выделить на рассматриваемом временном диапазоне (одни сутки) четыре временных интервала, в каждом из которых P (t) можно описать элементарной функцией. В интервале от 0 до 5 часов P (t) не изменяется и равна 20%; в интервале от 5 до 13 часов – возрастает по экспоненте, приближаясь к значению 80%; от 13 до 21 часа – убывает по экспоненте, приближаясь к значению 10%; от 21 до 24 часов – возрастает по экспоненте, приближаясь к значению 20%.
Возрастание произвольной функции f (t) по экспоненте на интервале времени от tнач до tкон описывается формулой вида:
 ,
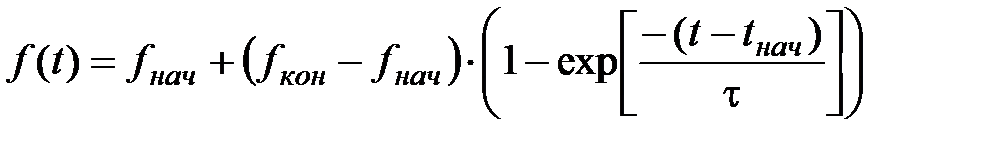| (93) |
где fнач и fкон – значения функции в моменты времени tнач и tкон соответственно; t – постоянная времени функции f (t), приближенно равная 1/3 интервала времени, за который значение функции достигает значения, равного 0,95× fкон. Так, по рис. 99 для интервала времени от tнач = 5 до tкон = 13 определяем: fнач = 20%; fкон = 80%; время достижения P (t) значения 0,95× fкон = 0,95×80 = 76 составляет приближенно 3 часа, т.е. t» 1 часу. Для интервала от 21 до 24 часов параметры определяются аналогично.
Убывание произвольной функции f (t) по экспоненте на интервале времени от tнач до tкон описывается формулой вида:
,
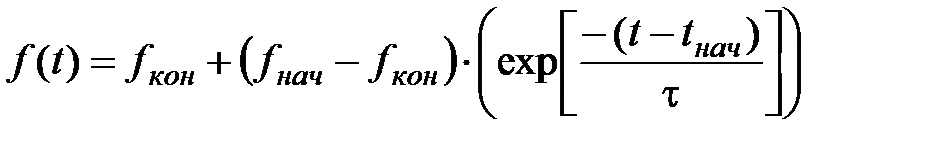где все значения констант аналогичны формуле (93), кроме t – для этой функции постоянная времени приближенно равна 1/3 интервала, за который значение функции достигает 1,05× fкон. Так, по рис. 99 для интервала времени от tнач = 13 до tкон = 21 определяем: fнач = 80%; fкон = 10%; время достижения P (t) значения 1,05× fкон = 1,05×10 = 10,5 составляет приближенно 3 часа, т.е. t» 1 часу.
По результатам анализа зададим в MathCAD четыре элементарные функции (рис. 100).
| Рис. 100 |
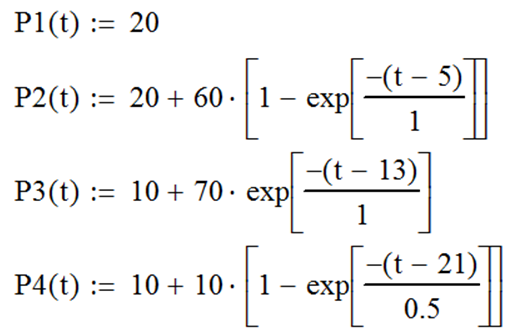
Для задания кусочной функции воспользуемся панелью семейства Programming (Программирование), которая вызывается кнопкой 
панели инструментов. Введем имя и оператор присваивания для функции P (t), после чего выберем оператор добавления строки программы Add Line в панели Programming (Программирование). Результат ввода будет иметь вид вертикальной черты с двумя позициями ввода для строк программы
(рис. 101– а). Для задания кусочной функции, состоящей из 4-х фрагментов, необходимо четыре позиции для ввода строк. Добавление строк осуществляется повторным нажатием Add Line нужное число раз (курсор при этом должен быть установлен как показано на рис. 101– а). Зададим вычисление элементарных функций на соответствующих интервалах времени с использованием оператора if панели Programming (Программирование) и операторов < и £ панели Boolean (Булева алгебра) как показано на
рис. 101– б.
| Рис. 101 |
| а) |
| б) |
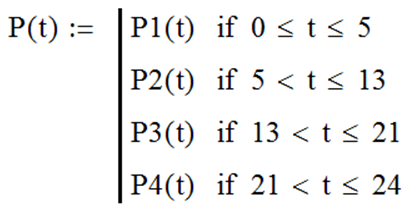
Важно! Не вводите оператора if набором с клавиатуры – только с использованием панели Programming (Программирование).
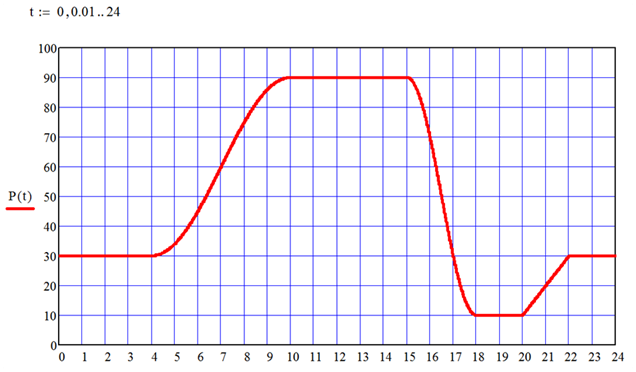
Результат построения графика заданной функции P (t) имеет вид, показанный на рис. 102. Как видно, он совпадет с исходными данными (см. рис. 99).
| Рис. 102 |
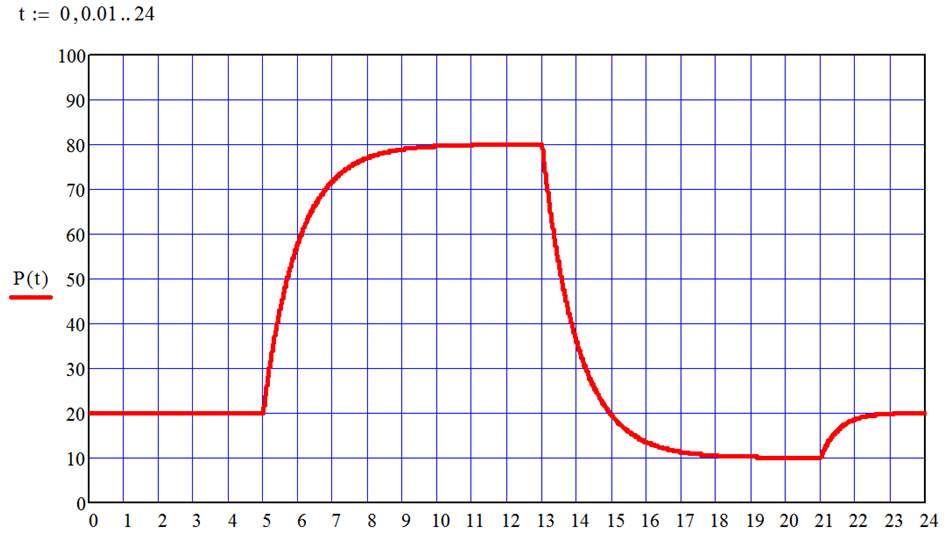
Введем заданное в исходных данных максимальное значение активной мощности нагрузки в абсолютных единицах и вычислим с использованием заданной кусочной функции P (t) количество электроэнергии, получаемой потребителем по формуле (37) за сутки как показано на рис. 103. Как видно, найденное значение составляет 885,009 кВт×ч.
| Рис. 103 |
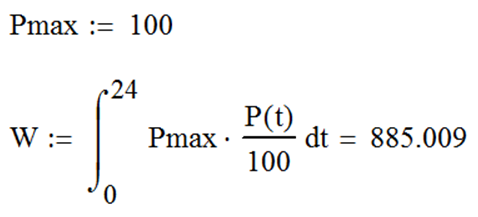
Для вычисления коэффициента неравномерности по формуле (39) необходимо определить максимальное и минимальное значение P (t) на интервале от 0 до 24 часов. Поиск аргументов функции y, при которых она принимает экстремальные значения, осуществляется с использованием встроенных функций MathCAD Minimize (y, x) и Maximize (y, x), рассмотренных в Работе №2. Для обеспечения точности анализа кусочной функции P (t), важно не только задать начальное приближение для аргумента t, но и ограничить диапазон поиска, определив его визуально по графику и задав в блоке Given как показано на рис. 104 (блоки вычисления t 1 и t 2 следует располагать один под одним).
| Рис. 104 |
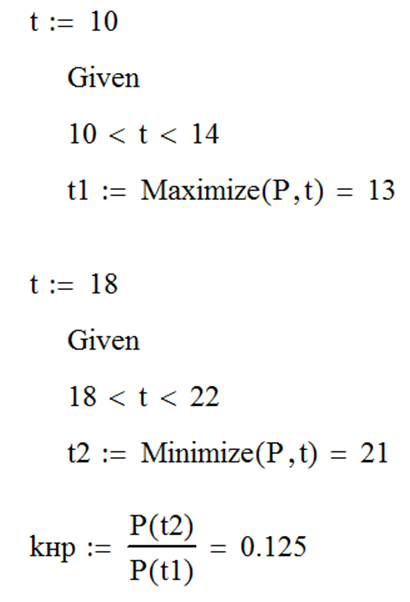
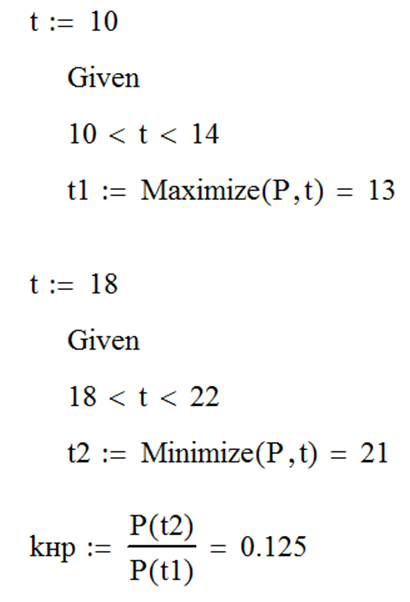
Заметим, что для рассматриваемого примера минимальное и максимальное значение функции P (t) очевидны, и для расчета kнр их достоверно можно определить по графику. К помощи расчета, показанного на рис. 104 следует прибегать в случае неочевидности значений.
Для вычисления коэффициентов заполнения формы необходимо по формулам (40) и (41) рассчитать среднюю и среднеквадратичную нагрузку (рис. 105).
| Рис. 105 |
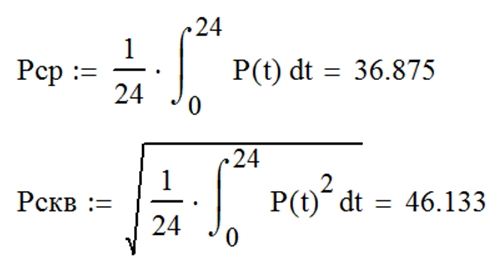
Коэффициенты заполнения и формы рассчитываются по формулам (42) и (43) соответственно (рис. 106).
| Рис. 106 |
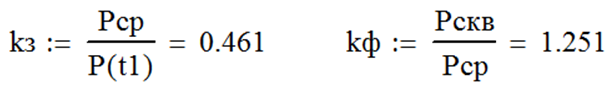
Как следует из результатов (см. рис. 104 и рис. 106), график нагрузки отличается существенной неравномерностью: kнр и kз значительно меньше единицы, а kф – больше.
По аналогии с годовым временем использования наибольшей нагрузки, рассчитываемым по формулам (45) и (47), определим данный параметр для суточного графика нагрузки через величину полученной потребителем электроэнергии и через коэффициент заполнения (рис. 107).
| Рис. 107 |
Как следует из результатов вычислений (см. рис. 107), суточная величина электроэнергии при работе с максимальной нагрузкой будет получена потребителем за 11,063 часа. Это также свидетельствует о существенной неравномерности графика нагрузки – tmax значительно меньше 24 часов.
Ступенчатые графики нагрузки строятся по показаниям счетчиков электроэнергии, взятых через равные промежутки времени. Точность графика, снятого по показаниям счетчика зависит от интервала отсчета D t, в пределах которого измеряемую составляющую нагрузки считают неизменной.
Будем считать, что в рассматриваемом примере результат измерения активной мощности в начале каждого интервала D t = 4 часа равен соответствующему значению непрерывного контроля P (t). Зададим с использованием операторов Add Line и if панели Programming (Программирование), и операторов сравнения панели Boolean (Булева алгебра) расчет дискретной (ступенчатой) функции Pст (t) как показано на рис. 108.
| Рис. 108 |
Важно! Функция Pст (t) должна иметь значение в момент времени t = 0, поэтому условие оператора if для P (0) записывается как показано в первой строчке программы вычисления на рис. 108. Кроме этого, функция очевидно должна иметь одинаковые значения в моменты времени t = 0 и t = 24, поэтому предпоследняя строчка программы вычисления на рис. 108 записана с использованием строго неравенства, а последняя – с использованием логического равенства (вводится с панели инструментов Boolean (Булева алгебра) или сочетанием клавиш Ctrl и =).
Результат построения графика заданной функции Pст (t) имеет вид, показанный на рис. 109. Как видно, он является достаточно грубым приближением непрерывного графика на рис. 102. Это объясняется большой величиной шага D t, используемой в расчете Pст (t).
| Рис. 109 |
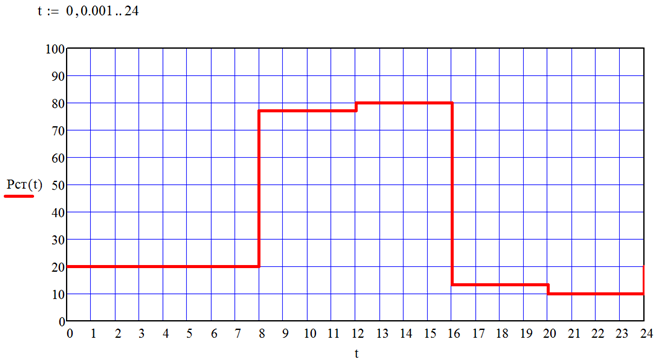
Важно! Обратите внимание на то, что несмотря на фиксированное приращение времени D t = 4 часа в расчете Pст (t), для построение графика этой функции шаг приращения аргумента задан равным 0,001 (см. рис. 102). Это вызвано необходимостью получить ступенчатую форму графика – при большой величине шага полученные точки будут соединены кратчайшими и получится кусочно-ломаная линия вместо ступенчатой. В средствах форматирования графиков MathCAD есть встроенный тип графика ступенчатого вида (закладка Трассировка, опция Тип / ступенька в окне редактирования свойств графика), при выборе которого шаг приращения можно выбрать равным D t. Однако для этого типа отсутствует возможность изменения толщины линии, что не всегда удобно с точки зрения наглядности результатов.
Расчет количества электроэнергии, получаемой потребителем за сутки, по ступенчатому графику Pст (t) выполняется по формуле (38) и в MathCAD при постоянной величине D t может быть реализован средствами автосуммирования двумя способами: с заданием вектора-столбца дискретных значений Pст (t) и вычислением суммы с использованием оператора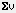 
Сумма вектора в панели инструментов Matrix (Матрица) как показано на рис. 110– а, или с использованием оператора 
Сумма в панели инструментов Calculus (Математический анализ) – см. рис. 110– б.
| Рис. 110 |
| а) |
| б) |
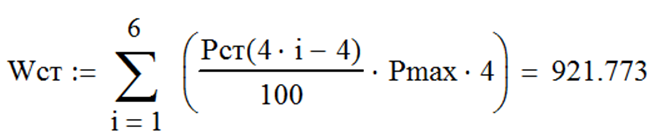
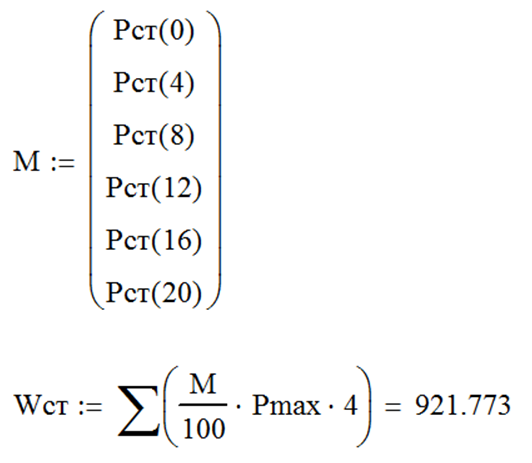
Как видно (см. рис. 110), результат приближенного расчета полученной электроэнергии с использованием ступенчатого графика нагрузки Pст (t) оказался завышенным в сравнении с точным значением, полученным по непрерывному графику P (t). Абсолютная и относительная погрешность приближенного расчета составляют, соответственно –36,764 кВт×ч и
–4,154% (рис. 111).
| Рис. 111 |
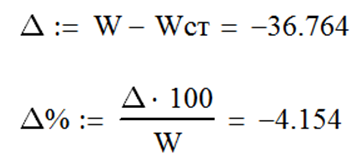
Дополнительные рекомендации по выполнению
индивидуальных вариантов
Кроме рассмотренных в примере выполнения работы элементарных функций, для задания непрерывного графика нагрузки могут быть использованы гармонические функции и линейные функции. Рассмотрим, например, график нагрузки, показанный на рис. 112.
| Рис. 112 |
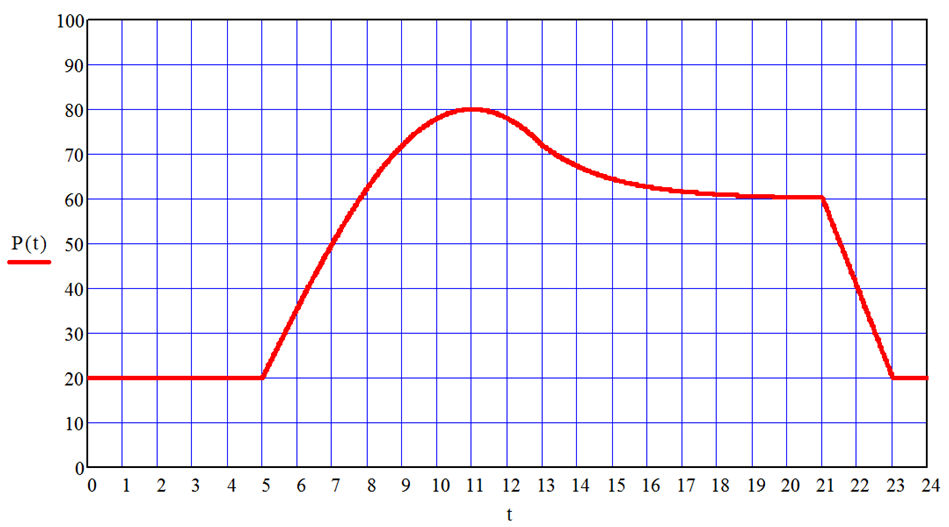
Как следует из анализа графика (см. рис. 112), можно выделить на рассматриваемом временном диапазоне (одни сутки) пять временных интервала, в каждом из которых P (t) можно описать элементарной функцией. В интервале от 0 до 5 часов P (t) не изменяется и равна 20%; в интервале от 5 до 13 часов – изменяется по синусоидальному закону; от 13 до 21 часа – убывает по экспоненте, приближаясь к значению 60%; от 21 до 23 часов – линейно убывает до 20% и в интервале от 23 до 24 часов не изменяется и равна 20%. Задание элементарных функций в соответствии с результатами анализа показано на рис. 113.
| Рис. 113 |
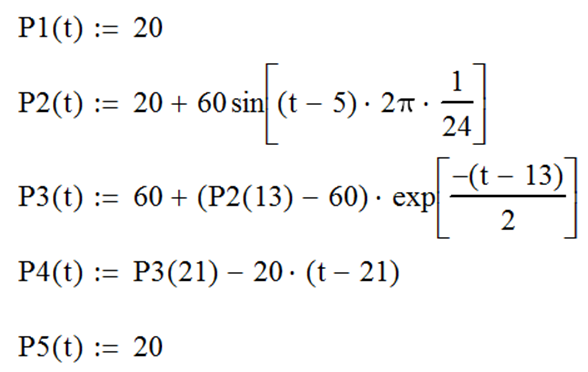
Функция Р 2(t) на рис. 113 задана с использованием формулы вида:
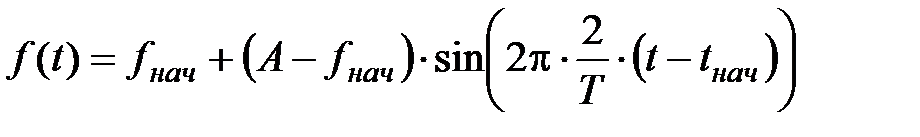
где fнач – значение функции в момент времени tнач; А – амплитудное значение; Т – период. Период легко определить по графику: как видно по
рис. 113 график достигает амплитудного значения (80%) за время, равное 11 – 5 = 6 часов, что составляет четверть периода, и значит Т = 4×6 = 24.
Линейная функция Р 4(t) на рис. 113 задана с использованием формулы вида:
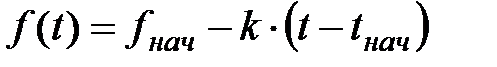
где fнач – значение функции в момент времени tнач; k – коэффициент линейной зависимости, который определяется по графику – видно, что за каждый час на интервале от 21 до 23 часов P (t) убывает на 20%.
Вычисление заданных функций на соответствующих интервалах времени с использованием оператора if панели Programming (Программирование) и операторов < и £ панели Boolean (Булева алгебра) показано на рис. 114.
| Рис. 114 |
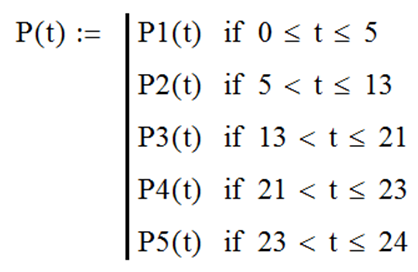
Еще один пример реализации расчета и построения непрерывного графика нагрузки показан на рис. 115 (вычислительные блоки, разделенные на рисунке вертикальной чертой с круглыми окончаниями, в рабочем листе MathCAD следует располагать один под одним).
| Рис. 115 |
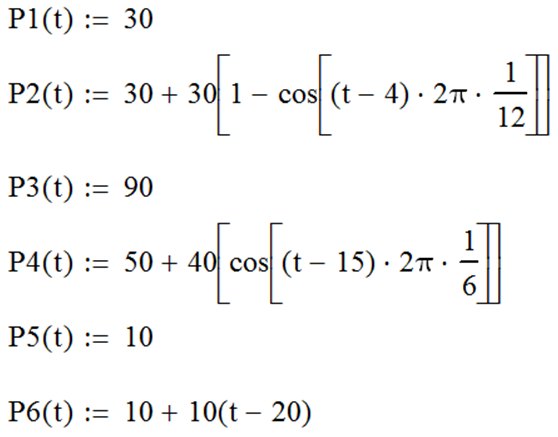
Варианты индивидуальных заданий
1. Рmax = 210 кВт; D t = 3 часа
2. Рmax = 110 кВт; t = 0, 5, 8, 10, 12, 15, 18, 21, 24 часа
3. Рmax = 80 кВт; D t = 2,4 часа
4. Рmax = 108 кВт; t = 0, 2, 6, 9, 12, 15, 18, 21, 24 часа
5. Рmax = 90 кВт; D t = 4 часа
6. Рmax = 380 кВт; t = 0, 3, 7, 10, 12, 14, 16, 19, 24 часа
7. Рmax = 180 кВт; D t = 2 часа
8. Рmax = 108 кВт; t = 0, 4, 9, 12, 15, 17, 20, 21, 24 часа
9. Рmax = 128 кВт; D t = 3 часа
10. Рmax = 201 кВт; t = 0, 4, 8, 12, 14, 17, 21, 22, 24 часа
11. Рmax = 284 кВт; D t = 2,4 часа
12. Рmax = 108 кВт; t = 0, 3, 7, 9, 12, 15, 18, 21, 24 часа
13. Рmax = 129 кВт; D t = 4 часа
14. Рmax = 580 кВт; t = 0, 1, 5, 8, 9, 12, 15, 21, 24 часа
15. Рmax = 338 кВт; D t = 2 часа
16. Рmax = 620 кВт; t = 0, 2, 6, 10, 12, 15, 19, 21, 24 часа
17. Рmax = 75 кВт; D t = 3 часа
18. Рmax = 245 кВт; t = 0, 4, 8, 10, 12, 15, 18, 22, 24 часа
19. Рmax = 800 кВт; D t = 2,4 часа
20. Рmax = 450 кВт; t = 0, 6, 9, 12, 15, 18, 22, 24 часа
21. Рmax = 490 кВт; D t = 4 часа
22. Рmax = 505 кВт; t = 0, 3, 7, 10, 14, 16, 21, 24 часа
23. Рmax = 260 кВт; D t = 2 часа
24. Рmax = 520 кВт; t = 0, 4, 8, 12, 15, 17, 20, 22, 24 часа
25. Рmax = 140 кВт; D t = 3 часа
26. Рmax = 95 кВт; t = 0, 4, 7, 9, 12, 14, 16, 18, 21, 24 часа
27. Рmax = 395 кВт; D t = 2,4 часа
28. Рmax = 225 кВт; t = 0, 5, 7, 9, 12, 15, 18, 21, 24 часа
Задания на защиту работы
Целью защиты лабораторной работы является проверка самостоятельности ее выполнения и понимания полученных результатов. В процессе защиты работы студент должен по заданию преподавателя продемонстрировать:
- понимание способов получения непрерывных и ступенчатых графиков нагрузки, знание разновидностей графиков нагрузки;
- знание способов расчета количества переданной потребителю электроэнергии по непрерывным и ступенчатым графикам нагрузки;
- понимание смысла параметров рассчитываемых по графикам нагрузки, умение объяснять зависимость величин этих параметров от формы графика нагрузки;
- знание методов задания кусочных функций в MathCAD и построения их графиков;
- выполнение любого расчета хода выполнения работы для измененных исходных данных и/или измененной формы математической модели статических характеристик нагрузки.
