Для выполнения работы понадобятся следующие панели MathCAD семейства Math (Математические):
- 
Graph (График): панель для вызова заготовок (форм) построения графиков;
- 
Matrix (Матрица): панель для ввода операторов создания, обращения, транспонирования матриц, операторы матричных индексов и столбцов, а также операторы для работы с векторами;
- Boolean (Булева алгебра): панель для задания логических операторов, а также знака логического равенства;
- 
Calculus (Математический анализ): панель для ввода операторов математического анализа: определенного и неопределенного интегралов, производных, пределов, сумм и произведений.
Для ввода исходных экспериментальных данных создадим матрицу с тремя столбцами и с количеством строк, равным числу экспериментальных точек. В первый столбец матрицы введем значения аргумента (относительная величина напряжения U / Uном), во второй и третий столбец – относительные значения активной и реактивной мощности нагрузки. Введем обозначения для столбцов матрицы (рис. 90).
| Рис. 90 |
Для вычисления коэффициентов полиномиальной регрессии вида y = f (x) в MathCAD используется встроенная функция regress (x, y, n), у которой последний аргумент n задает степень полинома. Функция regress формирует вектор, содержащий коэффициенты аппроксимирующего полинома.
Важно! Найденные коэффициенты располагаются в векторе, начиная с четвертого элемента в порядке возрастания степеней. Первые два элемента данного вектора являются служебными, третий равен коэффициенту полинома.
Пример задания функций regress для вычисления коэффициентов полиномов статических характеристик активной и реактивной составляющей нагрузки вида (91) и (92) и результат вычисления заданных функций показан на рис. 91.
| Рис. 91 |
Заметим, что в качестве аппроксимирующей функции для P (U) в данном примере выбрана линейная регрессия: последний аргумент функции coefficientР равен 1, т.е. уравнение (91) рассматривается для случая aP = 0. Если в индивидуальном варианте задана нелинейная форма модели для P (U), то степень этого полинома тоже должна быть равна 2.
С использованием найденных коэффициентов запишем окончательную форму математической модели расчета и анализа статических характеристик нагрузки для рассматриваемого примера:
 ;
|
|
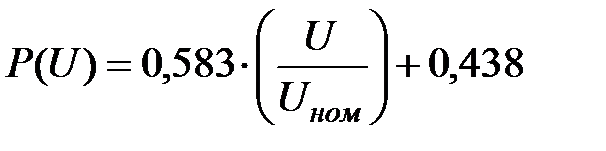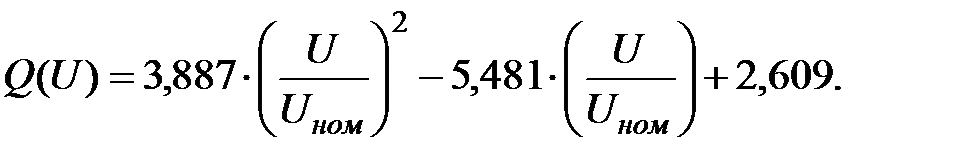
Для расчета полиномиальной регрессии, коэффициенты которой были вычислены с использованием функции regress (x, y, n), в MathCAD используется встроенная функция полиномиальной интерполяции interp (s, x, y, t), аргументы которой:
s = regress (x, y, k);
х – вектор-столбец заданных значений аргумента, элементы которого расположены в порядке возрастания;
у – вектор-столбец заданных значений функции того же размера;
t – значение аргумента полинома регрессии.
Зададим расчет полиномиальных функций статических характеристик как показано на рис. 92.
Важно! Обратите внимание на то, что заданный в примере на
рис. 92 аргумент полинома регрессии х это величина напряжения, которая в отличие от дискретных исходных данных в столбце U, является непрерывной и будет использована далее для построения графиков расчетных функций.
| Рис. 92 |
Построим графики экспериментальных и расчетных статических характеристик нагрузки. Расчетные статические характеристики Preg (x) и
Qreg (x) являются функциями непрерывного напряжения х, диапазон изменения которого для построения графика необходимо задать как показано на рис. 93. Для сравнения расчетных характеристик с экспериментальными данными вывод последних в поле построения графика задается как дискретные функции, значения Pi и Qi которых, а также общий аргумент Ui выбираются из соответствующих столбцов исходных данных по порядковому номеру i.
Важно! При задании в маркерах ввода поля построения графиков Pi, Qi и Ui используйте оператор индекс в панели Matrix (Матрица), который имеет вид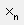 
.
| Рис. 93 |
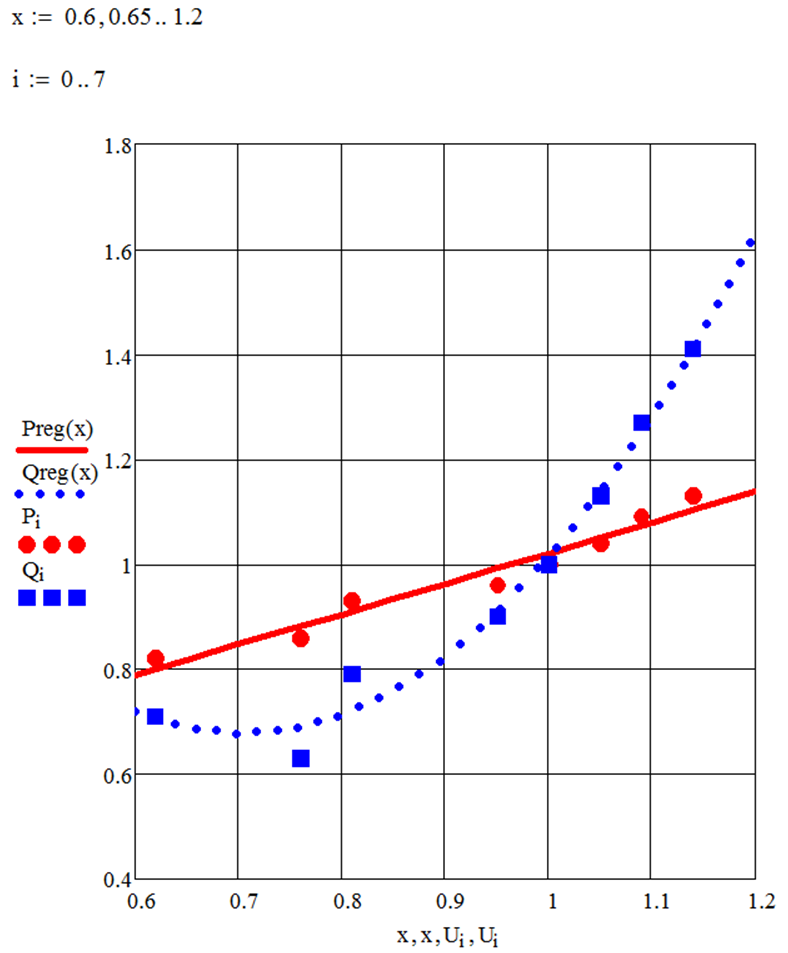
На рис. 93 линиями показаны расчетные графики статических характеристик, а отдельными маркерами-символами нанесены соответствующие экспериментальные данные. Как видно, расчетные характеристики достаточно точно описывают экспериментальные зависимости.
Для форматирования графиков указанным выше образом в окне Formatting Currently Selected X-Y Plot (Форматирование выбранного графика X-Y) следует выбрать закладку Трассировка и задать вывод первых двух графиков линиями разной гарнитуры, а двух последних, экспериментальных, – символами без соединительных линий, как показано на рис. 94. Выбор активизируется щелчком мыши по правой стороне соответствующей ячейки – при этом в ячейке появляется значок раскрывающегося списка.
| Рис. 94 |
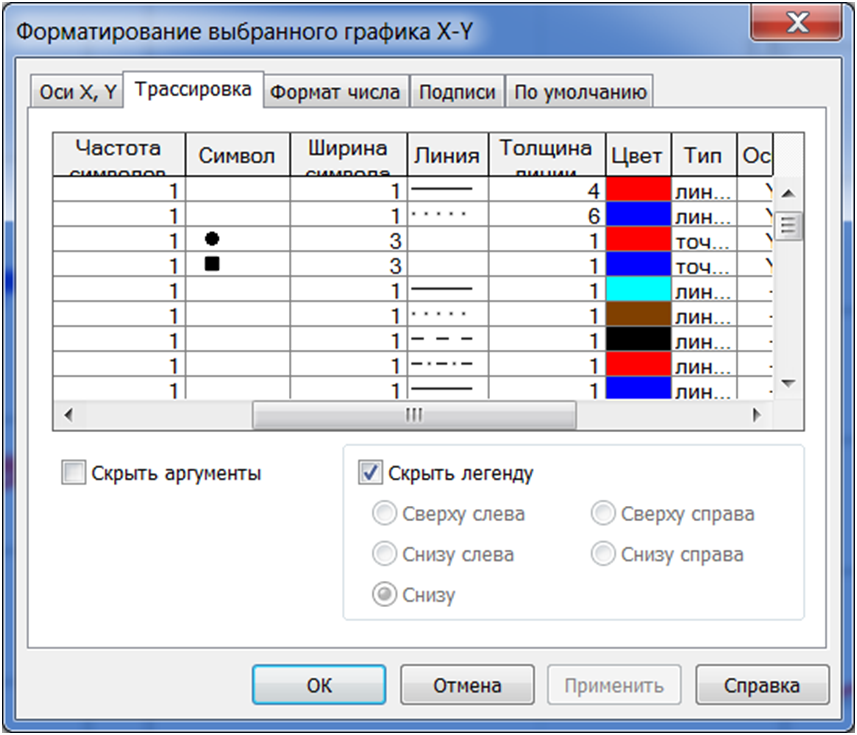
Зададим взятие производных от найденных расчетных функций статических характеристик и выполним расчет регулирующих эффектов нагрузки для некоторого значения напряжения, например, для номинального, т.е. для U / Uном = 1, воспользовавшись для задания производной соответствующим оператором панели Calculus (Математический анализ) как показано на рис. 95.
| Рис. 95 |
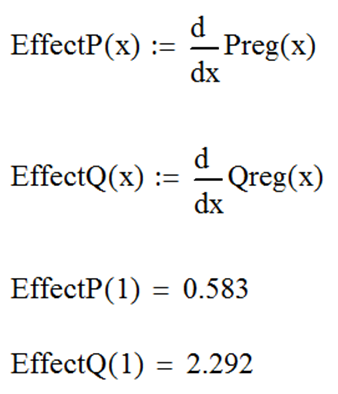
Как видно (см. рис. 95), при номинальном напряжении регулирующие эффекты активной и реактивной мощности являются положительными, и составляют, соответственно, 0,583 и 2,292.
Для определения величины критического напряжения Uкр по минимуму расчетной зависимости реактивной мощности от напряжения воспользуемся встроенной функцией Minimize (y, x), которая возвращает значение аргумента х, при котором ранее заданная функция y принимает минимальное значение. Для обеспечения поиска необходимо задать начальное приближение аргумента, определив его приблизительно по графику (рис. 96). Как следует из результата вычисления Uкр составляет 0,705 от Uном.
| Рис. 96 |
Построение зависимостей регулирующих эффектов нагрузки от напряжения показано на рис. 97. Как видно, регулирующий эффект активной мощности не меняется, т.к. модель этой статической характеристики была выбрана линейной. Регулирующий эффект реактивной мощности изменяется и меняет знак при величине напряжения, равной Uкр.
| Рис. 97 |
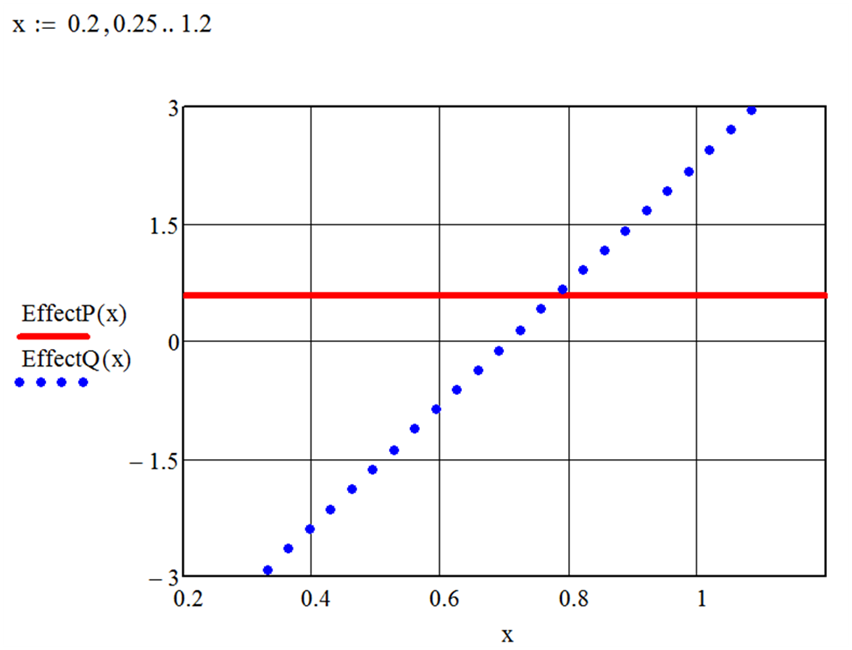
Для определения Uкр по функции регулирующего эффекта реактивной нагрузки необходимо определить точное значение аргумента, при котором функция принимает значение, равное 0 (происходит смена знака производной реактивной мощности по напряжению с «плюс» на «минус»).
Для решения уравнений в MathCAD используется специальный вычислительный блок Given-Find, который имеет следующую структуру:
- начальное приближение;
- вводное слово Given;
- уравнение, в котором качестве знака равенства нужно использовать логическое равенство (вводится с панели инструментов Boolean (Булева алгебра) или сочетанием клавиш Ctrl и =);
- функция Find (имя переменной), которая возвращает значение решения уравнения.
Определение Uкр по функции регулирующего эффекта реактивной нагрузки показано на рис. 98. Как видно, результат анализа совпадает со значением, ранее найденным по минимуму зависимости реактивной мощности от напряжения (0,705 от Uном).
| Рис. 98 |
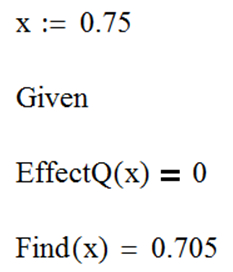
Варианты индивидуальных заданий
Условные обозначения в таблице исходных вариантов: Л – линейная форма модели P (U); Н – нелинейная форма модели P (U); РЭН – регулирующие эффекты нагрузки.
| № | Форма модели P (U) | Значение U / Uном для расчета РЭН | Экспериментальные данные, отн. ед. | № | Форма модели P (U) | Значение U / Uном для расчета РЭН | Экспериментальные данные, отн. ед. | ||||
| U | P | Q | U | P | Q | ||||||
| 1. | Л | 1,05 | 0,55 | 0,72 | 0,71 | 2. | Н | 0,90 | 0,52 | 0,82 | 0,71 |
| 0,72 | 0,8 | 0,6 | 0,68 | 0,86 | 0,63 | ||||||
| 0,85 | 0,9 | 0,62 | 0,85 | 0,93 | 0,79 | ||||||
| 0,95 | 0,94 | 0,79 | 0,95 | 0,96 | 0,9 | ||||||
| 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | ||||||
| 1,05 | 1,02 | 1,13 | 1,05 | 1,04 | 1,13 | ||||||
| 1,09 | 1,06 | 1,29 | 1,09 | 1,09 | 1,29 | ||||||
| 1,19 | 1,2 | 1,6 | 1,19 | 1,21 | 1,5 | ||||||
| 3. | Л | 0,92 | 0,55 | 0,75 | 0,71 | 4. | Н | 0,71 | 0,53 | 0,77 | 0,71 |
| 0,65 | 0,8 | 0,6 | 0,63 | 0,82 | 0,60 | ||||||
| 0,75 | 0,87 | 0,62 | 0,73 | 0,89 | 0,62 | ||||||
| 0,85 | 0,9 | 0,79 | 0,83 | 0,92 | 0,79 | ||||||
| 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | ||||||
| 1,05 | 1,09 | 1,13 | 1,03 | 1,11 | 1,13 | ||||||
| 1,15 | 1,2 | 1,4 | 1,13 | 1,22 | 1,40 | ||||||
| 1,25 | 1,4 | 1,8 | 1,23 | 1,42 | 1,80 | ||||||
| 5. | Л | 1,01 | 0,53 | 0,57 | 0,82 | 6. | Н | 1,11 | 0,57 | 0,69 | 0,97 |
| 0,63 | 0,71 | 0,54 | 0,67 | 0,71 | 0,86 | ||||||
| 0,76 | 0,85 | 0,62 | 0,73 | 0,85 | 0,73 | ||||||
| 0,87 | 1,00 | 0,79 | 0,89 | 0,98 | 0,85 | ||||||
| 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | ||||||
| 1,03 | 1,26 | 1,13 | 1,05 | 1,11 | 1,20 | ||||||
| 1,13 | 1,48 | 1,40 | 1,12 | 1,23 | 1,40 | ||||||
| 1,26 | 1,60 | 1,89 | 1,22 | 1,28 | 1,89 | ||||||
| 7. | Л | 0,67 | 0,54 | 0,76 | 0,86 | 8. | Н | 0,89 | 0,53 | 0,64 | 0,68 |
| 0,62 | 0,80 | 0,57 | 0,63 | 0,71 | 0,69 | ||||||
| 0,73 | 0,84 | 0,55 | 0,73 | 0,79 | 0,66 | ||||||
| 0,85 | 0,86 | 0,79 | 0,86 | 0,86 | 0,79 | ||||||
| 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | ||||||
| 0,94 | 0,98 | 0,91 | 0,94 | 0,88 | 0,91 | ||||||
| 1,05 | 1,04 | 1,20 | 1,12 | 1,11 | 1,20 | ||||||
| 1,16 | 1,06 | 1,34 | 1,20 | 1,21 | 1,34 | ||||||
| 9. | Л | 0,99 | 0,53 | 0,69 | 0,97 | 10. | Н | 1,09 | 0,57 | 0,69 | 1,04 |
| 0,63 | 0,71 | 0,86 | 0,65 | 0,71 | 0,86 | ||||||
| 0,76 | 0,85 | 0,73 | 0,81 | 0,94 | 0,73 | ||||||
| 0,87 | 0,98 | 0,85 | 0,89 | 0,98 | 0,85 | ||||||
| 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | ||||||
| 1,03 | 1,11 | 1,20 | 1,05 | 1,11 | 1,20 | ||||||
| 1,13 | 1,23 | 1,40 | 1,12 | 1,23 | 1,40 | ||||||
| 1,26 | 1,28 | 1,89 | 1,22 | 1,37 | 1,89 | ||||||
| 11. | Л | 1,10 | 0,53 | 0,64 | 0,73 | 12. | Н | 1,12 | 0,57 | 0,76 | 0,86 |
| 0,67 | 0,71 | 0,51 | 0,65 | 0,80 | 0,57 | ||||||
| 0,77 | 0,74 | 0,50 | 0,75 | 0,84 | 0,66 | ||||||
| 0,86 | 0,84 | 0,78 | 0,86 | 0,93 | 0,64 | ||||||
| 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | ||||||
| 0,95 | 0,91 | 0,76 | 0,93 | 0,98 | 0,91 | ||||||
| 1,12 | 1,16 | 1,36 | 1,08 | 1,11 | 1,20 | ||||||
| 1,22 | 1,21 | 1,48 | 1,14 | 1,13 | 1,34 | ||||||
| 13. | Л | 0,87 | 0,54 | 0,76 | 0,86 | 14. | Н | 0,93 | 0,53 | 0,64 | 0,86 |
| 0,62 | 0,80 | 0,57 | 0,67 | 0,71 | 0,61 | ||||||
| 0,80 | 0,84 | 0,55 | 0,77 | 0,79 | 0,60 | ||||||
| 0,85 | 0,93 | 0,64 | 0,86 | 0,84 | 0,58 | ||||||
| 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | ||||||
| 0,94 | 0,98 | 0,91 | 0,95 | 0,94 | 0,76 | ||||||
| 1,05 | 1,11 | 1,20 | 1,12 | 1,08 | 1,36 | ||||||
| 1,16 | 1,13 | 1,34 | 1,20 | 1,13 | 1,48 | ||||||
| 15. | Л | 0,75 | 0,56 | 0,64 | 0,73 | 16. | Н | 1,04 | 0,53 | 0,71 | 0,71 |
| 0,69 | 0,71 | 0,51 | 0,63 | 0,82 | 0,60 | ||||||
| 0,81 | 0,91 | 0,50 | 0,73 | 0,85 | 0,62 | ||||||
| 0,89 | 0,98 | 0,69 | 0,87 | 0,92 | 0,79 | ||||||
| 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | ||||||
| 1,05 | 1,11 | 1,20 | 1,03 | 1,11 | 1,13 | ||||||
| 1,12 | 1,16 | 1,36 | 1,13 | 1,22 | 1,40 | ||||||
| 1,22 | 1,21 | 1,66 | 1,26 | 1,42 | 1,89 | ||||||
| 17. | Л | 1,07 | 0,53 | 0,57 | 0,73 | 18. | Н | 1,00 | 0,60 | 0,69 | 0,87 |
| 0,63 | 0,71 | 0,60 | 0,69 | 0,71 | 0,75 | ||||||
| 0,76 | 0,85 | 0,73 | 0,81 | 0,98 | 0,75 | ||||||
| 0,87 | 1,06 | 0,70 | 0,89 | 0,98 | 0,92 | ||||||
| 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | ||||||
| 1,03 | 1,26 | 1,13 | 1,05 | 1,11 | 1,20 | ||||||
| 1,13 | 1,32 | 1,40 | 1,12 | 1,23 | 1,29 | ||||||
| 1,26 | 1,43 | 1,89 | 1,22 | 1,36 | 1,89 | ||||||
| 19. | Л | 0,84 | 0,56 | 0,69 | 0,87 | 20. | Н | 0,89 | 0,57 | 0,69 | 0,87 |
| 0,69 | 0,71 | 0,75 | 0,65 | 0,71 | 0,75 | ||||||
| 0,81 | 0,91 | 0,82 | 0,81 | 0,94 | 0,64 | ||||||
| 0,89 | 0,98 | 0,92 | 0,89 | 0,98 | 0,92 | ||||||
| 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | ||||||
| 1,05 | 1,11 | 1,04 | 1,05 | 1,11 | 1,20 | ||||||
| 1,12 | 1,23 | 1,36 | 1,12 | 1,23 | 1,40 | ||||||
| 1,22 | 1,36 | 1,89 | 1,22 | 1,26 | 1,89 | ||||||
| 21. | Л | 0,98 | 0,56 | 0,69 | 1,00 | 22. | Н | 0,79 | 0,53 | 0,64 | 0,86 |
| 0,69 | 0,71 | 0,75 | 0,67 | 0,71 | 0,61 | ||||||
| 0,81 | 0,91 | 0,67 | 0,77 | 0,79 | 0,60 | ||||||
| 0,89 | 0,98 | 0,80 | 0,86 | 0,84 | 0,72 | ||||||
| 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | ||||||
| 1,05 | 1,11 | 1,20 | 1,04 | 0,94 | 1,02 | ||||||
| 1,12 | 1,23 | 1,36 | 1,12 | 1,08 | 1,36 | ||||||
| 1,22 | 1,29 | 1,89 | 1,20 | 1,13 | 1,48 | ||||||
| 23. | Л | 1,10 | 0,59 | 0,64 | 0,73 | 24. | Н | 1,01 | 0,56 | 0,64 | 0,73 |
| 0,67 | 0,71 | 0,51 | 0,69 | 0,71 | 0,75 | ||||||
| 0,77 | 0,74 | 0,50 | 0,81 | 0,91 | 0,76 | ||||||
| 0,86 | 0,84 | 0,69 | 0,89 | 0,98 | 0,89 | ||||||
| 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | ||||||
| 0,95 | 0,91 | 0,86 | 1,05 | 1,11 | 1,20 | ||||||
| 1,12 | 1,16 | 1,36 | 1,12 | 1,23 | 1,36 | ||||||
| 1,22 | 1,21 | 1,66 | 1,22 | 1,29 | 1,66 | ||||||
| 25. | Л | 1,12 | 0,58 | 0,76 | 0,60 | 26. | Н | 0,82 | 0,53 | 0,64 | 0,86 |
| 0,68 | 0,80 | 0,57 | 0,63 | 0,71 | 0,61 | ||||||
| 0,73 | 0,84 | 0,55 | 0,73 | 0,79 | 0,60 | ||||||
| 0,84 | 0,86 | 0,79 | 0,86 | 0,84 | 0,72 | ||||||
| 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | ||||||
| 0,94 | 0,98 | 0,91 | 1,04 | 1,11 | 1,11 | ||||||
| 1,05 | 1,04 | 1,20 | 1,12 | 1,16 | 1,36 | ||||||
| 1,10 | 1,02 | 1,30 | 1,20 | 1,27 | 1,48 | ||||||
| 27. | Л | 1,075 | 0,54 | 0,76 | 0,69 | 28. | Н | 1,005 | 0,56 | 0,69 | 0,59 |
| 0,64 | 0,81 | 0,58 | 0,69 | 0,71 | 0,75 | ||||||
| 0,74 | 0,88 | 0,60 | 0,81 | 0,91 | 0,83 | ||||||
| 0,84 | 0,91 | 0,77 | 0,89 | 0,98 | 0,89 | ||||||
| 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | ||||||
| 1,04 | 1,1 | 1,11 | 1,05 | 1,11 | 1,20 | ||||||
| 1,14 | 1,21 | 1,38 | 1,12 | 1,23 | 1,36 | ||||||
| 1,24 | 1,41 | 1,78 | 1,22 | 1,29 | 1,52 |
Задания на защиту работы
Целью защиты лабораторной работы является проверка самостоятельности ее выполнения и понимания полученных результатов. В процессе защиты работы студент должен по заданию преподавателя продемонстрировать:
- понимание физического смысла статических характеристик нагрузки, умение объяснять зависимость формы этих характеристик от состава нагрузки;
- понимание физического смысла регулирующих эффектов нагрузки и причины изменения знака регулирующего эффекта реактивной составляющей нагрузки до и после критического значения напряжения;
- понимание сути методов регрессионного анализа, используемых в работе и умение обосновать вид полиномиальных функций математической модели статических характеристик нагрузки;
- выполнение любого расчета хода выполнения работы для измененных исходных данных и/или измененной формы математической модели статических характеристик нагрузки;
- построение графиков статических характеристик нагрузки заданием полиномиальных функций с использованием найденных значений коэффициентов регрессии.
