С использованием нестрогих итерационных методов, обеспечивающих получение удовлетворительного по точности результата за одну-две итерации, рассчитываются режимы простых замкнутых сетей. К простым замкнутым сетям относятся кольцевые сети (см. рис. 13) и сети с двусторонним питанием (см. рис. 14– а).
Кольцевая сеть содержит один контур, в одном узле которого расположен центр питания, а в других узлах – нагрузки. Принципиальная схема такой сети показана на рис. 47– а. Для расчета установившегося режима эта сеть условно разрезается по центру питания, развертывается и представляется в виде расчетной схемы замещения сети с двухсторонним питанием от источников А и В (рис. 47– б).
| Рис. 47 |
| а) |
| б) |
Исходными данными для расчета параметров режима являются, кроме параметров сети, следующие величины:
- напряжение центра питания, равное напряжениям источников А и В в расчетной схеме U 0 = UA = UВ;
- расчетные нагрузки узлов S 1, S 2,... Sn.
Требуется определить потокораспределение в кольцевой сети и напряжения в ее узлах 1, 2,... n.
Последовательность расчета кольцевой сети:
- определяется предварительное потокораспределение в сети без учета потерь мощности, при равенстве напряжений во всех узлах номинальному напряжению сети Uном;
- на основании предварительного потокораспределения определяется узел потокораздела и расчетная схема замещения кольцевой сети в этом узле делится на две разомкнутые схемы;
- для каждой из разомкнутых схем рассчитывается точное потокораспределение и напряжения в узлах с использованием методики расчета режима разомкнутой сети по напряжению, заданному начале сети (см. раздел 3.2.3).
Для определения предварительного потокораспределения зададимся произвольно направлениями мощностей (токов) в участках схемы замещения сети (рис. 48).
| Рис. 48 |
На основании второго закона Кирхгофа для замкнутого контура кольцевой сети запишем уравнение:
 .
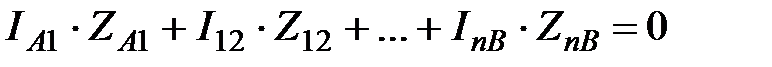| (72) |
Напомним, что значения тока и мощности связаны соотношениями:
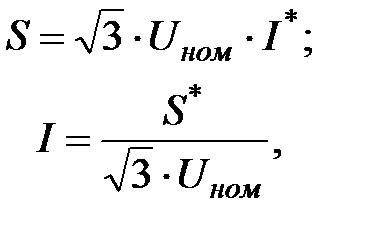
где I*, S* – сопряженные комплексы тока и мощности.
Перейдем в уравнении (72) от токов к мощностям:
 .
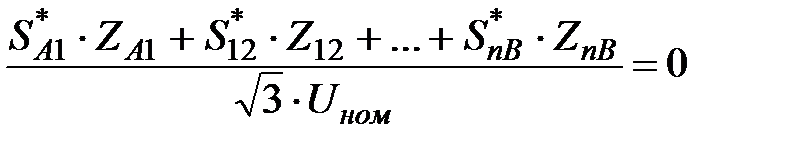| (73) |
После переноса сопряжения на комплексное сопротивление Z и умножения правой и левой части (73) на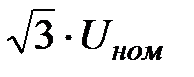 
получим:
 .
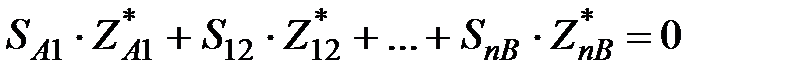| (74) |
На основании первого закона Кирхгофа для каждого из n узлов расчетной схемы замещения (см. рис. 48) можно записать:
 .
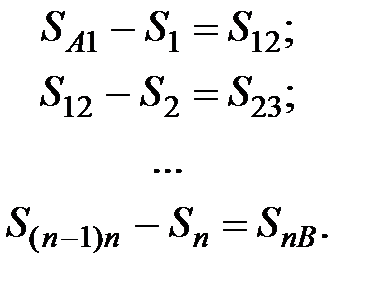| (75) |
Если объединить уравнения (74) и (75), то получим систему из (n +1) уравнений с (n +1) неизвестными SA 1, S 12, … S ( n -1) n, SnB. Решив эту систему относительно мощности головного участка сети SA 1, получим:
 ,
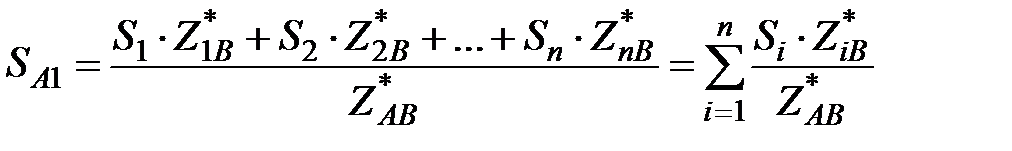| (76) |
где S i – расчетная нагрузка i -того узла;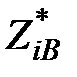 
– сумма сопряженных комплексов сопротивлений участков ЛЭП между узлами i и В; 
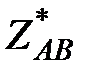– сумма сопряженных комплексов сопротивлений всех участков ЛЭП (от источника А до источника В).
Аналогично можно получить выражение для мощности SnB второго головного участка сети:
 ,
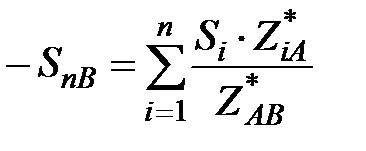| (77) |
где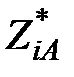 
– сумма сопряженных комплексов сопротивлений участков ЛЭП между узлами i и А. Знак «минус» в выражении (77) означает, что мощность течет от узла B к узлу n, т.е. – SnB = SBn.
Как следует из выражений (76) и (77), поток мощности на головном участке замкнутой сети равен сумме произведений нагрузки каждого узла на сопряженное сопротивление сети от этого узла до противоположного источника питания, поделенной на сопряженное суммарное сопротивление всей сети.
После определения мощностей головных участков потоки мощности на остальных участках электрической сети однозначно определятся по уравнениям первого закона Кирхгофа (75). Значения части мощностей участков получатся отрицательными. Это означает, что они имеют обратное направление по отношению к изначально принятому (см. рис. 48). Т.о., в результате выполнения расчетов по выражениям (74)…(77) получится, что к некоторому узлу i мощности поступают с двух сторон. Такой узел называется узлом потокораздела и обозначается на схемах значком ▼
(рис. 49– а). После определения узла потокораздела расчетная схема замещения преобразовывается к виду, приведенному на рис. 49– б, т.е. условно разрезается в узле потокораздела на две разомкнутые схемы. Расчетные нагрузки узлов i' и i'' левой и правой частей схемы равны найденным мощностям, поступающим к узлу потокораздела: Si' = S ( i -1) i, S i'' = S ( i +1) i. Расчетные нагрузки остальных узлов те же самые, что и в исходной схеме.
| Рис. 49 |
| а) |
| б) |
Т.о., в результате всех предшествующих расчетов исходная кольцевая сеть приведена к двум разомкнутым схемам замещения с известными расчетными нагрузками узлов и напряжениями источников питания – UA и UB (см. рис. 49– б), равными напряжению центра питания исходной кольцевой схемы U 0. Дальнейший расчет параметров режима этих двух схем замещения выполняется с использованием методики расчета режима разомкнутой сети по напряжению, заданному начале сети (см. раздел 3.2.3).
Выполним анализ потокораспределения в промежуточной замкнутой сети (рис. 49– а). Раскрывая полные мощности и сопротивления в выражении (76), получим:
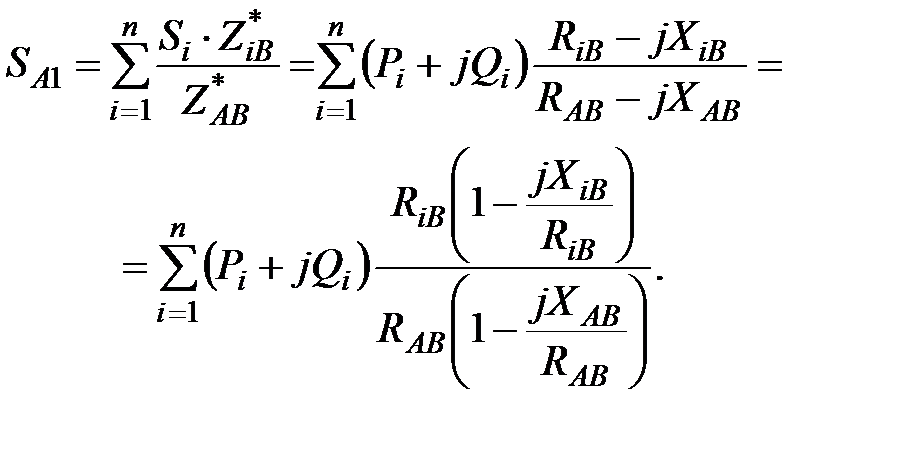
| (78) |
Если в замкнутой сети имеет место постоянное соотношение реактивных и активных сопротивлений Х / R = const, то расчет потокораспределения можно выполнять с учетом только активных сопротивлений, поскольку в этом случае (1– jXiВ / RiВ) = (1– jXАВ / RАВ), и формула (78) принимает вид:
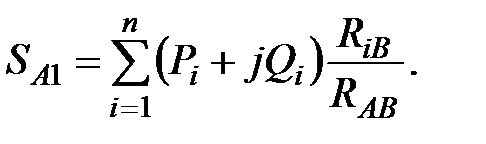
| (79) |
Аналогичные изменения претерпевает при Х / R = const и формула (77) для расчета мощности SnB второго головного участка сети.
Замкнутая сеть, в которой для всех ее участков выполняется соотношение Х / R = const, называется однородной. Такой сетью, в частности, будет кольцевая сеть, выполненная воздушными линиями одинакового сечения или кабельными линиями одинакового сечения. И в том, и в другом случае сеть должна быть одного напряжения, без трансформации в узлах нагрузки.
Запишем (79) в виде:
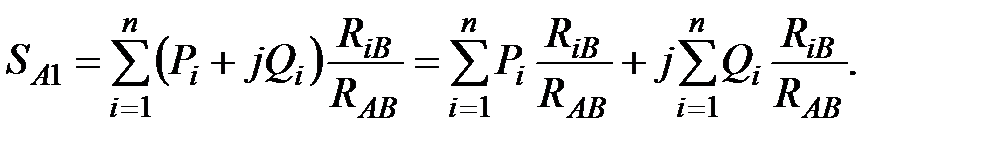
| (80) |
Как следует из (80), в однородной замкнутой сети потокораспределение можно рассчитывать отдельно для активных и реактивных мощностей. В этом случае рассчитываются две независимые замкнутые схемы. Первая имеет только активные нагрузки, вторая – реактивные. В первой схеме определяется потокораспределение активных мощностей, во второй – реактивных мощностей. Такой прием, называемый расщеплением сети, уменьшает трудоемкость расчетов, так как эти расчеты ведутся для действительных, а не комплексных величин.
Если замкнутая сеть выполнена воздушными линиями с проводами различных сечений или воздушными и кабельными линиями, то для различных ее участков соотношение Х / R ≠ const и такая сеть будет неоднородной.
Если замкнутая сеть выполнена линиями различного номинального напряжения, т.е. кроме участков ЛЭП элементами этой сети являются трансформаторы, то такая сеть будет иметь сильную степень неоднородности, поскольку отношение Х / R для трансформаторов значительно больше отношения Х / R для воздушных или кабельных линий.
В неоднородной сети по замкнутому контуру циркулирует уравнительная мощность, равная разности мощностей, определяемых выражениями (76) и (79):
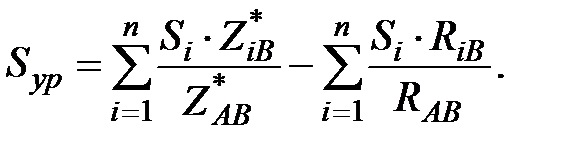
| (81) |
Уравнительная мощность, обусловленная неоднородностью сети и протекающая по всем ее элементам, вызывает дополнительные потери активной мощности в сети. Чем больше степень неоднородности замкнутой сети, тем больше величина уравнительной мощности и тем больше величина дополнительных потерь мощности.
Для уменьшения потерь мощности в неоднородной замкнутой сети потокораспределение в ней стремятся приблизить к потокораспределению, соответствующему однородной замкнутой сети. Для этого применяют специальные меры принудительного изменения потокораспределения в неоднородной сети.
Сеть с двухсторонним питанием (см. рис. 14– а) может иметь в общем случае отличающиеся напряжения центров питания, т.е. в представлении ее расчетной схемой замещения вида, показанного на рис. 47– б, напряжения источников питания UA ¹ UВ. В этом случае, даже при Х / R = const по сети потечет уравнительный ток:
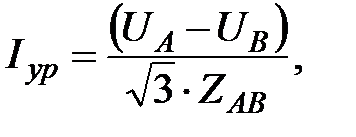
или уравнительная мощность:
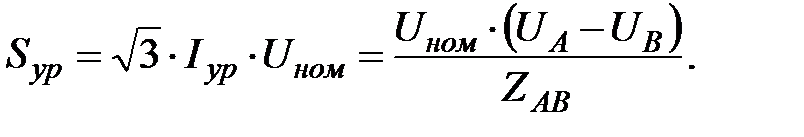
Расчет такой сети выполняется с использованием метода наложения. Сначала определяется потокораспределение в схеме при равенстве напряжений источников UА = UВ как в методике расчета кольцевой сети. Действительные потоки мощности в линиях сети определятся суммированием мощностей, полученных при условии UА = UВ, с уравнительной мощностью Sур [9, 10, 19, 24].
