Рассмотрим методы расчета режима при заданной мощности нагрузки для случаев, когда напряжение задано в конце ЛЭП и когда напряжение задано в начале ЛЭП (на источнике питания).
3.2.1. Расчетные нагрузки узлов электрической сети
Как уже отмечалось в разделе 3.1, в числе прочих исходных данных для расчета режимов необходима схема замещения сети. Для упрощения расчетных схем с номинальным напряжением до 220 кВ вводят понятие расчетной нагрузки. Рассмотрим для примера фрагмент схемы районной электрической сети, включающей два участка воздушной ЛЭП W 1 и W 2, сходящиеся в узле 1 (рис. 40). К узлу подключен трансформатор с нагрузкой, заданной неизменной мощностью Sн 1 = Рн 1 + jQн 1 на шинах низшего напряжения трансформатора.
| Рис. 40 |
На рис. 41 показана схема замещения этой сети, составленная из схем замещения участков ЛЭП и трансформатора. Для замещения участков ЛЭП использована модификация схемы вида, показанного на рис. 25– в (без учета потерь на корону, несущественных в воздушных линиях до 220 кВ). В этой модификации в поперечной ветви вместо составляющих показано полное сопротивление ЛЭП и вместо двух поперечных ветвей с емкостными проводимостями показаны поперечные ветви, учитывающие зарядную мощность ЛЭП. Способ отображения поперечной ветви со стрелкой, направленной к продольной ветви, показанный на рис. 41, определяется тем, что ЛЭП с поперечной емкостной проводимостью, потребляющая из сети опережающий напряжение емкостной ток, является источником реактивной (зарядной) мощности. Для замещения трансформатора использована схема замещения вида, показанного на рис. 26– в, у которой в продольной ветви показано полное сопротивление трансформатора, а в поперечной – полная мощность потерь холостого хода.
| Рис. 41 |
Можно упростить схему замещения, показанную на рис. 41, определив расчетную нагрузку узла 1 следующим образом:
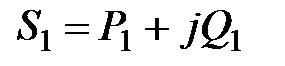 ; ;
 ; ;
 , ,
| (55) |
где D РТ и D QТ – суммарные потери мощности в трансформаторе (потери в обмотках трансформатора, т.е. в сопротивлении ZТ и потери холостого хода); QC 1и QC 2 – зарядные мощности участков ЛЭП W 1 и W 2. Суммарные потери активной и реактивной мощности в трансформаторе при его нагрузке, равной Sн 1 составляют:
 , ,  . .
| (56) |
Зарядные мощности линий QC 1и QC 2 рассчитываются по формуле (15).
Найденная велична S 1 иногда называется расчетной мощностью подстанции. Ее вычисление предшествует расчету режима сети, а т.к. напряжения в узлах схемы замещения в начале расчета неизвестны, то слагаемые расчетной мощности рассчитываются по приближенным формулам (56) и (15) с использованием номинального напряжения сети.
После определения расчетной нагрузки узла 1 по формулам (55) схема замещения сводится к виду, приведенному на рис. 42. Как видно в сравнении с рис. 41, часть схемы, соответствующая узлу 1, заметно упростилась. Найденная мощность S 1 отражает влияние зарядных мощностей линии и потерь мощности в трансформаторе на режим ветвей расчетной схемы, примыкающей к трансформатору, и на режим всей сети. Аналогично определяются расчетные нагрузки узлов, к которым подходят три и более линий [10, 21].
| Рис. 42 |
3.2.2. Расчет режима разомкнутой сети по напряжению,
заданному в конце сети
Рассмотрим задачу в общей постановке применительно к магистральной схеме разомкнутой сети на n потребителей, показанной на рис. 43.
| Рис. 43 |
По условию заданы мощности нагрузок Sн 1… Sнn, сопротивления и проводимости участков ЛЭП, и напряжение в конце последнего участка Un (напряжение в узле n).
Расчет режима заключается в последовательном определении от конца ЛЭП к ее началу неизвестных мощностей во всех ветвях схемы, включая мощность источника питания S 0, и напряжений во всех узлах, включая напряжение источника питания U 0.
Как уже отмечалось в разделе 3.2.1, расчету режима предшествует определение расчетных нагрузок узлов сети и приведение схемы замещения сети к виду, показанному на рис. 44. На рисунке индексом «н» отмечены мощности в начале каждого участка ЛЭП, а индексом «к» – мощность в конце каждого участка.
| Рис. 44 |
В результате определения расчетных нагрузок мощность в конце
n -го участка известна:
 .
.
В этом случае расчет установившегося режима электрической сети выполняется прямым методом с использованием закона Ома и первого закона Кирхгофа. Мощность в начале n -го участка линии отличается от мощности в ее конце на величину потерь:
 ; ;
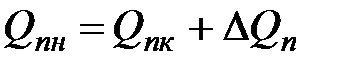 . .
| (57) |
Потери мощности в n -м участке линии составляют:
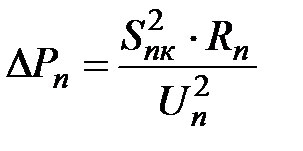 ; ;
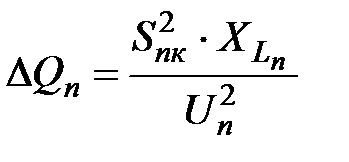 . .
| (58) |
Напряжение в узле (n –1) отличается от напряжения в узле n на величину падения напряжения в n -м участке линии:
 . .
| (59) |
Падение напряжения в n -м участке линии в соответствии с законом Ома составляет:
 . .
| (60) |
Мощность в конце (n –1)-го участка линии определится по первому закону Кирхгофа с учетом расчетной нагрузки узла (n –1):
 ; ;
 ; ;
 . .
| (61) |
Далее расчет повторяется с использованием формул (57)…(61). Эти формулы, записанные для n -го участка линии, справедливы для любого
i -го участка, если в них вместо индекса n подставить индекс i. В завершение расчета мощность, поступающая в сеть от источника питания с учетом зарядной мощности начала 1-го участка линии, не вошедшей в расчетную нагрузку узла, определится как:
 ; ;
 ; ;
 . .
| (62) |
Заметим, что при движении от конца схемы к ее началу напряжение от узла к узлу меняется как по величине, так и по фазе [9, 10, 21].
3.2.3. Расчет режима разомкнутой сети по напряжению,
заданному в начале сети
При расчетах установившихся режимов районных электрических сетей напряжение, как правило, задается в центре питания этой сети. Применительно к схеме замещения (см. рис. 44), кроме параметров сети, считаются заданными:
- напряжение источника U 0;
- расчетные нагрузки узлов S 1, S 2,... Sn.
Требуется определить:
- напряжения в узлах U 1, U 2,... Un электрической сети;
- потокораспределение в ветвях схемы: мощности в начале (S 1 н , S 2 н ,... Snн) и конце (S 1 к , S 2 к ,... Snк) каждого участка ЛЭП, включая мощность источника питания S 0.
В рассматриваемом случае, в отличие от предыдущего (см. раздел 3.2.2.), применение прямого метода невозможно. В этом случае используется итерационный метод расчета. Каждая итерация состоит из двух этапов, рассматриваемых ниже.
Первый этап (прямой ход) начинается с того, что для всех n узлов электрической сети задаются начальные приближения напряжений, равные номинальному напряжению сети Uном. Далее по выражениям, аналогичным (58), для n -го участка линии, с учетом того, что  , определяются потери мощности:
, определяются потери мощности:
 ; ;
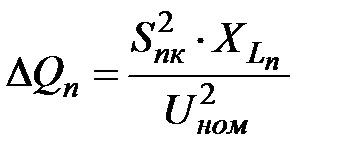 . .
| (63) |
Далее рассчитывается мощность в начале n -го участка линии, которая отличается от мощности в ее конце на величину потерь:
 ; ;
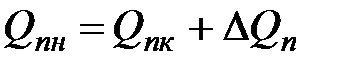 . .
| (64) |
Мощность в конце (n –1)-го участка линии определится по первому закону Кирхгофа с учетом расчетной нагрузки узла (n –1):
 ; ;
 ; ;
 . .
| (65) |
Далее расчет повторяется с использованием формул (63)…(65) до определения мощности S 1 н в начале 1-ой линии. Эти формулы, записанные для n -го участка линии, справедливы для любого i -го участка, если в них вместо индекса n подставить индекс i. В завершение расчета мощность, поступающая в сеть от источника питания с учетом зарядной мощности начала 1-го участка линии, не вошедшей в расчетную нагрузку узла, определяется по формуле (62).
После определения мощностей в конце и начале каждого i -того участка линии и мощности источника питания первый этап расчета заканчивается.
На втором этапе (обратный ход) по заданному напряжению источника питания U 0 и полученному на первом этапе потокораспределению определяются напряжения в узлах 1, 2,... n электрической сети. Так, например, напряжение в узле 1 составит:
 . .
| (66) |
Падение напряжения в1-ом участке линии выразим через ток I 1 и мощность в начале участка S 1 н :
 . .
| (67) |
Аналогично, напряжение в произвольном i -том узле:
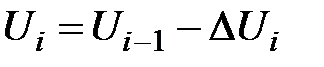 , ,
 . .
| (68) |
Определением напряжений в узловых точках электрической сети заканчивается второй этап первой итерации.
На второй итерации вновь рассчитывается потокораспределение в сети, но при этом используются уже не номинальные напряжения, а найденные на первой итерации напряжения в узлах. Затем по полученному потокораспределению уточняются напряжения в узлах. Количество итераций определяется требуемой точностью расчета. При расчетах установившихся режимов разомкнутых районных электрических сетей, как правило, достаточно одной–двух итераций [10, 19, 21].
3.2.4. Расчет напряжения на вторичной обмотке трансформатора
В рассмотренных выше расчетах установившихся режимов районных электрических сетей определялись напряжения в узлах, соответствующие напряжениям на первичной обмотке трансформаторов подстанций. Для определения действительного напряжения на вторичной обмотке трансформаторов рассмотрим произвольный i -тый узел электрической сети (рис. 45– а) и схему замещения фрагмента понижающей подстанции (рис. 45– б).
| Рис. 45 |
| а) |
| б) |
Нагрузка подстанции (см. рис. 45– а) Sнi задана на шинах вторичного напряжения трансформатора. В результате расчета установившегося режима электрической сети известно напряжение Ui на первичной обмотке трансформатора. Необходимо определить действительное напряжение на вторичной обмотке трансформатора Ui ’’. Такой расчет необходим для оценки величины этого напряжения и необходимости его регулирования с целью обеспечения требуемого качества электроэнергии у потребителей.
В схеме замещения (рис. 45– б) трансформатор представлен Г–образной схемой замещения (∆ Sx, ZТ) и идеальным трансформатором (трансформатором без потерь мощности) с коэффициентом трансформации:
 ,
,
где Uвн, Uнн – номинальные напряжения первичной и вторичной обмоток
трансформатора.
Расчет действительного напряжения на вторичной обмотке трансформатора выполняется в следующей последовательности. Определяется величина падения напряжения в трансформаторе:
 . .
| (69) |
В формуле (69) используется номинальное напряжение сети Uном, поскольку нагрузка задана на шинах вторичного напряжения трансформатора, а напряжение известно на его первичной обмотке.
Напряжение на вторичной обмотке трансформатора, приведенное к первичному напряжению, составляет:
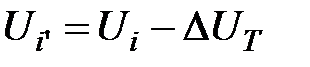 . .
| (70) |
Действительная величина напряжения на вторичной обмотке трансформатора определяется, с учетом коэффициента трансформации kТ, по выражению:
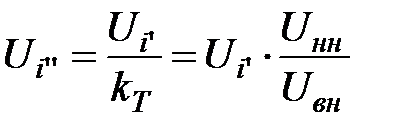 . .
| (71) |
По величине напряжения Ui ’’ оценивают необходимость его регулирования [10, 19].
3.2.5. Особенности расчета местных электрических сетей
Местные распределительные сети включают в себя воздушные линии напряжением до 35 кВ включительно. Такие сети выполняются, как правило, разомкнутыми. Рассмотренные выше методы расчета районных распределительных сетей напряжением до 220 кВ справедливы и для расчета местных электрических сетей. Однако в силу специфики местных сетей, а именно меньших напряжений и меньших длин линий электропередачи чем у районных сетей, для расчета местных сетей принимают ряд упрощающих допущений:
- в ЛЭП не учитывается емкостная проводимость и, следовательно, зарядная мощность (схемы замещения – в соответствии с рис. 25– а, б), в трансформаторах не учитываются потери холостого хода ∆ Рх и ∆ Qx –схемы замещения элементов местной электрической сети содержат только продольные активные и реактивные сопротивления;
- потокораспределение в местной электрической сети рассчитывается без учета потерь мощности в ее элементах. Это потокораспределение обусловлено только величинами нагрузок в узлах электрической сети, а мощности в начале и конце каждой линии сети принимаются равными между собой. Мощность, протекающая по любой линии местной сети, равна сумме нагрузок, расположенных в конце этой линии и далее в сторону, противоположную центру питания;
- при расчете местной сети пренебрегают поперечной составляющей падения напряжения в линиях электропередачи и трансформаторах, и рассчитывают только продольную.
Для примера схемы разветвленной местной электросети (рис. 46) мощность, протекающая, например, по линии между узлами 2 и 3 равна:
S 23 = S 3 + S 4 + S 5 + S 6 + S 7 + S 8.
Потоки мощности в других линиях определяются аналогично.
| Рис. 46 |
Продольная составляющая падения напряжения в линии между узлами i и j определяется как:
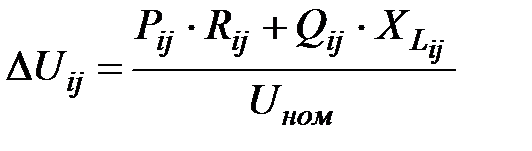 .
.
Эта продольная составляющая падения напряжения, приблизительно равная алгебраической разности напряжений в начале и конце линии, называется потерей напряжения.
Потерю напряжения в линиях и трансформаторах местной электрической сети выражают, как правило, в процентах или долях от номинального напряжения сети Uном.
Достаточно жесткие требования к качеству электроэнергии со стороны потребителей в местных электрических сетях ограничивают наибольшую потерю напряжения ∆ Umax в этих сетях величиной допустимой потери напряжения ∆ Uдоп = 0,06× Uном. Наибольшая потеря напряжения есть алгебраическая разность между напряжением в центре питания (ЦП) местной сети и узлом сети с самым низким напряжением.
Для определения наибольшей потери напряжения в разветвленной местной электрической сети рассчитываются суммарные потери напряжения ∆ U Σ k от ЦП до каждого k -того конечного (тупикового) потребителя, из полученных значений выбирается наибольшее значение (∆ Umax), которое сравнивается с допустимой потерей.
Для схемы на рис. 46 k = 5, 8, 10, и суммарные потери напряжения от ЦП до узлов 5, 8 и 10 составляют:
∆ U Σ5 = ∆ U ЦП,1 + ∆ U 12 + ∆ U 23 + ∆ U 34 + ∆ U 45;
∆ U Σ8 = ∆ U ЦП,1 + ∆ U 12 + ∆ U 23 + ∆ U 36 + ∆ U 67 + ∆ U 78;
∆ U Σ10 = ∆ U ЦП,1 + ∆ U 19 + ∆ U 9,10.
Из найденных значений ∆ U Σ5, ∆ U Σ8, и ∆ U Σ10 выбирается максимальное, принимается за ∆ Umax и сравнивается с допустимой потерей напряжения ∆ Uдоп = 0,06× Uном [10, 19, 21].






