Отображение Вейля представляет собой билинейное отображение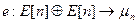 
, обладающее следующими свойствами:
• (билинейность) 
• e(P,P) = 1 для любого P ∈ E[n],
• (невырожденность) (∃P, Q ∈ E[n]) 
,
• (вычислимость) e(X,Y) может быть эффективно вычислено.
Если степень вложения k принимает небольшие значения (до k = 6), то для поиска ключа шифрования вместо решения задачи ДЛЭК можно решать более легкую задачу вычисления дискретного логарифма в конечном поле размерности qk. Таким образом, эллиптические кривые, допускающие вложение в конечные поля с небольшой степенью k, не могут быть использованы в криптографии. Таковыми, например, являются все суперсингулярные кривые, имеющие степень вложения k ∈ {1, 2, 3, 4, 5, 6}.
Кривая 
называется суперсингулярной, если ее мощность #E = pr + 1 − t, и p|t.
Примером суперсингулярной кривой может служить кривая E: 
(mod p), если характеристика поля p ≡ 2 (mod3), тогда E содержит p + 1 элемент, t = 0 и E имеет степень вложения, равную 2.
Способ вычисления дискретного логарифма на ЭК, использующий сведение Вейля, получил называние MOV-атаки.
Многие протоколы, использующие шифрование и электронные цифровые подписи на эллиптических кривых, специально запрещают использование суперсингулярных кривых. Таким образом, суперсингулярные кривые были изъяты из криптографии.
Однако в 2002 году А.Джоукс нашел неожиданное применение спариванию Вейля и суперсингулярным кривым для построения однораундового протокола выработки общего секретного ключа на основе метода Диффи-Хеллмана. Далее были найдены и другие, не менее интересные приложения такие, как, например, построение открытого ключа пользователя на основе его общеизвестных идентификационных данных таких, как, например, имя или адрес электронной почты (identity based open keys) (см. Advances in Elliptic Curve [?]).
Вычисление кратного точки ЭК с помощью MOV– алгоритма
Пусть заданы эллиптическая кривая EC: y2 = 
(modpr), и точки P, Q ∈ EC порядка n, где n–простое число, причем существует m такое, что Q = mP. Требуется найти множитель m. Отображение Вейля будем обозначать через e(X,Y). Алгоритм вычисления m заключается в
следующем:
1. Находим случайную точку 
2. Находим порядок M точки T.
3. Находим d =Н.О.Д.(n,M). Если d = 1, то возвращаемся к п.1. Иначе, перейдем к следующему пункту. Определим, что в этом случае т.T имеет порядок n.
4. Вычислим a = e(P,T) и с = e(Q,T).
5. Вычисляя дискретный логарифм в поле 
, найдем искомый множитель m.
Отметим, что можно выполнять этот алгоритм с составным n, тогда число d может оказаться собственным делителем n и найденный множитель окажется равным m mod d. В этом случае можно повторять вычисление с различными точками Ti, вычисляя mi = m mod di до тех пор, пока
произведение различных di не станет больше или равно n. После этого можно найти m с помощью китайской теоремы об остатках.
Замечание. Если речь идет о произвольной точке Q, то прежде, чем вычислять дискретный логарифм, полезно знать, найдется ли такое m, что Q = mP. Эту проверку можно выполнить, используя следующее утверждение:
Теорема 6.1. Для произвольной т. 
найдется число m такое, что Q = mP в том и только в том случае, если выполняются два условия:
1. nQ = ∞,
2. e(P, Q) = 1.
19. Пусть Е: - эллиптическая кривая над алгебраически замкнутым полем К, n-положительное число и E[n] – подгруппа точек кривой Е порядка n: 
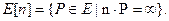(1)
Пусть точка 
Рассмотрим дивизор 
Его степень равна 0, а сумма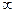 
. По теореме 6.2 найдется функция 
дивизор которой равен D:
(2)
Будем называть функцию удовлетворяющую (2), функцией Вейля.
Алгоритм Миллера вычисления функции Вейля 
1. Найдем бинарное представление числа 
2. Определим исходные значения переменной Z и функции f равными P и 1 соответственно.
3. Выполняем цикл по i от i = t – 1 до i = 0:
Установим 
Если 
тогда выполним операцию сложения P + Z: 
4. Определим выходное значение функции Вейля 
20. Преобразование Вейля. Пусть Е: - эллиптическая кривая над алгебраически замкнутым полем К, n-положительное число и E[n] – подгруппа точек кривой Е порядка n:
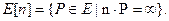(1)
Пусть точка Пусть 
не принадлежит орбите P, т.е не совпадает ни с каким кратным 
точки Т. Рассмотрим дивизоры 
где R – произвольно выбранная точка.
Опр.
Отображение Вейля – это билинейное отображение 
где 
- подгруппа по умножению корней n-й степени из 1 поля К, задаваемое следующей формулой: 
или другой вид 
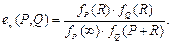
Преобразование Тейта. Пусть точка Обозначим через 
множество точек 
а через 
мн-во классов эквивалентностей кривой Е по множеству .
Опр.
Отображение Тейта – это билинейное отображение 
где - подгруппа по умножению корней n-й степени 1 поля 
задаваемое следующей формулой: 
где 
Важным отличием отображения Тейта от преобразования Вейля является то, что оно не вырождено (не равно 1) при P = Q.
21. Использование преобразования Вейля в трехстороннем протоколе Диффи-Хелмана.
Идея алгоритма Диффи-Хеллмана легко может быть обобщена на несколько участников. Приведем пример для случая n = 3:
1. Каждый из участников A, B, и C вырабатывает секретный ключ
, 
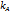и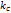 
соответственно и вычисляет точки 
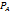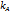= G, 
= G и
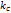= G, которые пересылает по циклу A к B, B к C, C к A.
2. Далее, участники A, B, и C вычисляют точки 
= 
, QB =
, 
= 
соответственно и пересылают по тому же циклу.
3. На последнем шаге вычисляется общая точка R = 
G,
домножением точки, полученной на предыдущем шаге, на соответствующий
секретный ключ: R = G = 
= 
= 
Замечание 1. Выполнение протокола Диффи-Хеллмана для двух
участников требует два обмена данными, для трех – уже шести обменов, а
для произвольного n – n! обменов данными, что является слишком большим
числом при сравнительно небольших n.
Основной ответ:
Протокол Диффи-Хеллмана генерации общего секретного ключа для трех
участников (Tripple Diffi–Hellman) с использованием преобразований Вейля–Тейта.
Рассматривается эллиптическая кривая EC: 
и точка P большого порядка n.
Каждый из участников A,B и C выбирает случайное число 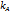, и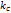
на интервале [2; n − 1] и вычисляет точку 
, 
, 
соответственно, которую пересылает остальным участникам.
3. Теперь каждый участник вычисляет общий элемент конечного расширения поля 
,
где n| 
− 1 по формуле
k = 
= 
= 
= 
Выигрышем применения преобразований Вейля–Тейта является
уменьшение числа информационных обменов по сети (от 6 до 3).
22. Сведение проблемы вычисления кратного на ЭК к проблеме дискретного логарифмирования в конечных полях.
Пусть заданы эллиптическая кривая EC: 
,
и точки P, Q ∈ EC порядка n, где n–простое число, причем существует
m такое, что Q = mP. Требуется найти множитель m. Отображение Вейля
будем обозначать через e(X, Y). Алгоритм вычисления m заключается в
следующем:
1. Находим случайную точку T ∈ EC().
2. Находим порядок M точки T.
3. Находим d =Н.О.Д.(n,M). Если d = 1, то возвращаемся к п.1.
Иначе, перейдем к следующему пункту. Определим, что в этом случае т.T
имеет порядок n.
4. Вычислим a = e(P, T) и с = e(Q, T).
5. Вычисляя дискретный логарифм в поле , найдем искомый
множитель m.
Отметим, что можно выполнять этот алгоритм с составным n, тогда
число d может оказаться собственным делителем n и найденный множитель
окажется равным m mod d. В этом случае можно повторять вычисление
с различными точками Ti, вычисляя mi = m mod di до тех пор, пока
произведение различных di не станет больше или равно n. После этого можно
найти m с помощью китайской теоремы об остатках.
Замечание. Если речь идет о произвольной точке Q, то прежде,
чем вычислять дискретный логарифм, полезно знать, найдется ли такое
m, что Q = mP. Эту проверку можно выполнить, используя следующее
утверждение:
Теорема.
Для произвольной т.Q ∈ EC(Fqk) найдется число m такое,
что Q = mP в том и только в том случае, если выполняются два условия:
1. nQ = ∞,
2. e(P,Q) = 1.
23.Вирусы, их виды и классификация.
1) Компьютерные вирусы – самовоспроизводящаяся программа размещающаяся на жестком диске.
2) Сетевой червь.
3) Троянский конь – вредоносное ПО, внедряющееся или заменяющее полезные программы.
4) Программы зомби – перехватывающие управление компьютером для удаленных хакеров.
5) Шпионские программы.
6) Программы для фишинга (рекламные) – обманные рассылки с целью получения конфиденциальной информации или коммерческой выгода.
7) Pharming – переход на поддельные сайты маскирующиеся под легальные.
8) Мобильные вирусы.
