Пусть n – составное число. Время разложения зависит от размера наименьшего делителя: n=p*q. Если p<<q, то найдено будет достаточно быстро.
Алгоритм хорошо распараллеливается и зависит от гладкости количества точек на выбранной кривой.
Суть алгоритма Ленстры заключается в выборе на псевдокривой EC(Zn) произвольной базовой точки P0 и домножении ее на всевозможные простые числа и их степени пока не получим kP0 = ∞ (mod p) (*), где p–один из делителей n.
#EC – число точек: занимает интервал [p + 1 -2√p, p + 1 + 2√p].
Алгоритм:
Zn – основное множество для координат точек эллиптической кривой EC(Zn): y2= x3 + ax + b, 0 < a,b <p.
Инициализация: //этого в лекциях не было
1. Выберем некоторое значение B1, например, B1 = 10000.
2. Выберем случайным образом числа x, y, a из [0, n − 1].
3. Вычислим b = y2−x3−ax mod n и g = НОД(n, 4a3+27b2). Если
g = n, возвращаемся к п.2. Если 1 < g < n, тогда прекратим вычисление –
делитель найден. Иначе, определим кривую E: y2= x3+ ax + b и базовую
точку-генератор P0(x, y).
4. Присвоим изменяемому параметру P(x, y) начальное значение, равное P0.
Вычисление:
С = p1k1 * p2k2 * … * ptkt – разложение по простым делителям.
r=max piki (i < t) – степень гладкости, причём pr < B1.
Берём произвольную точку P= P0 и вычисляем:
P1= ∏ piti · P, где piti < B1,
в результате чего точка P домножится на pr.
Продолжим вычисление до тех пор, пока не будут пройдены все простые числа, меньшие B1, или не найдется шаг, на котором выполнится условие
НОД(n, P1) = d > 1.
Если выполнится последнее условие, то искомый делитель n найден.
Иначе, либо увеличиваем B1 и повторяем все заново, либо переходим
ко второй стадии алгоритма.
Вторая стадия алгоритма: //и этого тоже
На второй стадии алгоритма предполагается, что число точек #EC
на выбранной ЭК имеет лишь один делитель q, превышающий границу 1-й
стадии B1.
1. Выберем новую границу B2, и выпишем все простые числа из интервала [B1; B2]: {q1, q2,..., qm }.
2. Будем последовательно вычислять точки q1 ·P, q2 ·P, q3 ·P,... пока
не дойдем до границы B2, либо не выполнится условие (*).
Дивизоры
Построение отображения Вейля и родственного ему отображения Тейта основано на теории дивизоров (делителей) алгебраических кривых, разработанной Андре Вейлем.
Идея понятия дивизора основана на том наблюдении, что коэффициенты любого полинома можно вычислить с точностью до ненулевого множителя, зная корни этого многочлена и их кратность.
Действительно, если многочлен P(x) имеет своими корнями кратности ri элементы xi, то 
.
В нашем случае класс изучаемых функций состоит из дробно-рациональных функций над эллиптическими кривыми, т.е. отношений двух многочленов от двух переменных x и y, определенных на точках некоторой эллиптической кривой.
Пусть теперь E: 
–эллиптическая кривая над полем K, а f(x,y): E → K –дробно-рациональная функция. Если f – не константа, то существует не более конечного числа точек P ∈ E, в которых f(P) = 0 или f(P) = ∞. Точки первого вида называются нулями функции f, а второго –
полюсами f. С точностью до ненулевого множителя функцию f можно задать, перечисляя все ее нули и полюсы и задавая их кратность. Если f имеет нуль (полюс) кратности k в точке P, то f можно представить в виде произведения 
, где up имеет в точке P нуль (полюс) первого порядка, а 
Функция up называется униформизатором функции f в точке P.
Определение 6.1. Пусть E: – эллиптическая кривая над полем k. Дивизором D над кривой E называется формальная сумма вида 
,
в которой коэффициенты rP – целые числа и число слагаемых с ненулевым коэффициентом rP
– конечно. Множество точек P, для которых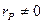 
, называется носителем (support) дивизора D и обозначается supp(D). Целое число 
P ∈ supp(D), называется степенью D и обозначатся deg(D).
Точка эллиптической кривой, равная 
, называется суммой дивизора D и обозначается sum(D).
Сумма дивизоров определяется естественным образом. Множество дивизоров эллиптической кривой образует аддитивную группу относительно операции сложения, а нулем является дивизор, у которого все коэффициенты равны 0. В группе дивизоров наиболее важную роль играют дивизоры функций, которые называются главными дивизорами (principal divisors).
Вычислим дивизор прямой l: ax + by + c, проходящей через две заданные точки P1(x1, y1) и P2(x2, y2) эллиптической кривой E. Если l не является касательной в т.P1 и P2, то она пересекает E и в третьей т.P3(x3, y3), а также в бесконечно удаленной точке ∞. В точках P1, P2 и P3 прямая l имеет нули 1 порядка, а в т. ∞ – полюс 3 порядка. Чтобы увидеть это, перепишем уравнение ЭК в следующем виде:
(1) откуда 
(2).
Из уравнения (1) следует, что x/y обращается в 0 в т.∞, а уравнение (2) показывает, что функция x/y является униформизатором 
в т.∞ и т.∞ является нулем второго порядка для . Значит т.∞ является полюсом 2 порядка для x. Так как y = x · (y/x), то т.∞ является полюсом 3 порядка для y и для функции l = Ax + By + C. Отсюда дивизор прямой l имеет вид 
(3). Проведем через т.P3 вертикальную прямую v = x – x3. Она проходит через т.P3(x3, y3), −P3(x3, −y3) и т.∞, а ее дивизор имеет вид
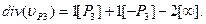. (4)
Из формул (3) и (4) получим 
Так как P1 + P2 = −P3 на кривой E, то последнюю формулу можно переписать в виде 
(5).
Из формул (3) и (4) можно видеть, что согласно определению 6.1 степени прямых lP1,P2 и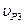 
равны 0, а их сумма равна ∞, что является примером общего факта, выражаемого следующей теоремой:
Теорема 6.2. Дивизор D эллиптической кривой E, имеющий степень 0, является дивизором некоторой функции тогда и только тогда, когда sum(D) = ∞.
Функции от дивизоров
Отображение, задаваемое формулой (7), является групповым гомоморфизмом из аддитивной группы дивизоров в мультипликативную группу поля K, т.к. f(D1 + D2) = f(D1) · f(D2), f(D1 − D2) = f(D1)/f(D2) (6)
Распространяя формулы (6) на произвольные дивизоры, получим формулу 
(7).
Теорема 6.3.(закона взаимности Вейля) Если f и g – функции на эллиптической кривой такие, что
div(f) и div(g) не имеют общих точек, тогда выполняется следующая
формула: f(div(g)) = g(div(f)).
