Алгоритм ECDSA (Elliptic Curve Digest Signature Algorithm) принят в
качестве стандартов ANSI X9F1 и IEEE P1363.
Создание ключей:
1. Выбирается эллиптическая кривая 
(a, b). Число точек на ней должно
делиться на большое простое число n.
2. Выбирается базовая точка G ∈ (a, b) порядка n, n · G = ∞.
3. Выбирается случайное число d ∈ (1, n).
4. Вычисляется Q = d · G.
5. Закрытым ключом является d, открытым ключом - кортеж < a, b, G, n,Q >.
Создание подписи:
1. Выбирается случайное число k ∈ (1, n).
2. Вычисляется k · G = (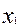
, 
) и r = 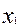(mod n).
3. Проверяется условие r 
0, так как иначе подпись не будет зависеть от закрытого ключа. Если r = 0, то выбирается другое случайное число k.
4. Вычисляется 
(mod n).
5. Вычисляется s = · (Н(M) + d·r) (mod n).
H(M) – хэш-функция от сообщения М.
6. Проверяется условие s 0, так как в этом случае необходимого для
проверки подписи числа 
(mod n) не существует. Если s = 0, то
выбирается другое случайное число k.
Подписью для сообщения М является пара чисел (r, s).
Проверка подписи:
1. Проверим, что числа r и s принадлежат диапазону чисел (1, n).
В противном случае результат проверки отрицательный, и подпись
отвергается.
2. Вычислить w = 
(mod n), и H(M),
3. Вычислить 
= H(M) ·w (mod n), и 
= r·w (mod n)
4. Вычислить · P + · Q = (
, 
), v = (mod n)
Спаривание Вейля-Тейта 112
5. Подпись верна в том и только том случае, когда v = r.
13. Определение. Полем называется кольцо с единицей, в котором каждый ненулевой элемент 
обладает обратным 
. Другими словами, кольцо с единицей является полем, если множество ненулевых элементов образует группу по умножению. Эту группу называют мультипликативной группой поля F и обозначают символом F*.
Пример 1. Полями являются множества рациональных чисел Q, действительных чисел R, комплексных чисел C относительно операций сложения и вычитания.
Пример 2. Кольцо вычетов ZN по модулю числа N является полем, если N – простое число. Число N называется характеристикой поля.
Пусть K – поле, а f(x) – многочлен, неразложимый в K в произведение многочленов меньшей степени. Такой многочлен называется неприводимым над полем K. Свойство неприводимости существенно зависит от свойств поля K, поскольку если в качестве K взять поле комплексных чисел, то любой многочлен является разложимым в произведение линейных многочленов. Подобно кольцу классу вычетов ZN можно рассматривать классы эквивалентности по модулю многочлена f(x).
Пример 3. Кольцо вычетов многочленов по модулю неприводимого многочлена f(x) с коэффициентами из поля K образует поле.
Если K – конечное поле, содержащее p элементов (p – простое число), а f(x) – многочлен степени m, то поле вычетов содержит 
элементов. Такие поля называются полями Галуа в честь выдающегося французского математика Эвариста Галуа, погибшего на дуэли в 20-летнем возрасте, и обозначают символом 
. В курсе алгебры доказывается, что любое конечное поле является полем Галуа для некоторого основания p и степени m. Еще один важный факт, касающийся полей Галуа, состоит в том, что мультипликативная группа конечного поля K всегда является циклической, т.е. существует порождающий элемент x такой, что любой ненулевой элемент y поля K является степенью x 
