Обеспечение доступности информационных ресурсов,
Обеспечение целостности информационных ресурсов и поддерживающей инфраструктуры,
Обеспечение конфиденциальности информационных ресурсов.
Поясним понятия доступности, целостности и конфиденциальности.
Доступность - это возможность за приемлемое время получить требуемую информационную услугу. Доступность информационных сервисов одновременно предполагает ограничение несанкционированногодоступа, защиту сервисов от незаконного вторжения и захвата этих услуг.
Под целостностью подразумевается актуальность и непротиворечивость информации, ее защищенность от разрушения и несанкционированного изменения. Наконец, конфиденциальность - это защита от несанкционированного доступа к информации, чтения ее лицами, не имеющими соответвующих прав.
Информационные системы создаются для получения определенных информационных услуг. Если по тем или иным причинам предоставить эти услуги пользователям становится невозможно, это, очевидно, наносит ущерб всем субъектам информационных отношений. Поэтому, не противопоставляя доступность остальным аспектам, мы выделяем ее как важнейший элемент информационной безопасности.
2. Классификация криптографических методов. Все методы шифрования принято делить на классические и методы шифрования с открытым ключем. Их также принято называть одно- и двух- ключевыми методами, поскольку в классическим шифрах для шифрования/расшифрования используется один и тот же ключ, в то время как в современных методах шифрования с открытым ключем используется два ключа – public key (публичный открытый ключ) и private key (личный закрытый ключ). Использование двух ключей позволяет преодолеть главный недостаток классических шифров – проблему распределения ключей. Методы, использующие один ключ, называются также симметричными, а использующие два ключа – асимметричными.
В свою очередь классические (одноключевые) методы шифрования делятся на две основные группы – потоковые и блочные. Потоковые методы шифруют входной поток данных посимвольно (или побитово). Шифрование каждого символа (бита) текста производится независимо от результата шифрования соседних символов (битов). Потоковые методы являются наиболее быстрыми, дешевыми и достаточно надежными методами шифрования.
Типичным представителем потокового метода шифрования является метод RC4 с переменной длиной ключа, разработанный в 1987 году Роном Ривестом из корпорации RSA Data Security, Inc. Этот метод широко используется в разных приложениях, например, в протоколе WEP для шифрования данных, передаваемым по беспроводным сетям Wi-Fi между точкой доступом (Access Point) и беспроводным адаптером на компьютере клиента. Ключом в методе RC4 является любая символьная последовательность длины до 256 байт, например, условная фраза или произвольный набор чисел. До 1994 года алгоритм RC4 держался в секрете и распространялся среди производителей под подписку о неразглашении, однако в 1994 году анонимный хакер опубликовал алгоритм метода в сети Usenet, после чего метод перестал был секретным. Однако это не ослабило его стойкость по отношению к атакам, и по настоящее время не найдено методов взлома RC4, которые были бы значительно лучше, чем полный перебор.
Этот метод имел ограничения по экспорту для использования с ключом более 40 байт, однако, нет никаких оснований предполагать, что ключ длины 40 байт является ненадежным, поскольку 40 байт=320 бит, а полный перебор 320-битового ключа лежит далеко за пределами сегодняшних возможностей и маловероятно, что когда-нибудь окажется возможным. Ниже мы опишем схему метода RC4.
Метод RC4. Инициализация.
1. Определяются два массива К и S длины 256 типа Byte.
2. Выбирается ключ Key, представляющий набор символов длины не более 256 байт.
3. Заполняем массив К кодами символом из ключа Key. Если длина ключа Key меньше 256, то используем ключ несколько раз (заполняя массив K полностью).
4. Инициализация S-блока. Сначала заполним его линейно:
S(0)=0, S(1)=1, …, S(255)=255
5. В цикле выполняем перестановку S-блока:
for i = 0 to 255:
j=(j + S(i) + K(i)) mod 256 //поменять местами S(i) и S(j)
temp=S(i): S(i)=S(j): S(j)=temp
Next i
Шифрование. Организуем цикл, в котором считываем посимвольно текст, который надо закодировать, и одновременно генерируем ключевую последовательность, которая используется для сдвига символов текста:
‘ инициализируем начальные значения i, j произвольными значения от 0 до 255
i=i0: j=j0 Do while not eof(1)
i = (i +1) mod 256 j
j=(j + Si) mod 256
‘меняем местами S(i) и S(j)
temp=S(i): S(i)=S(j): S(j)=temp
t = (S(i) + S(j) mod 256 k=S(t)
‘ Считываем очередной символ из текста
m = Input(1, #1)
‘к ASCII-коду полученного символа m добавляет по модулю 256 элемент ключевой
‘последовательности k=S(t)
enc=(Asc(m)+k) mod 256
‘записываем в выходной поток закодированный символ
write #2, enc
End Do
4. Тест Миллера Рабина. Пусть R – произвольное натуральное число.
1.Выполняем разложение R–1 = 2s∙t, где t – нечетное число.
2.Выбираем случайное число a, 1 < a < R-1. Проверим, что R не делится на а нацело. Если делится, то R – составное. Иначе, продолжим тест.
3.Вычисляем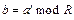 
. Если b равно 1, то R – вероятно простое число. Продолжаем тест со следующим a. Иначе, перейдем к следующему пункту.
4.Последовательно выполняем итерацию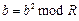 
до тех пор, пока b не станет равным R–1, либо число итераций не превысит s-1, где s взято из пункта 1.
Если раньше выполнится b = R–1, то число R – вероятно простое, иначе R – составное.
5.Повторим процедуру с новым а.
После k циклов вероятность того, что R – составное, меньше 4-k, т.е. убывает очень быстро.
5. Метод RSA. Он основан на вычислительной сложности задачи разложения очень больших целых чисел на простые сомножители.
Генерация параметров метода.
1.Выбираем два больших простых числа p и q.
2.Вычисляем N = p∙q, и функцию Эйлера 
(значение 
равно количеству натуральных чисел k < N, взаимно простых с N).
3.Находим число e, взаимно-простое с 
,
4.Находим число d из условия наибольший общий делитель e ∙ d = 1 mod . Для нахождения d используем расширенный алгоритм Евклида. Для этого решим в целых числах уравнение 
. (*)
5.Значение d положим равным найденному b. Если множитель b окажется меньшим нуля, следует заменить его на 
.
Пара (N,e) объявляется открытым ключом и используется для шифрования. Параметр d является секретным и используется для расшифровки данных.
Шифрование производится по формуле 
, где x – код исходного символа. Раскодирование производится по формуле 
, и основано на теореме Эйлера 
. Проверим вычисление. Из формулы (*)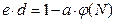 
получим 
6. Алгоритм шифрования ЭльГамаля. Он базируется на трудности вычисления дискретного логарифма. Для генерации пары ключей сначала берется большое простое число p и два случайных числа g и x, каждое из которых меньше p. Затем вычисляется 
. Общедоступными ключами являются y, g и p, а секретным ключом является х. Для шифрования сообщения M выполняем следующее:
1.Выбираем случ. число k, чтобы НОД(k, p-1)=1.
2.Вычисляем 
,
3.Вычисляем 
. Пара (a, b) является шифротекстом.
Для расшифровки шифротекста, вычисляем 
.
Сделаем проверку: 
Пример. Выберем p=11, g=2, секретный ключ x=8. Вычисляем 
Пусть cообщение M=5. Выбираем случайное число K=9. Убедимся, что НОД(k, p-1)=НОД(9, 10)=1. Вычисляем пару (a, b):
, 
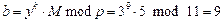, (a, b)=(6, 9)-шифрограмма.
Для расшифровки сообщения (a, b), находим
, откуда, 
. Поскольку, 
, то 
, откуда M=5.
7. Метод выработки секретного ключа Диффи-Хелмана. Выработка общего секретного ключа двумя пользователями, находящимя в условиях, когда все пересылаемые ими данные, доступны третьему лицу.
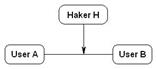
Сначала генерируются два больших простых числа n и q. Эти два числа не являются секретными. Далее один из партнеров A генерирует случайное число x<n и посылает другому участнику будущих обменов B значение M = qx mod n
Партнер B генерирует случайное число у<n и посылает A вычисленное значение K = qy mod n. Партнер A, получив K, вычисляет Cx = Kx mod n, а партнер В вычисляет Cy = My mod n. Алгоритм гарантирует, что числа Cy и Cx равны и могут быть использованы в качестве секретного ключа для шифрования.
Алгоритм Диффи-Хелмана, обеспечивая конфиденциальность передачи ключа, не может гарантировать того, что он прислан именно тем партнером, который предполагается. Для решения этой проблемы можно использовать технику электронной подписи. Например, сообщения M и K, которыми обмениваются пользователи, подписываются их цифровыми подписями, что исключает подлог.
8.Электронно-цифровая подпись. Её свойства и правовые основы. Алгоритм создания ЭЦП.
Одной из наиболее важных задач информационной безопасности является сохранение целостности (неизменности) электронных документов, передаваемых через каналы связи. Таким средством является электронно-цифровая подпись (ЭЦП), которая сохранила основные свойства обычной подписи:
- подпись аутентична, то есть с ее помощью получателю документа можно доказать, что она принадлежит подписывающему;
- подпись неподделываема; то есть служит доказательством, что только тот человек, чей автограф стоит на документе, мог подписать данный документ, и никто иной.
- Подпись непереносима, то есть является частью документа и поэтому перенести ее на другой документ невозможно.
- Документ с подписью является неизменяемым.
- Подпись неоспорима.
- Любое лицо, владеющее образцом подписи может удостоверится, что документ подписан владельцем подписи.
Существует несколько методов построения ЭЦП, а именно:
- шифрование электронного документа (ЭД) на основе симметричных алгоритмов. Данная схема предусматривает наличие в системе третьего лица–арбитра, пользующегося доверием обеих сторон. Авторизацией документа в данной схеме является сам факт зашифрования ЭД секретным ключом и передача его арбитру.
- Использование ассиметричных алгоритмов шифрования. Фактом подписания документа является зашифрование его на секретном ключе отправителя.
- Развитием предыдущей идеи стала наиболее распространенная схема ЭЦП – зашифрование окончательного результата обработки ЭД хеш-функцией при помощи асимметричного алгоритма.
Кроме перечисленных, существуют и другие методы построения схем ЭЦП - групповая подпись, неоспариваемая подпись, доверенная подпись и др. Появление этих разновидностей обусловлено разнообразием задач, решаемых с помощью электронных технологий передачи и обработки электронных документов.
ЭЦП - это программно-криптографическое средство, которое обеспечивает решение следующих задач:
1. проверку целостности документов;
2. конфиденциальность документов;
3. идентификация лица, отправившего документ;
Правовые основы электронно-цифровой подписи регламентируются несколькими законами Российской Федерации. В частности, пункт 3 статьи 5 Федерального закона "Об информации, информатизации и защите информации" гласит: "Юридическая сила документа, хранимого, обрабатываемого и передаваемого с помощью автоматизированных информа-ционных и телекоммуникационных систем, может подтверждаться электронной цифровой подписью.10 января 2002 года Президентом РФ был подписан очень важный закон "Об электронной цифровой подписи" номер 1-ФЗ (принят Государственной Думой 13 декабря 2001 года), развивающий и конкретизирующий основные положения закона "Об информации, информатизации и защите информации". Его роль поясняется в статье 1.
1. Целью настоящего Федерального закона является обеспечение правовых условий использования электронной цифровой подписи в электронных документах, при соблюдении которых электронная цифровая подпись в электронном документе признается равнозначной собственноручной подписи в документе на бумажном носителе.
2. Действие настоящего Федерального закона распространяется на отношения, возникающие при совершении гражданско-правовых сделок и в других предусмотренных законодательством Российской Федерации случаях. Действие настоящего Федерального закона не распространяется на отношения, возникающие при использовании иных аналогов собственноручной подписи.
Закон вводит следующие основные понятия:
Электронный документ - документ, в котором информация представлена в электронно-цифровой форме.
Электронная цифровая подпись - реквизит электронного документа, предназначенный для защиты данного электронного документа от подделки, полученный в результате криптографического преобразования информации с использованием закрытого ключа электронной цифровой подписи и позволяющий идентифицировать владельца сертификата ключа подписи, а также установить отсутствие искажения информации в электронном документе.
Владелец сертификата ключа подписи - физическое лицо, на имя которого удостоверяющим центром выдан сертификат ключа подписи и которое владеет соответствующим закрытым ключом электронной цифровой подписи, позволяющим с помощью средств электронной цифровой подписи создавать свою электронную цифровую подпись в электронных документах (подписывать электронные документы).
Средства электронной цифровой подписи - аппаратные и (или) программные средства, обеспечивающие реализацию хотя бы одной из следующих функций: создание электронной цифровой подписи в электронном документе с использованием закрытого ключа электронной цифровой подписи, подтверждение с использованием открытого ключа электронной цифровой подписи подлинности электронной цифровой подписи в электронном документе, создание закрытых и открытых ключей электронных цифровых подписей.
Сертификат средств электронной цифровой подписи - документ на бумажном носителе, выданный в соответствии с правилами системы сертификации для подтверждения соответствия средств электронной цифровой подписи установленным требованиям.
Закрытый ключ электронной цифровой подписи - уникальная последовательность символов, известная владельцу сертификата ключа подписи и предназначенная для создания в электронных документах электронной цифровой подписи с использованием средств электронной цифровой подписи.
Открытый ключ электронной цифровой подписи - уникальная последовательность символов, соответствующая закрытому ключу электронной цифровой подписи, доступная любому пользователю информационной системы и предназначенная для подтверждения с использованием средств электронной цифровой подписи подлинности электронной цифровой подписи в электронном документе.
Сертификат ключа подписи - документ на бумажном носителе или электронный документ с электронной цифровой подписью уполномоченного лица удостоверяющего центра, которые включают в себя открытый ключ электронной цифровой подписи и выдаются удостоверяющим центром участнику информационной системы для подтверждения подлинности электронной цифровой подписи и идентификации владельца сертификата ключа подписи.
Подтверждение подлинности электронной цифровой подписи в электронном документе - положительный результат проверки соответствующим сертифицированным средством электронной цифровой подписи с использованием сертификата ключа подписи принадлежности электронной цифровой подписи в электронном документе владельцу сертификата ключа подписи и отсутствия искажений в подписанном данной электронной цифровой подписью электронном документе.
Пользователь сертификата ключа подписи - физическое лицо, использующее полученные в удостоверяющем центре сведения о сертификате ключа подписи для проверки принадлежности электронной цифровой подписи владельцу сертификата ключа подписи.
Информационная система общего пользования - информационная система, которая открыта для использования всеми физическими и юридическими лицами и в услугах которой этим лицам не может быть отказано.
Корпоративная информационная система - информационная система, участниками которой может быть ограниченный круг лиц, определенный ее владельцем или соглашением участников этой информационной системы.
Юридическая сила электронной цифровой подписи признается при наличии в автоматизированной информационной системе программно-технических средств, обеспечивающих идентификацию подписи, и соблюдении установленного режима их использования". Такая формулировка предполагает, что электронный документ может быть заверен ЭЦП и использован в тех случаях, когда явно не предусмотрены другие требования к форме документа, т.е. введение данной нормы, по существу, не расширило возможности использования ЭДО в гражданском обороте.Развитие основных типов криптографических протоколов (ключевой обмен, электронно-цифровая подпись (ЭЦП), аутентификация и др.) было бы невозможно без создания открытых ключей и построенных на их основе асимметричных протоколов шифрования. Эти методы рассматриваются в следующем разделе.
