Выражение для вольтамперной характеристики (ВАХ) идеализированного перехода приведено в [1,2]
[ exp ( 
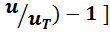,(2.5) где 
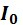– обратный тепловой ток, называемый также током насыщения перехода, 
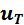– термический потенциал.
В симметричном переходе (ND 
NА) необходимо учитывать обе составляющие обратного тока, создаваемые неосновными носителями заряда (и электронами и дырками). В этом случае выражение для теплового тока имеет вид
+ 
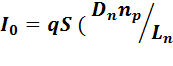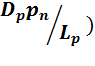, (2.6)
где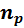 
и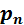 
– концентрации неосновных электронов и дырок, 
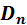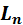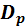и 
, 
и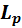 
– коэффициенты диффузии и диффузионные длины электронов и дырок соответственно, 
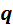– заряд электрона, 
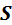– площадь поперечногосеченияперехода. В несимметричном переходе при ND 
NА дырочную составляющую можно не учитывать. В этом случае
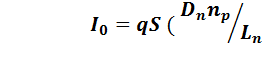). (2.7)
Тепловой ток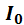 
получил свое название в связи с тем, что неосновные носители появляются в примесном полупроводнике за счет тепловой генерации, и их концентрация и, соответственно, величина этого тока экспоненциально увеличиваются с ростом температуры. Термин ток насыщения подчеркивает тот факт, что этот ток не зависит от приложенного к переходу напряжения.
Для построения приведенного на рис. 2.4. графика ВАХ идеализированного перехода удобно раскрыть скобки в выражении (2.5):
exp (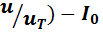 
.(2.8)
Здесь первое слагаемое отражает ток, создаваемый основными носителями заряда, и он экспоненциально зависит от напряжения. Второе слага-емое представляет собой ток, создаваемый неосновными носителями, и он от напряжения не зависит. На рис. 2.4. указанные составляющие тока приведены штриховыми линиями, а сплошной линией показана их сумма, т.е. ВАХ идеализированного перехода. Следует отметить, что поскольку мас-штаб по оси токов одинаков на прямой и обратной ветви, на графике представлен только самый начальный участок прямой ветви, на котором пря-
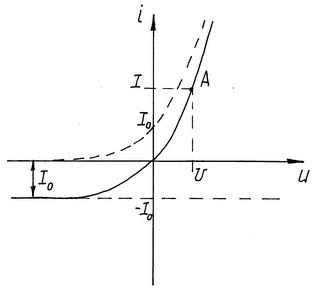
Рис. 2.4. Вольтамперная характеристика
идеализированного перехода.
мой ток соизмерим с обратным тепловым током. Такой режим часто называют режимом микротоков.
Как видно из рисунка, ВАХ идеализированного перехода нелинейна. Для нелинейных элементов особый интерес представляет вопрос об их электрическом сопротивлении. Во-первых, сопротивление нелинейного двухполюсника постоянному току, называемое также статическим сопротивлением, не является постоянным, а зависит от того, в к акой конкретной точке на ВАХ оно определяется (эта точка обычно называется рабочей точкой). Для иллюстрации сказанного на рис. 2.4 на прямой ветви указана точка А и показаны величины напряжения U и тока I, соответствующие этой точке. В этом случае сопротивление перехода постоянному току в соответствии с законом Ома будет равно
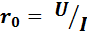. (2.9)
Если рабочая точка будет смещаться по ВАХ вверх от точки А, то в силу нелинейности ВАХ напряжение при этом будет увеличиваться все меньше, а ток, напротив, будет увеличиваться все сильнее. Нетрудно увидеть, что при этом сопротивление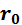 
будет уменьшаться.
Во-вторых, для описания работы нелинейных двухполюсников на переменном токе вводится параметр, называемый дифференциальным сопротивлением
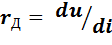. (2.10)
Выражение для дифференциального сопротивления идеализированного перехода получается дифференцированием выражения (2.5)
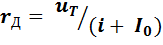. (2.11)
Графически величина дифференциального сопротивления определяется как правило через малые приращения напряжения Δ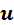 
и тока Δ 
, которые выбираются в окрестности рабочей точки
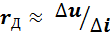. (2.12)
При этом необходимо, чтобы участок ВАХ, соответствующий выбранным приращениям, можно было считать линейным (с удовлетворительной точностью). Это условие получило название критерия так называемого малосигнального приближения, широко используемого в радиотехнике (подробнее см. ниже, в п. 2.7). При подаче на нелинейный двухполюсник малого переменного напряжения дифференциальное сопротивление связывает его амплитуду с амплитудой переменного тока, протекающего через двухполюсник
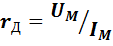. (2.13)
Нетрудно убедиться, что сопротивление постоянному току и дифференциальное сопротивление перехода различаются по величине. На прямой ветви дифференциальное сопротивление меньше сопротивления постоянному току. Важно также отметить, что строго вертикальному участку ВАХ (если такой возможен) соответствует дифференциальное сопротивление равное нулю, а горизонтальному, соответственно, равное бесконечности. Таким образом, как видно из рис. 2.4, дифференциальное сопротивление идеализированного перехода на обратной ветви равно бесконечности.
