Название EGSA происходит от слов El Gamal Signature Algorithm (алгоритм цифровой подписи Эль Гамаля). Идея EGSA основана на том, что для обоснования практической невозможности фальсификации цифровой подписи может быть использована более сложная вычислительная задача, чем разложение на множители большого целого числа – задача дискретного логарифмирования. Кроме того, Эль Гамалю удалось избежать явной слабости алгоритма цифровой подписи RSA, связанной с возможностью подделки цифровой подписи под некоторыми сообщениями без определения секретного ключа.
В алгоритме цифровой подписи Эль Гамаля для того чтобы генерировать пару ключей (открытый ключ – секретный ключ), сначала выбирают некоторое большое простое целое число Р и большое целое число G, причем
G < Р. Отправитель и получатель подписанного документа используют при вычислениях одинаковые большие целые числа Р (~10308 или ~21024) и
G (~10154 или ~2512), которые не являются секретными.
Отправитель выбирает случайное целое число X, 1< X £ (Р – 1), и вычисляет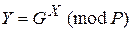 
. Число Y является открытым ключом, используемым для проверки подписи отправителя и открыто передается всем потенциальным получателям документов. Число X является секретным ключом отправителя для подписывания документов и должно храниться в секрете.
Для того чтобы подписать сообщение М, сначала отправитель хэширует его с помощью хэш-функции h () в целое число m = h (M), 1< m <(P – 1), и генерирует случайное целое число K, 1< K < (Р – 1), такое, что K и (Р – 1) являются взаимно простыми. Затем отправитель вычисляет целое число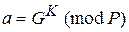 
и, применяя расширенный алгоритм Евклида, вычисляет с помощью секретного ключа X целое число b из уравнения 
.
Пара чисел (а, b) образует цифровую подпись S = (a, b), проставляемую под документом М. Далее тройка чисел (М, а, b) передается получателю, в то время как пара чисел (Х, K) держится в секрете.
После приема подписанного сообщения (М, а, b) получатель должен проверить, соответствует ли подпись S = (a, b) сообщению М.
Для этого получатель сначала вычисляет по принятому сообщению М число m = h (M), т.е. хэширует принятое сообщение М. Затем вычисляет значение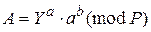 
и признает сообщение М подлинным, если, и только если 
.
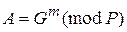Можно строго математически доказать, что равенство
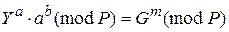
будет выполняться тогда, и только тогда, когда подпись S =(a, b) под документом М получена с помощью именно того секретного ключа X, из которого был получен открытый ключ Y. Таким образом, можно надежно удостовериться, что отправителем сообщения М был обладатель именно данного секретного ключа X, не раскрывая при этом сам ключ, и что отправитель подписал именно этот конкретный документ М.
Следует отметить, что выполнение каждой подписи по методу Эль Гамаля требует нового значения K, причем это значение должно выбираться случайным образом. Если злоумышленник раскроет когда-либо значение K, повторно используемое отправителем, то он сможет раскрыть секретный ключ X.
Схема цифровой подписи Эль Гамаля имеет ряд преимуществ по сравнению со схемой цифровой подписи RSA:
1. При заданном уровне стойкости алгоритма цифровой подписи целые числа, участвующие в вычислениях, имеют запись на 25% короче, что уменьшает сложность вычислений почти в два раза и позволяет заметно сократить объем используемой памяти.
2. При выборе модуля Р достаточно проверить, что это число является простым и что у числа (Р – 1) имеется большой простой множитель (т.е. всего два достаточно просто проверяемых условия).
3. Процедура формирования подписи по схеме Эль Гамаля не позволяет вычислять цифровые подписи под новыми сообщениями без знания секретного ключа (как в RSA).
Однако алгоритм цифровой подписи Эль Гамаля имеет и некоторые недостатки по сравнению со схемой подписи RSA. В частности, длина цифровой подписи получается в 1,5 раза больше, что, в свою очередь, увеличивает время ее вычисления.
