Алгоритм цифровой подписи DSA (Digital Signature Algorithm) предложен в 1991 г. в США для использования в стандарте цифровой подписи DSS (Digital Signature Standard). Алгоритм DSA является развитием алгоритма цифровой подписи Эль Гамаля.
Отправитель и получатель электронного документа используют при вычислении большие целые числа: G и Р – простые числа, L бит каждое (512 < L < 1024); q – простое число длиной 160 бит (делитель числа (Р – 1)). Числа G, P, q являются открытыми и могут быть общими для всех пользователей сети.
Отправитель выбирает случайное целое число X, 1< Х < q. Число X является секретным ключом отправителя для формирования электронной цифровой подписи.
Затем отправитель вычисляет значение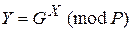 
. Число Y является открытым ключом для проверки подписи отправителя. Число Y передается всем получателям документов.
Этот алгоритм также предусматривает использование односторонней функции хэширования h(). В стандарте DSS определен алгоритм безопасного хэширования SHA.
Для того чтобы подписать документ М, отправитель хэширует его в целое хэш-значение m = h (M), 1 < m < q, затем генерирует случайное целое число K, 1< K < q, и вычисляет число r = (GK (mod P))(mod q). Затем отправитель вычисляет с помощью секретного ключа X целое число 
. Пара чисел r и s образует цифровую подпись S = (r, s) под документом М.
Таким образом, подписанное сообщение представляет собой тройку чисел (М, r, s).
Получатель подписанного сообщения (М, r, s) проверяет выполнение условий 0 < r < q, 0 < s < q и отвергает подпись, если хотя бы одно из этих условий не выполнено.
Затем получатель вычисляет значение
,
хэш-значение m = h (M) и числа u 1 = m × w (mod q), u 2 = m × r (mod q).
Далее получатель с помощью открытого ключа Y вычисляет значение
и проверяет выполнение условия v = r.
Если условие v = r выполняется, тогда подпись S = (r, s) под документом М признается получателем подлинной.
По сравнению с алгоритмом цифровой подписи Эль Гамаля алгоритм DSA имеет следующие основные преимущества:
1. При любом допустимом уровне стойкости, т.е. при любой паре чисел G и Р (от 512 до 1024 бит), числа q, X, r, s имеют длину по 160 бит, сокращая длину подписи до 320 бит.
2. Большинство операций с числами K, r, s, X при вычислении подписи производится по модулю числа q длиной 160 бит, что сокращает время вычисления подписи.
3. При проверке подписи большинство операций с числами u 1, u 2, v, w также производится по модулю числа q длиной 160 бит, что сокращает объем памяти и время вычисления.
Недостатком алгоритма DSA является то, что при подписывании и при проверке подписи приходится выполнять сложные операции деления по модулю q:
, ,
что не позволяет получать максимальное быстродействие.
Следует отметить, что реальное исполнение алгоритма DSA может быть ускорено с помощью выполнения предварительных вычислений. Заметим, что значение r не зависит от сообщения М и его хэш-значения m. Можно заранее создать строку случайных значений K и затем для каждого из этих значений вычислить значения r. Можно также заранее вычислить обратные значения K –1 для каждого из значений K. Затем, при поступлении сообщения М, можно вычислить значение s для данных значений r и K –1. Эти предварительные вычисления значительно ускоряют работу алгоритма DSA.
4.3.4. Алгоритмы электронной цифровой подписи
ГОСТ Р 34.10–94 и ГОСТ Р 34.10–2001
Алгоритм цифровой подписи, определяемый этим стандартом ГОСТ Р 34.10–94, концептуально близок к алгоритму DSA. В нем используются следующие параметры: р – большое простое число длиной от 509 до 512 бит либо от 1020 до 1024 бит; q – простой сомножитель числа (р – 1), имеющий длину 254...256 бит; а – любое число, меньшее (р – 1), причем такое, что
aq (mod p) = 1; х – некоторое число, меньшее q; у = ах (mod p).
Кроме того, этот алгоритм использует однонаправленную хэш-функцию h (х), определенную стандартом ГОСТ Р 34.11–94.
Первые три параметра р, q и а являются открытыми и могут быть общими для всех пользователей сети. Число х является секретным ключом, а число у является открытым ключом.
Чтобы подписать некоторое сообщение M, а затем проверить подпись, выполняются следующие шаги.
1. Отправитель генерирует случайное число k, причем k < q.
2. Отправитель вычисляет значения m = h (M), r = (ak (mod p))(mod q)
s = (x × r + k × m)(mod q). Если m (mod q) = 0, то значение m принимают равным единице. Если r = 0, то выбирают другое значение k и начинают снова. Цифровая подпись представляет собой два числа: r mod 2256 и s mod 2256. Подписанное сообщение отправляется получателю.
3. Получатель проверяет подпись, вычисляя:
v = h (M) q –2 (mod q),
z 1 = s × v (mod q),
z 2 = ((q – r) × v) (mod q),
.
Если u = r, то подпись считается верной.
В 2002 г. в России введен новый стандарт электронной цифровой подписи ГОСТ Р 34.10–2001. Установленная в этом стандарте схема цифровой подписи должна быть реализована с использованием операций группы точек эллиптической кривой. Криптографическая стойкость данной схемы основывается на сложности решения задачи дискретного логарифмирования на эллиптической кривой.
Параметрами схемы цифровой подписи являются.
1. Простое число p – модуль эллиптической кривой, удовлетворяющее неравенству p > 2255.
2. Эллиптическая кривая Ep (a, b), задаваемая своим инвариантом J или коэффициентами a и b.
Инвариантом эллиптической кривой называется величина:
Коэффициенты эллиптической кривой, по известному инварианту, определяются следующим образом
, 
, где 
.
3. Целое число m, удовлетворяющее условию
.
4. Простое число q, для которого выполнены следующие условия:
m = n × q, n ³ 1;
2254 < q < 2256.
5. Точка P ¹ O эллиптической кривой Ep (a, b), с координатами (xP, yP), удовлетворяющая равенству q × P = O.
6. Хэш-функция h, определенная в ГОСТ Р 34.11–94.
Каждый пользователь схемы цифровой подписи должен обладать личными ключами: ключом подписи (целым числом d, удовлетворяющим неравенству 0 < d < q) и ключом проверки (точкой эллиптической кривой Q с координатами (xQ, yQ), удовлетворяющей равенству Q = d × P).
На приведенные выше параметры схемы цифровой подписи накладываются следующие требования:
· должно быть выполнено условие pt ¹ 1(mod q), для всех целых t = 1, 2,... B, где B удовлетворяет неравенству B ³ 31;
· должно быть выполнено неравенство m ¹ p;
· инвариант кривой должен удовлетворять условию 
или 1728.
Исходными данными процесса получения электронной цифровой подписи являются ключ подписи d и подписываемое сообщение M, а выходным результатом – ЭЦП S. Данный процесс заключается в следующем.
1. Вычислить хэш-код сообщения: hM = h (M).
2. Вычислить целое число a, двоичным представлением которого является вектор hM, и определить значение e º a (mod q). Если e = 0, то определить e = 1.
3. Cгенерировать случайное (псевдослучайное) целое число k, удовлетворяющее неравенству 0 < k < q.
4. Вычислить точку эллиптической кривой C = k × P и определить r º xC (mod q), где xC – x-координата точки C. Если r = 0, то повторить предыдущее действие.
5. Вычислить значение s º (r × d + k × e)(mod q). Если s = 0, то подобрать другое число k и повторить шаги 4 и 5.
6. Вычислить двоичные векторы 
и 
, соответствующие r и s, и определить цифровую подпись 
как конкатенацию двух двоичных векторов.
Исходными данными процесса проверки электронной цифровой подписи являются подписанное сообщение M, цифровая подпись S и ключ проверки Q, а выходным результатом – свидетельство о достоверности или ошибочности данной подписи. Для этого необходимо выполнить следующие действия.
1. По полученной подписи S, вычислить целые числа r и s. Если выполнены неравенства 0 < r < q и 0< s < q, то перейти к следующему шагу. В противном случае подпись неверна.
2. Вычислить хэш-код полученного сообщения M: hM = h (M).
3. Вычислить целое число a, двоичным представлением которого является вектор hM, и определить значение e º a (mod q). Если e = 0, то определить e = 1.
4. Вычислить значение v º e –1 (mod q).
5. Вычислить значения z 1 º s × v (mod q) и z 2 º – r × v (mod q).
6. Вычислить точку эллиптической кривой C = z 1× P + z 2× Q и определить R º xC (mod q), где xC – x-координата точки C.
7. Если выполнено равенство R = r, то подпись принимается, в противном случае, подпись неверна.
Вопросы для повторения
1. Опишите алгоритм шифрования с открытым ключом RSA.
2. Опишите алгоритм шифрования с открытым ключом Эль Гамаля.
3. Опишите алгоритм открытого распределения ключей Диффи-Хеллмана.
4. Опишите принципы построения асимметричных криптосистем на основе эллиптических кривых.
5. Опишите алгоритм безопасного хэширования SHA.
6. Опишите алгоритм хэширования ГОСТ Р 34.11–94.
7. Опишите схему ЭЦП на основе алгоритма RSA.
8. Опишите алгоритм ЭЦП Эль Гамаля (EGSA).
9. Опишите алгоритм ЭЦП DSA.
10. Опишите алгоритм ЭЦП ГОСТ Р 34.10–94.
11. Опишите алгоритм ЭЦП ГОСТ Р 34.10–2001.
Резюме по теме
В первой части темы описаны алгоритмы шифрования с открытым ключом: криптосистема RSA, криптосистема Эль Гамаля, криптосистема на основе эллиптических кривых и алгоритм открытого распространения ключей Диффи-Хеллмана. Вторая часть посвящена алгоритмам криптографического хэширования. В ней рассмотрены алгоритм безопасного хэширования SHA (Secure Hash Algorithm), односторонние хэш-функции на основе симметричных блочных алгоритмов, алгоритм хэширования ГОСТ Р 34.11–94. Третья часть содержит описания схем электронных цифровых подписей на основе алгоритма RSA, алгоритма цифровой подписи Эль Гамаля, алгоритма цифровой подписи DSA (Digital Signature Algorithm), алгоритмов ГОСТ Р 34.10–94 и ГОСТ Р 34.10–2001.
