Криптосистемы Диффи-Хеллмана и Эль Гамаля основаны на вычислительной сложности задачи дискретного логарифмирования.
Криптосистема Диффи-Хеллмана была первым алгоритмом с открытыми ключами (предложен в 1976 г.). Вообще говоря, она не является шифром и предназначена для генерации ключа симметричного шифрования, который затем будет использован субъектами информационных отношений для защищенного обмена сообщениями по открытой сети. Эту криптосистему называют алгоритмом открытого распределения ключей Диффи-Хеллмана.
Предположим, что два пользователя А и В хотят организовать защищенный коммуникационный канал.
1. Обе стороны заранее уславливаются о модуле N (N должен быть простым числом) и примитивном элементе g в 
,
(1 < g < N – 1), который образует все ненулевые элементы множества 
, т.е. 
. Установлено, что для любого простого N существует ровно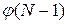 
примитивных элементов. Здесь 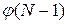– функция Эйлера.
Эти два целых числа N и g могут не храниться в секрете. Как правило, эти значения являются общими для всех пользователей системы. Для обеспечения стойкости число N должно иметь длину, большую или равную 512 бит, и разложение числа N – 1 на множители должно содержать хотя бы один большой простой множитель. При таком выборе числа N в настоящее время не существует эффективного алгоритма для решения задачи дискретного логарифмирования.
2. Затем пользователи А и В независимо друг от друга выбирают собственные секретные ключи 
и 
( и – случайные большие целые числа, которые хранятся пользователями А и В в секрете).
3. Далее пользователь А вычисляет открытый ключ 
, а пользователь В – открытый ключ 
.
4. Затем стороны А и В обмениваются вычисленными значениями открытых ключей 
и 
по незащищенному каналу.
5. Далее пользователи А и В вычисляют общий секретный ключ, используя следующие сравнения:
· пользователь А: 
;
· пользователь В: 
.
При этом K = K', так как 
.
Ключ K может использоваться в качестве общего секретного ключа (ключа шифрования ключей) в симметричной криптосистеме.
Кроме того, обе стороны А и В могут шифровать сообщения, используя следующее преобразование шифрования (типа RSA):
.
Для выполнения расшифрования получатель сначала находит ключ расшифрования 
с помощью сравнения 
, а затем восстанавливает сообщение
.
Рассмотрим пример. Допустим, модуль N = 47, а примитивный элемент g = 23. Предположим, что пользователи А и В выбрали свои секретные ключ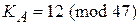и: 
и 
.
Для того чтобы иметь общий секретный ключ K, они вычисляют сначала значения частных открытых ключей:
,
.
После того, как пользователи А и В обменяются своими значениями и , они вычисляют общий секретный ключ:
.
Кроме того, они находят секретный ключ расшифрования, используя следующее сравнение: , откуда 
Теперь, если открытый текст М = 16, то шифртекст 
.
В результате расшифрования получится 
.
Криптосистема Эль Гамаля, предложенная в 1985 г., может быть использована как для шифрования, так и для цифровых подписей. Безопасность схемы Эль Гамаля обусловлена сложностью вычисления дискретных логарифмов в конечном поле.
Для того чтобы генерировать пару ключей (открытый ключ – секретный ключ), сначала выбирают некоторое большое простое число Р и большое целое число G, причем G < Р. Числа Р и G могут быть распространены среди группы пользователей.
Затем выбирают случайное целое число X, причем Х < Р. Число X является секретным ключом и должно храниться в секрете.
Далее вычисляют 
. Число Y является открытым ключом.
Для того чтобы зашифровать сообщение М, выбирают случайное целое число K, 1< K < Р – 1, такое, что числа K и (Р – 1) являются взаимно простыми.
Затем вычисляют числа
;
.
Пара чисел (а, b) является шифртекстом. Заметим, что длина шифртекста вдвое больше длины исходного открытого текста М.
Для того чтобы расшифровать шифртекст (а, b), вычисляют
.
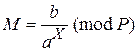Поскольку
, 
, то соотношение расшифрования справедливо.
Рассмотрим пример. Выберем Р = 11, G = 2, секретный ключ X = 8. Вычисляем 
. Итак, открытый ключ Y = 3. Пусть сообщение М = 5. Выберем некоторое случайное число
K = 9. Убедимся, что НОД (K, Р – 1) = 1. Действительно, НОД (9, 10) = 1. Вычисляем пару чисел а и b:
;
.
Получим шифртекст (a, b) = (6, 9).
Выполним расшифрование этого шифртекста. Вычисляем сообщение М, используя секретный ключ X:
.
Выражение М = 9/68 mod 11 можно представить в виде 
. Решая данное сравнение, находим М = 5.
В реальных схемах шифрования необходимо использовать в качестве модуля Р большое целое простое число, имеющее в двоичном представлении длину 512...1024 бит.
