Задание: Найти положение точки экстремума и экстремальное значение целевой функции  методом наискорейшего спуска (подъема) с точностью 0,001, если заданы координаты исходной точки
методом наискорейшего спуска (подъема) с точностью 0,001, если заданы координаты исходной точки  .
.
| № варианта | Вид целевой функции f(x) | Координаты исходной точки | Экстремум | ||
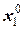
| 
| 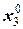
| |||
| x12 + x22- 0,5x1 - 1,6x2 + 2 | - | Min | |||
| x14 + x24 + 2x12x22 - 4x1 + 3 | - | Min | |||
| 3,2 - (x1 - 1)2 - (x2 - 3)2 – 4(x3 + 5)2 | -1 | Max | |||
| 1 – 2x1 - 2x2 - 4x1x2 + 10x12 + 2x22 | - | Min | |||
| (x12 + x2 - 8)2 + (x1 + x22 - 18)2 + 3 | - | Min | |||

| - | Min | |||
| (x1 - 2,4)2 + x22 – 3 | -2 | - | Min | ||
| x13 + 8x23 - 6x1x2 + 1 | - | Min | |||
| 4 - (x12 + x2 - 18)2 - (x1 + x22)2 | -2 | - | Max | ||

| - | Max | |||
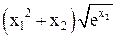
| -1 | -1 | - | Min | |
| (x1 + 0,5)2 + 2(x2 + 3,6)2 + (x3 - 1)4 + 1 | -5 | Min | |||
| x12 + x22 - 2(x1 + 2x2) + 7,35 | - | Min | |||
| X12 + x1x2 + x22 - 6x1 - 9x2 | - | Min | |||
| 6 - (x12 + x2 – 11)2 - (x1 + x22 - 7)2 | - | Max | |||
| x13 + x22 – 3x1 - 2x2 + 2 | - | Min | |||
| (x1 - 2)2 + 2x22 + 5,5 | - | Min | |||
| 4 - 4(x1 – 0,9)2 - 1,5(x2 + 1,6)4 - 0,8(x3 - 3,5)2 | -1 | -2 | Max | ||

| -3 | - | Min | ||
| x13 + x1x22 + 6x1x2 – 2 | -1 | -1 | - | Max | |

| - | Max | |||
| 4x12 + x22 – 12(x1 + x2) + 46 | - | Min | |||
| (x1 - 4)2 + 5(x2 + 3)2 + 7(x3 + 0,5)2 + 10 | -2 | Min | |||
| 2x12 + 3(x2 - 1,5)2 + 1 | -1 | - | Min | ||
| (x1 - 2,5)2 + (x2 + 4)2 + 8 | -1 | - | Min | ||

| - | Min | |||
| 4 – 2(x1 – 3)2 - (x2 - 2)2 – 3(x3 + 1)4 | -3 | Max | |||
| (x12 + x2)2 + (x1 + x22 - 18)2 + 4 | -2 | - | Min | ||
| (x12 + x2 - 7)2 + (x1 + x22 - 11)2 + 3 | - | Min | |||
| x12x2 + x23 + 6x1x2 + 1 | -1 | - | Max | ||
| 2(x1+2)2 + (x2-1.5)2 +3(x3-1)2 | -1 | Min | |||
| x12 + x1x2 + x22 –3x1 - 6x2 | -2 | - | Min | ||
| (x1-1)2 + (x2-3)2 + 4 | -3 | - | Min | ||
| 2x13 – x1x22 + 5x12 +3x22 + 2 | -1 | - | Min | ||
| x12 + x22 – 2x1 - 3x2 + 2 | - | Min | |||
| 6x1x2 - 8x13 - x23 – 3 | - | Max | |||
| x13 + x22 – 15x1x2 | - | Min | |||
| 2(x1 + x2 – x12) + 4x1x2 – 10x22 – 5 | -1 | - | Max | ||

| - | Min | |||

| Max | ||||
 
| - | Max | |||

| - | Max | |||

| -1 | - | Min | ||

| -1 | - | Min | ||

| - | Min | |||

| -1 | - | Min | ||

| -2 | - | Max | ||

| - | Max | |||

| -1 | -3 | Min | ||

| -2 | - | Min |
Вопросы для самоподготовки
1. В чем состоит общая задача нелинейного программирования?
2. На какие группы делятся методы решения задач безусловной минимизации?
3. Дайте краткую характеристику методов безусловной минимизации: итерационный характер методов; проблема выбора шага; выбор направления поиска.
4. Опишите алгоритм метода покоординатного спуска.
5. Как выбирается направление спуска в методе покоординатного спуска?
6. При выполнении какого условия следует прекратить поиск?
7. Составьте блок-схему метода покоординатного спуска.
8. Дайте сравнительную характеристику градиентных методов оптимизации.
9. Дайте описание алгоритма метода наискорейшего спуска.
10. Как решается проблема выбора шага и направления в методе наискорейшего спуска?
11. Дайте описание алгоритма метода сопряженных направлений.
12. В чем состоит основное отличие методов наискорейшего спуска и сопряженных направлений?
13. Какие методы условной минимизации вы знаете?
14. В чем главное отличие методов условной минимизации от методов безусловной минимизации?
15. Метод сканирования.
16. Каково минимальное количество вычислений целевой функции для метода сканирования?
17. Укажите область использования метода сканирования.
18. Метод штрафных функций.
19. На какие классы можно разделить методы штрафных функций?
20. Чем характеризуются параметрические методы?
Лабораторная работа № 10. Многомерный поиск. Линейное программирование
Задание: Найти положение точки экстремума и экстремальное значение целевой функции  при заданных ограничениях.
при заданных ограничениях.
| № варианта | Экстремум | a | b | c | Ограничения |
| Max | 2,1 | 5,5 | 1,4 |  ; ;  ; ;
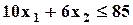 ; ;  ; ; 
| |
| Max | 3,0 | 0,9 | 1,8 | 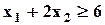 ; ;  ; ;  ; ;
 ; ; 
| |
| Min | 4,5 | 6,7 | 0,6 |  ; ; 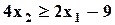 ; ;  ; ;  ; ; 
| |
 4 4
| Max | 0.8 | 5,4 | 3,1 |   ; ;  ; ;  ; ;  ; ; 
|
| Min | 1,9 | 2,6 | -1,2 |  ; ;  ; ;  ; ; 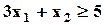 ; ; 
| |
| Min | 4,1 | 5,2 | 9,3 |  ; ;  ; ; 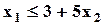 ; ;  ; ;  
| |
| Min | 5,4 | 1,5 | 5,7 |  ; ;  ; ;  ; ;
 ; ;  
| |
| Max | 3,8 | 2,9 | 1,3 |  ; ;  ; ;  ; ; 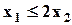 ; ; 
| |
| Max | 1,4 | 5,8 | 4,2 | 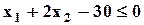 ; ;  ; ;  ; ;  ; ; 
| |
| Min | 4,6 | 1,1 | 6,5 |  ; ;  ; ;   ; ;  ; ; 
| |
| Max | 2,3 | 5,4 | 1,4 |  ; ;  ; ;  ; ;  ; ; 
| |
| Min | 6,5 | 1,7 | 0,9 |  ; ;  ; ; 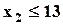 ; ;
 ; ; 
| |
| Max | 0,9 | 3,0 | 1,6 | 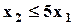 ; ;  ; ;   ; ; 
| |
| Max | 2,6 | 5,4 | 11,3 | 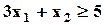 ; ;  ; ;  ; ;  ; ; 
| |
| Min | 6,4 | 2,5 | 0,9 |  ; ; 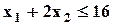 ; ;  ; ;  ; ; 
| |
| Max | 3,4 | 1,9 | 5,3 |  ; ;  ; ;  ; ;  ; ; 
| |
| Max | 1,8 | 3,2 | 1,5 |  ; ;  ; ;  ; ;  ; ; 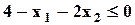
| |
| Min | 1,9 | 5,3 | 2,4 |  ; ;  ; ;  ; ;  ; ; 
| |
| Min | 2,6 | 8,4 | 1,3 |  ; ;  ; ;  ; ;  ; ; 
| |
| Min | 6,4 | 1,9 | 5,8 |  ; ;  ; ;  ; ;  ; ; 
| |
| Min | 5,2 | 4,1 | 9,3 |  ; ;  ; ;  ; ; 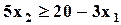 ; ; 
| |
| Max | 2,9 | 3,8 | 1.3 |  ; ; 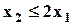 ; ; 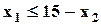 ; ;  ; ; 
| |
| Max | 5,8 | 1,4 | 3,8 |  ; ;  ; ;  ; ; 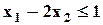 ; ; 
| |
| Min | 1,1 | 4,6 | 6,4 |  ; ;  ; ; 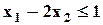 ; ;  ; ; 
| |
| Min | 1,5 | 4,6 | 2,3 |  ; ;  ; ;  ; ;  ; ; 
| |
| Max | 2,5 | 4,3 | 8,5 | 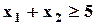 ; ;  ; ; 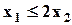 ; ; 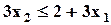 ; ; 
| |
| Max | 2,8 | 3,6 | 0,8 |  ; ;  ; ;  ; ;  ; ; 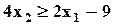 ; ;
| |
| Min | 6,4 | 3,0 | -5,4 |  ; ;  ; ;  ; ;  ; ; 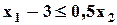
| |
| Max | 9,8 | 0,3 | 1,6 |  ; ;  ; ;  ; ;  ; ;  
| |
| Max | 2,0 | 2,5 | 3,6 |  ; ;  ; ; 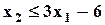 ; ;  ; ; 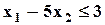
| |
| Min | 9.2 | 4.8 | 15.1 | 
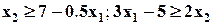
|
| Min | 3.2 | 1.1 | 0.4 | 
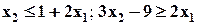
| |
| Min | 2.5 | 0.6 | 5.4 | 

| |
| Min | 5.5 | 0.7 | -3.5 | 

| |
| Max | 7.5 | 1.2 | 6.2 | 

| |
| Min | 1.4 | 2.9 | 4.4 | 
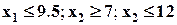
| |
| Max | 4.7 | 0.7 | 5.3 | 
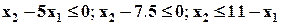
| |
| Min | 2.6 | 3.2 | 1.3 | 

| |
| Min | 1.8 | 4.2 | 1.5 | 

| |
| Max | 1.4 | 2.0 | 6.2 | 
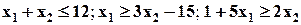
| |
| Max | 2.1 | 4.5 | 

| ||
| Min | 7.5 | 2.0 | 6.2 | 

| |
| Min | 1.3 | 4.2 | -1.5 | 

| |
| Min | 6.1 | 5.7 | 0.3 | 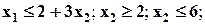

| |
| Max | 2.5 | 2.0 | 3.0 | 

| |
| Max | 1.2 | 7.5 | 6.0 | 

| |
| Min | 1.1 | 3.2 | 0.7 | 

| |
| Min | 0.6 | 2.5 | 5.5 | 

|
| Min | 8.7 | 1.6 | -4.5 | 
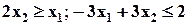
| |
| Max | 0.7 | 4.7 | 5.1 | 

|
Вопросы для самоподготовки
1. Что такое линейные модели?
2. Что понимается под линейным программированием?
3. Дайте математическую формулировку задачи линейного программирования.
4. Какие методы реализуют идею линейного программирования?
5. Графический метод.
6. Что называется областью допустимых решений?
7. Дайте характеристику вариантов области допустимых решений.
8. Симплексный метод решения задач линейного программирования.
Рекомендуемая литература
Основная:
1. Бахвалов Н. С. Численные методы. - М.: Наука. 1975.
2. Калиткин Н. Н. Численные методы. - М.: Наука. 1978.
3. Демидович Б. П., Марон И. А. Основы вычислительной математики. – М.:Наука, 1970.
4. Березин И. С., Жидков Н. П. Методы вычислений. – Ч.1: Наука, 1966; Ч.2: М.: Физматгиз, 1962.
Дополнительная:
1. Мак-Кракен Д., Дорн У. Численные методы и программирование на ФОРТРАНе. - М.: Мир, 1969.
2. Турчак Л. И. Основы численных методов. – М.: Высш. шк., 1985.
3. Воробьёва Г. Н., Данилова А. Н. Практикум по численным методам.– М.: Высш. шк., 1979.
4. Методы оптимизации. Методические указания и задания к практическим занятиям и лабораторным работам. / Сост. С. И. Смуров, Т. В. Сокольская, В. А. Бобкова. Иван. хим.-технол. ин-т, 1990. (№171)
5. Моделирование сложных изотермических реакций, описываемых линейными дифференциальными уравнениями. Методические указания. / Сост. С. И. Смуров, В. А. Таланова. Иван. хим.-технол. ин-т, 1992.(№211)
6. Методические указания и задания к практическим занятиям по численным методам / Сост. С. И. Смуров, Т. В. Сокольская. Иван. хим.-технол. ин-т, 1985.(№347)
7. Численные методы. Методические указания. / Сост. С. И. Смуров, В. А. Таланова, В. И. Шевченко. Иван. хим.-технол. ин-т, 1988.(№501)
Оглавление
Введение. 3
Лабораторная работа №1. Приближенное решение алгебраических и трансцендентных уравнений. 4
Лабораторная работа №2. Решение систем нелинейных уравнений. 6
Лабораторная работа №3. Численное интегрирование. 8
Лабораторная работа № 4. Решение систем линейных уравнения. 10
Лабораторная работа № 5. Математическая обработка экспериментальных данных. 13
Лабораторная работа № 6. Численное решение обыкновенных дифференциальных уравнений. 16
Лабораторная работа № 7. Численное решение дифференциальных уравнений в частных производных. 19
Лабораторная работа № 8. Методы одномерной оптимизации. 21
Лабораторная работа № 9. Многомерный поиск. Методы безусловной минимизации. 24
Лабораторная работа № 10. Многомерный поиск. Линейное программирование. 27
Рекомендуемая литература. 31
Редактор В. Л. Родичева
Подписано в печать. Формат  . Бумага писчая. Печать плоская. Усл. печ. л. 2,09. Уч. - изд. л. 2,32. Тираж экз. Заказ
. Бумага писчая. Печать плоская. Усл. печ. л. 2,09. Уч. - изд. л. 2,32. Тираж экз. Заказ
Ивановский государственный химико-технологический университет
153460, г. Иваново, пр. Ф. Энгельса, 7.






