Задание: Используя метод Ньютона, решить систему нелинейных уравнений с точностью до  .
.
| № варианта | Система | № варианта | Система |

| 
| ||

| 
| ||

| 
| ||
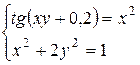
| 
| ||

| 
| ||

| 
| ||
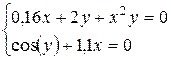
| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 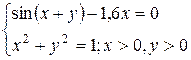
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 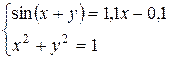
| ||

| 
| ||
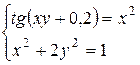
| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
|
Вопросы для самоподготовки
1. Условия применимости метода Ньютона.
2. Вывод основной формулы.
3. Условия окончания вычислений.
Лабораторная работа №3. Численное интегрирование
Задание: Вычислить определенный интеграл  с точностью
с точностью 
| № | а | b | f(x) | № | а | b | f(x) |
| 0,6 | 1,5 |

| 1,2 | 
| |||
| 1,2 | 2,832 | 
| 1,6 | 2,4 | 
| ||
| 1,3 | 2,956 |

| 0,2 | 
| |||
| 2,8 | 4,408 | 
| 0,6 | 1,4 | 
| ||
| 0,8 | 2,528 | 
| 0,4 | 1,2 |

| ||
| -0,52 | 1,58 | 
| 0,8 | 1,2 | 
| ||
| 0,2 | 2,12 | 
| 0,8 | 1,6 | 
| ||
| 1,5 | 3,42 | 
| 0,4 | 1,2 | 
| ||
| 1,1 | 2,876 | 
| 0,4 | 1,2 |

| ||
| 0,31 | 1,93 | 
| 0,4 | 
| |||
| 1,5 | 3,18 | 
| 0,18 | 0,98 | 
| ||
| -1,3 | 0,476 | 
| 1,4 |

| |||
| 1,0 | 2,76 | 
| 1,4 | 2,2 | 
| ||
| 2,4 | 4,08 | 
| 0,4 | 1,2 | 
| ||
| 1,82 | 3,464 | 
| 0,8 | 1,6 | 
| ||
| 1,5 | 3,24 | 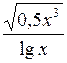
| 0,6 | 1,4 |

| ||
| 1,4 | 3,008 | 
| 1,2 | 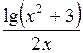
| |||
| -0,2 | 1,252 | 
| 2,5 | 3,3 | 
| ||
| 0,15 | 1,878 | 
| 0,5 | 1,2 | 
| ||
| -0,52 | 1,58 | 
| 1,3 | 2,1 | 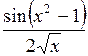
| ||
| 0,3 | 1,844 | 
| 0,2 | 1,0 | 
| ||
| 3,5 | 4,94 | 
| 0,8 | 1,2 | 
| ||
| 1,44 | 
| 1,2 | 2,8 | 
| |||
| 5,1 | 6,54 | 
| 0,6 | 0,72 | 
| ||
| 1,42 | 2,98 | 
| 0,8 | 1,2 | 
|
Вопросы для самоподготовки
1. Геометрический смысл определённого интеграла.
2. Общая идея методов численного интегрирования.
3. Методы левых, правых, средних прямоугольников (формулы, геометрическая иллюстрация, оценка погрешности).
4. Метод трапеций (формула, геометрическая иллюстрация, оценка погрешности).
5. Метод Симпсона (формула, геометрическая иллюстрация, оценка погрешности).
6. Правило Рунге.
7. Сравнительная оценка методов численного интегрирования.
Лабораторная работа № 4. Решение систем линейных уравнения
Задание: Методом простой итерации или методом Зейделя решить систему линейных уравнений с точностью  =10-3.
=10-3. 

| № | Система | № | Система |

| 
| ||

| 
| ||
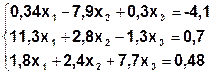
| 
| ||

| 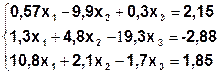
| ||

| 
| ||

| 
| ||

| 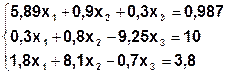
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 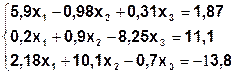
| ||

| 
| ||

| 
| ||

| 
| ||
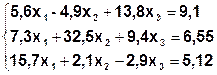
| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 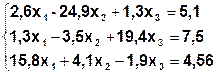
| ||

| 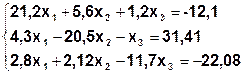
|
Вопросы для самоподготовки
- Вывод расчетной формулы метода простой итерации.
- Вывод расчетной формулы метода Зейделя.
- Условия сходимости и условия окончания вычислительного процесса.
- Сравнительная характеристика методов решения систем линейных уравнений (точных и приближенных).
Лабораторная работа № 5. Математическая обработка экспериментальных данных
Задание: Для функции, заданной таблично, подобрать эмпирическую зависимость и найти параметры приближающей функции методом наименьших квадратов.
| №1 | x | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 |
| y | 3,030 | 3,142 | 3,358 | 3,463 | 3,772 | 3,251 | 3,170 | 3,665 | |
| №2 | x | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 |
| y | 3,314 | 3,278 | 3,262 | 3,292 | 3,332 | 3,397 | 3,487 | 3,563 | |
| №3 | x | 2,0 | 2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,7 | |
| y | 1,045 | 1,162 | 1,264 | 1,172 | 1,070 | 0,898 | 0,656 | 0,344 | |
| №4 | x | 0,3 | 0,6 | 0,9 | 1,2 | 1,5 | 1,8 | 2,1 | 2,4 |
| y | 6,715 | 6,735 | 6,750 | 6,741 | 6,645 | 6,639 | 6,647 | 6,612 | |
| №5 | x | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | 2,6 |
| y | 2,325 | 2,515 | 2,638 | 2,700 | 2,696 | 2,626 | 2,491 | 2,291 | |
| №6 | x | 2,1 | 2,3 | 2,5 | 2,7 | 2,9 | 3,1 | 3,3 | 3,5 |
| y | 1.752 | 1,762 | 1,777 | 1,797 | 1,821 | 1,850 | 1,884 | 1,944 | |
| №7 | x | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 | 2,1 | 2,2 |
| y | 1,924 | 1,710 | 1,525 | 1,370 | 1,264 | 1,190 | 1,148 | 1,127 | |
| №8 | x | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 |
| y | 1,025 | 1,144 | 1,336 | 1,419 | 1,479 | 1,530 | 1,568 | 1,248 | |
| №9 | x | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 | 2,7 | 2,8 | 2,9 |
| y | 5,785 | 5,685 | 5,605 | 5,545 | 5,505 | 5,480 | 5,495 | 5,510 | |
| №10 | x | 0,5 | 0,7 | 0,9 | 1,1 | 1,3 | 1,5 | 1,7 | 1,9 |
| y | 4,052 | 4,092 | 4,152 | 4,234 | 4,338 | 4,468 | 4,599 | 4,771 | |
| №11 | x | 0,3 | 0,5 | 0,7 | 0,9 | 1,1 | 1,3 | 1,5 | 1,7 |
| y | 0,344 | 0,364 | 0,374 | 0,372 | 0,350 | 0,328 | 0,296 | 0,256 | |
| №12 | x | 0,4 | 0,6 | 0,8 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 |
| y | 0,205 | 0,235 | 0,249 | 0,245 | 0,225 | 0,190 | 0,140 | 0,076 | |
| №13 | x | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 |
| y | 1,044 | 1,161 | 1,203 | 1,172 | 1,076 | 0,856 | 0,654 | 0,342 | |
| №14 | x | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 |
| y | 0,525 | 0,625 | 0,678 | 0,681 | 0,640 | 0,552 | 0,492 | 0,362 | |
| №15 | x | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 |
| y | 4,230 | 4,253 | 4,256 | 4,240 | 4,205 | 4,150 | 4,075 | 3,980 | |
| №16 | x | 2,0 | 2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 | 2,7 |
| y | 5,022 | 5,143 | 5,195 | 5,175 | 5,085 | 4,925 | 4,705 | 4,406 |
| №17 | x | 3,0 | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 | 3,7 |
| y | 1,125 | 1,175 | 1,21, | 1,237 | 1,251 | 1,255 | 1,242 | 1,223 | |
| №18 | x | 2,0 | 2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 | 2,7 |
| y | 1,220 | 1,253 | 1,256 | 1,232 | 1,175 | 1,091 | 0,985 | 0,850 | |
| №19 | x | 0,5 | 0,7 | 0,9 | 1,1 | 1,3 | 1,5 | 1,7 | 1,9 |
| y | 3,150 | 3,171 | 3,181 | 3,179 | 3,165 | 3,140 | 3,105 | 3,059 | |
| №20 | x | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 |
| y | 4,018 | 4,025 | 4,035 | 4,048 | 4,012 | 4,028 | 4,015 | 4,002 | |
| №21 | x | -4,3 | -4,0 | -3,8 | -3,1 | -2,1 | -0,8 | -0,5 | 0,4 |
| y | 3,421 | 2,331 | 0,624 | -0,963 | -1,843 | -1,020 | 0,114 | 2,713 | |
| №22 | x | -3,3 | -3,0 | -2,8 | -2,1 | -1,1 | 0,2 | 0,5 | 1,4 |
| y | 1,920 | 0.330 | -1,471 | -2,962 | -3,840 | -3,023 | -1,884 | 0,713 | |
| №23 | x | -1,3 | -1,0 | -0,8 | -0,1 | 0,9 | 2,2 | 2,5 | 3,4 |
| y | 4,921 | 3,330 | 1,624 | 0,028 | -0,840 | -0,025 | 1,116 | 3,713 | |
| №24 | x | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 | 3,7 | 3,8 |
| y | 2,527 | 2,635 | 2,655 | 2,563 | 2,361 | 2,048 | 1,638 | 1,118 | |
| №25 | x | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 |
| y | 4,030 | 4,142 | 4,251 | 4,958 | 4,478 | 4,593 | 4,465 | 4,362 | |
| №26 | x | 0,7 | 0,9 | 1,1 | 1,3 | 1,5 | 1,7 | 1,9 | 2,1 |
| y | 5,715 | 5,735 | 5,750 | 5,741 | 5,647 | 5,649 | 5,644 | 5,636 | |
| №27 | x | -3,3 | -3,0 | -2,7 | -2,4 | -2,1 | -1,8 | -1,5 | -1,2 |
| y | 2,920 | 1,331 | -0,476 | -1,968 | -2,841 | -2,021 | -0,881 | 1,713 | |
| №28 | x | -4,3 | -4,0 | -3,8 | -3,1 | -2,1 | -0,8 | -0,5 | 0,4 |
| y | 5,921 | 4,330 | 2,623 | 1,030 | 0,157 | 0,979 | 2,114 | 4,714 | |
| №29 | x | 0,8 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 |
| y | 1,325 | 1,515 | 1,638 | 1,700 | 1,692 | 1,626 | 1,491 | 1,290 | |
| №30 | x | 2,1 | 2,3 | 2,5 | 2,7 | 2,9 | 3,1 | 3,3 | 3,5 |
| y | 3,325 | 3,515 | 3,637 | 3,700 | 3,695 | 3,625 | 3,491 | 3,291 | |
| №31 | x | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 |
| y | 0,344 | 0,364 | 0,374 | 0,372 | 0,350 | 0,328 | 0,296 | 0,256 | |
| №32 | x | 0,3 | 0,5 | 0,7 | 0,9 | 1,1 | 1,3 | 1,5 | 1,7 |
| y | 0,525 | 0,625 | 0,678 | 0,681 | 0,640 | 0,552 | 0,492 | 0,362 | |
| №33 | x | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | 2,6 |
| y | 1,752 | 1,762 | 1,777 | 1,797 | 1,821 | 1,850 | 1,884 | 1,944 | |
| №34 | x | 2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 | 2,7 | 2,8 |
| y | 2,785 | 2,685 | 2,605 | 2,545 | 2,505 | 2,485 | 2,490 | 2,515 | |
| №35 | x | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | 2,6 |
| y | 1,924 | 1,710 | 1,525 | 1,370 | 1,264 | 1,190 | 1,148 | 1,127 | |
| №36 | x | -2,3 | -2,0 | -1,8 | -1,1 | -0,1 | 1,2 | 1,5 | 2,4 |
| y | 2,527 | 2,635 | 2,655 | 2,563 | 2,361 | 2,048 | 1,638 | 1,118 | |
| №37 | x | -1,3 | -1,0 | -0,8 | -0,1 | 0,9 | 2,2 | 2,5 | 3,4 |
| y | 0,525 | 0,625 | 0,678 | 0,681 | 0,640 | 0,552 | 0,492 | 0,362 | |
| №38 | x | 2,0 | 2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 | 2,7 |
| y | 5,921 | 4,330 | 2,623 | 1,030 | 0,157 | 0,979 | 2,114 | 4,714 | |
| №39 | x | 0,8 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 |
| y | 4,018 | 4,025 | 4,035 | 4,048 | 4,012 | 4,028 | 4,015 | 4,002 | |
| №40 | x | 3,0 | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 | 3,7 |
| y | 5,715 | 5,735 | 5,750 | 5,741 | 5,647 | 5,649 | 5,644 | 5,636 | |
| №41 | x | -3,3 | -3,0 | -2,7 | -2,4 | -2,1 | -1,8 | -1,5 | -1,2 |
| y | 1.752 | 1,762 | 1,777 | 1,797 | 1,821 | 1,850 | 1,884 | 1,944 | |
| №42 | x | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | 2,6 |
| y | 3,325 | 3,515 | 3,637 | 3,700 | 3,695 | 3,625 | 3,491 | 3,291 | |
| №43 | x | 2,1 | 2,3 | 2,5 | 2,7 | 2,9 | 3,1 | 3,3 | 3,5 |
| y | 1,220 | 1,253 | 1,256 | 1,232 | 1,175 | 1,091 | 0,985 | 0,850 | |
| №44 | x | -1,3 | -1,0 | -0,8 | -0,1 | 0,9 | 2,2 | 2,5 | 3,4 |
| y | 4,230 | 4,253 | 4,256 | 4,240 | 4,205 | 4,150 | 4,075 | 3,980 | |
| №45 | x | 0,5 | 0,7 | 0,9 | 1,1 | 1,3 | 1,5 | 1,7 | 1,9 |
| y | 5,022 | 5,143 | 5,195 | 5,175 | 5,085 | 4,925 | 4,705 | 4,406 | |
| №46 | x | 3,0 | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 | 3,7 |
| y | 0,525 | 0,625 | 0,678 | 0,681 | 0,640 | 0,552 | 0,492 | 0,362 | |
| №47 | x | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | 2,6 |
| y | 1,325 | 1,515 | 1,638 | 1,700 | 1,692 | 1,626 | 1,491 | 1,290 | |
| №48 | x | -3,3 | -3,0 | -2,7 | -2,4 | -2,1 | -1,8 | -1,5 | -1,2 |
| y | 1,045 | 1,162 | 1,264 | 1,172 | 1,070 | 0,898 | 0,656 | 0,344 | |
| №49 | x | -1,3 | -1,0 | -0,8 | -0,1 | 0,9 | 2,2 | 2,5 | 3,4 |
| y | 4,030 | 4,142 | 4,251 | 4,958 | 4,478 | 4,593 | 4,465 | 4,362 | |
| №50 | x | 2,3 | 2,4 | 2,5 | 2,6 | 2,7 | 2,8 | 2,9 | 3,0 |
| y | 3,030 | 3,142 | 3,251 | 3,358 | 3,468 | 3,563 | 3,647 | 3,762 |
Вопросы для самоподготовки
1. Математическая постановка задачи интерполирования.
2. Линейная интерполяция.
3. Интерполяционный полином Лагранжа.
4. Постановка задачи математической обработки данных с помощью метода наименьших квадратов. Геометрическая интерпретация метода.
5. Нахождение параметров линейной приближающей функции.
6. Нахождение параметров квадратичной приближающей функции.
7. Нахождение параметров степенной и показательной приближающих функций.
Лабораторная работа № 6. Численное решение обыкновенных дифференциальных уравнений
Задание: Найти численное решение задачи Коши для данного дифференциального уравнения и начального условия  на отрезке
на отрезке  с шагом
с шагом  . Использовать метод, указанный преподавателем.
. Использовать метод, указанный преподавателем.
| № варианта | Уравнение | Начальное условие | a | b |

| 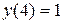
| |||
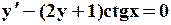
| 
| 
| 
| |

| 
| -1 | -0,1 | |

| 
| 
| 
| |

| 
| |||

| 
| |||

| 
| |||

| 
| -1 | -0,1 | |

| 
| |||

| 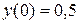
| |||

| 
| |||

| 
| |||

| 
| |||

| 
| |||
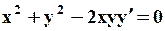
| 
| |||
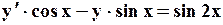
| 
| |||

| 
| |||

| 
| 1,6 | 2,6 | |

| 
| 0,2 | 1,2 | |

| y(0)=0 | |||

| y(0)=0 | |||

| y(1)=2 | |||
 
| y(0)=0 | |||

| y(0)=0 | |||

| y(0)=0 | |||

| y(1,2)=1 | 1,2 | 2,2 | |

| y(0)=0 | |||

| y(1)=1 | |||

| y(0)=0 | |||

| y(1)=1 | |||

| y(0)=0 | |||

| y(2)=2 | |||

| y(0)=0 | |||

| y(0)=0 | |||

| y(1)=1 | |||

| y(0)=0 | |||

| y(0)=0 | |||

| y(2)=1 | |||

| y(0)=0 | |||

| y(0)=0 | |||

| y(1)=1 | |||

| y(0)=0 | |||

| y(1,5)=1 | 1,5 | 2,5 | |

| y (0)=0,2 | |||

| y(0)=0,5 | |||

| y(0)=0 | |||

| y(1)=2 | |||

| y(0)=0 | |||

| y(0)=0,3 | |||

| y(0)=0,7 |
Вопросы для самоподготовки
1. Общая постановка задачи Коши.
2. Что является решением задачи Коши? Каков его геометрический смысл?
3. В чём состоит численное решение задачи Коши?
4. Метод Эйлера (алгоритм, геометрическая интерпретация, программа).
5. Метод Рунге-Кутта второго порядка (алгоритм, геометрическая интерпретация, программа).
6. Метод Эйлера-Коши (алгоритм, геометрическая интерпретация, программа).






