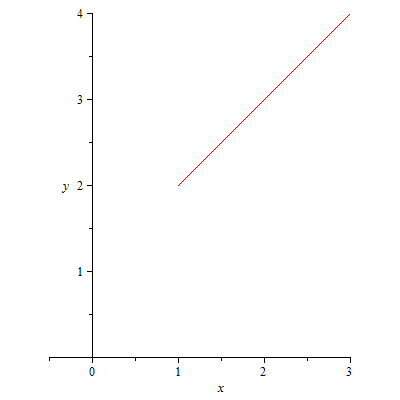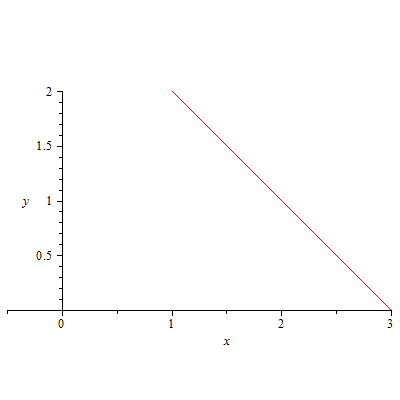157. 
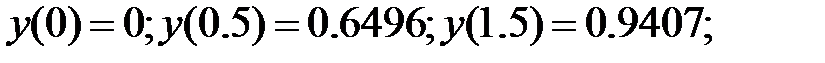
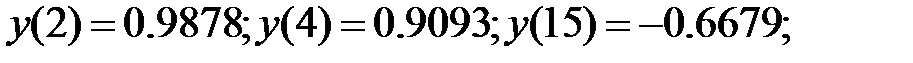
158. 
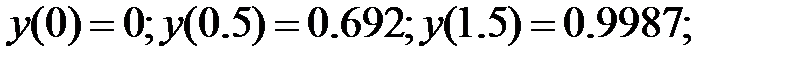
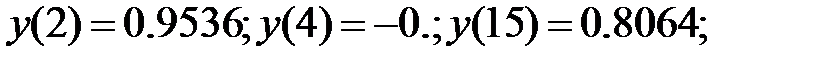
159. 1)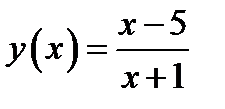 
; 2) 
;
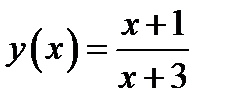160.1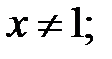 
160.2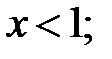 
160.3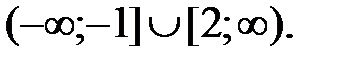 
160.4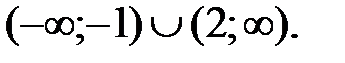 
161.1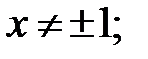 
161.2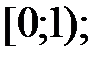 
161.3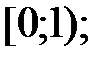 
161.4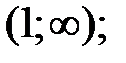 
. 161.5 
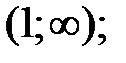161.6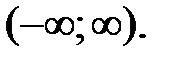 
162.1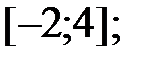 
161.2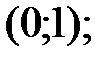 
161.3 (0;1).
163.1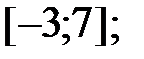 
163.2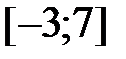 
163.3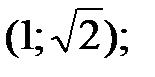 
163.4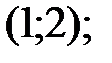 
163.5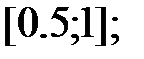 
163.6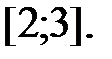 
164.1 утверждение верно; 164.2 неверно.
165.1.1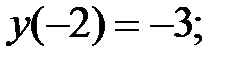 
165.1.2 
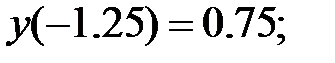165.1.3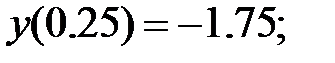 
165.1.4 
165.1.5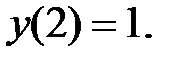 
165.2.1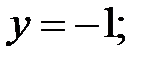 
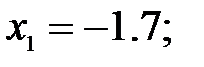
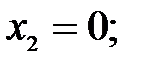
165.2.2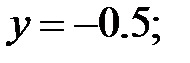 
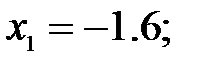
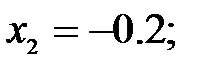
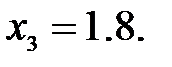
165.2.3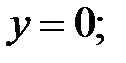 
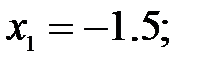
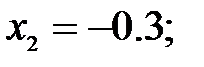
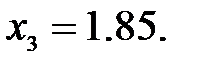165.2.4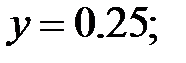 
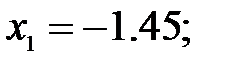
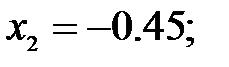
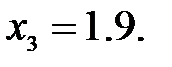165.2.5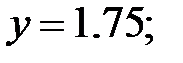 
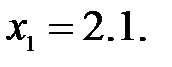
168. 1) функции различны т.к. у них разные области определения;
2) функции совпадают на указанной области определения;
3) функции различны т.к. у них разные области определения;
4) функции совпадают на указанной области определения.
169. 1) функции совпадают на указанной области определения;
2) функции различны;
3) функции совпадают на указанной области определения;
4) функции различны;
5) функции совпадают на указанной области определения;
6) функции различны;
7) функции совпадают на указанной области определения.
170. 1) четная; 2) четная; 3) четная; 4) нечетная.
171. 1) нечетная; 2) нечетная; 3) четная; 4) нечетная.
172. 1) четная; 2) общего вида; 3) общего вида; 4) общего вида; 5) общего вида;
6) четная; 7) общего вида; 8) нечетная; 9) четная; 10) общего вида; 11) четная;
12) четная; 13) четная; 14) нечетная; 15) четная.
173.1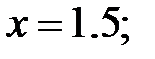 
173.2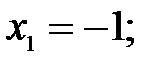 
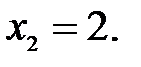173.3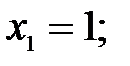 
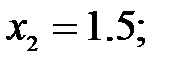173.4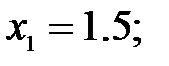 
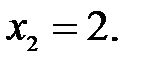
174. 1) Пусть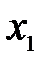 
> 
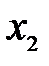, составим разность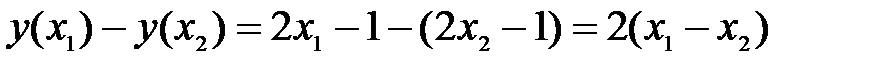 
следовательно,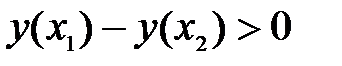 
т.е. функция возрастает.
2) Пусть 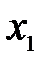> 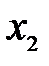составим разность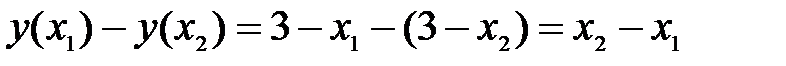 
следовательно,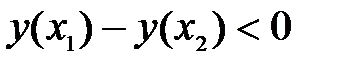 
т.е. функция убывает.
175. 1) убывает; 2) убывает; 3) убывает; 4) немонотонна; 5) убывает; 6) возрастает; 7) немонотонна; 8) возрастает; 9)немонотонна; 10) убывает.
176.1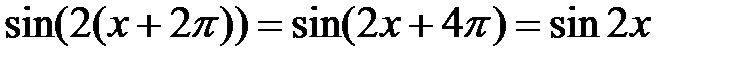 
, следовательно, 
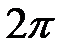период.
176.2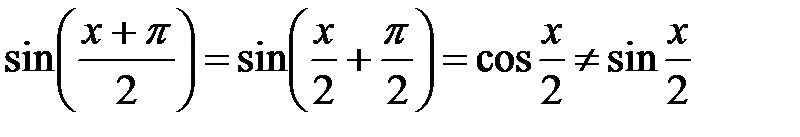 
, следовательно, 
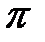не является периодом.
176.3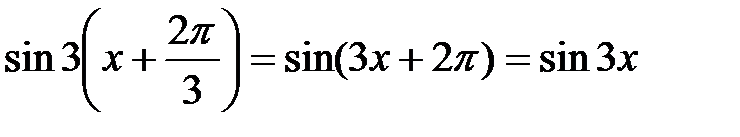 
, следовательно, 
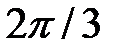период.
177. 1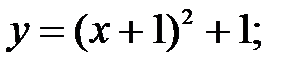 
минимум функции достигается при 
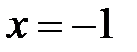и равен 1.
177.2 Максимум функции равен 7 и достигается при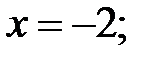 
177.3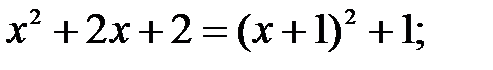 
т.к. функция 
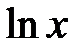монотонно возрастает, то
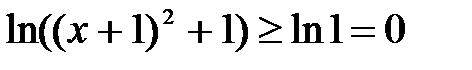, значит экстремум исходной функции равен 0.
178.1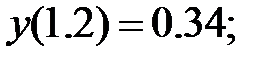 
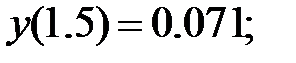
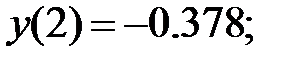
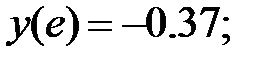
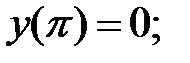
178.2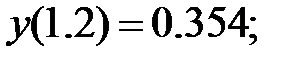 
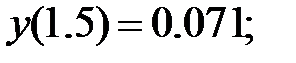
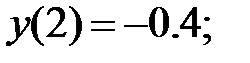
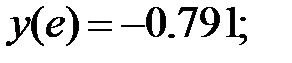
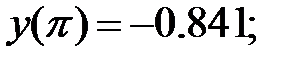
178.3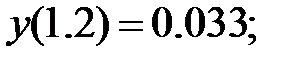 
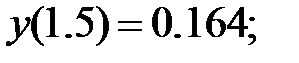
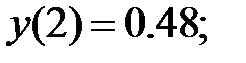
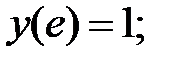
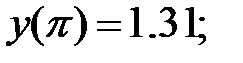
178.4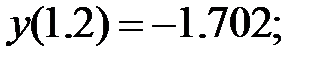 
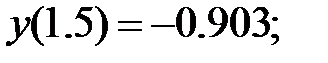
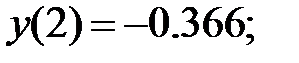
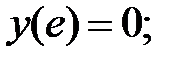
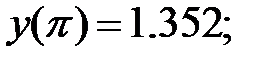
180.1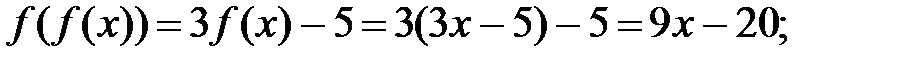 
180.2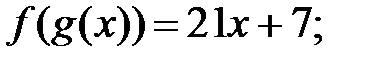 
180.3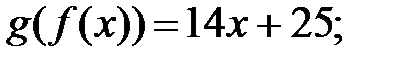 
180.4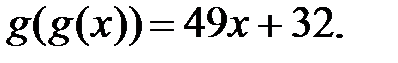 
181.1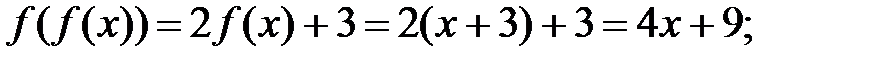 
181.2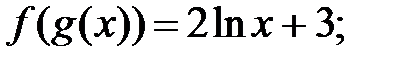 
181.3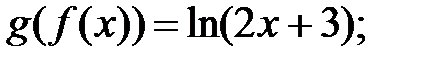 
181.4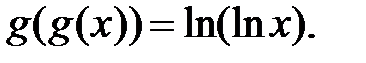 
182.1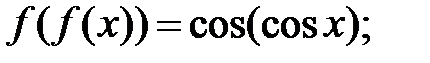 
182.2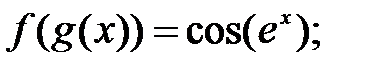 
182.3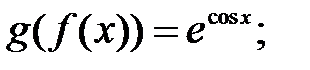 
182.4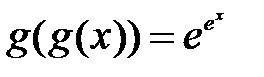 
. 183. Изисходной функции 
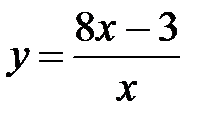выразим х:
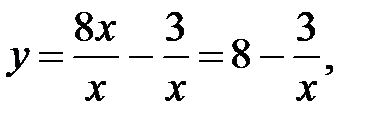
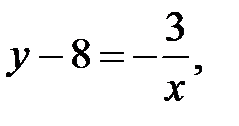
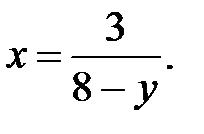Следовательно, обратная функция имеет вид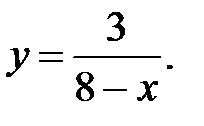 
184. Изисходной функции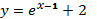 
выразим x:
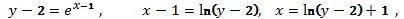
следовательно, обратная функция имеет вид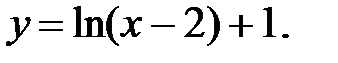 
185.1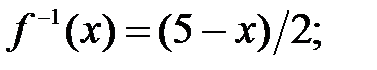 
185.2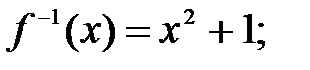 
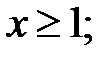
185.3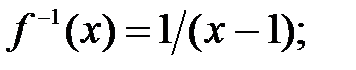 
185.4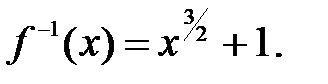 
187. 
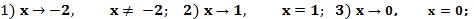
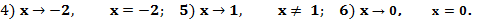
188. 
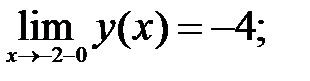
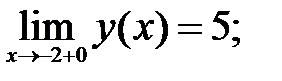
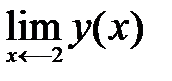- не существует.
189.1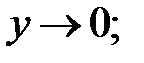 
189.2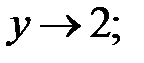 
189.3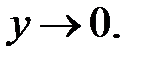 
190.1 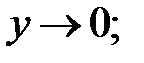190.2 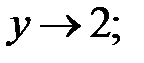190.3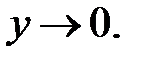 
191.1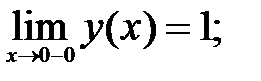 
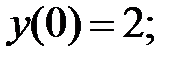
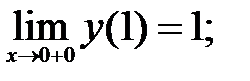предельного значения нет.
191.2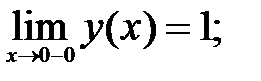 
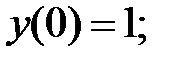
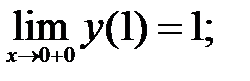предельное значение 
.
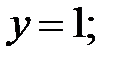191.3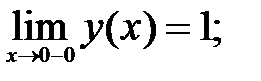 
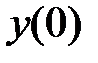-не определено; 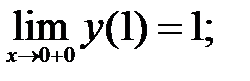предельного значения нет.
192.1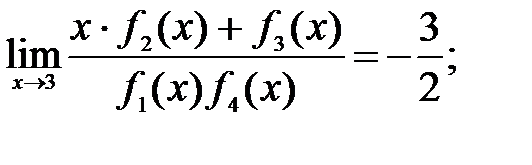 
192.2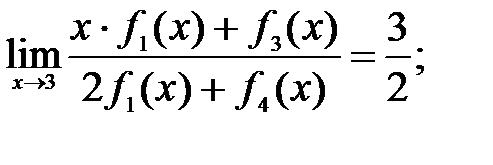 
192.3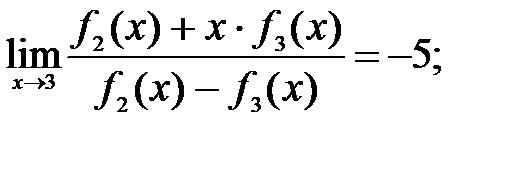 
192.4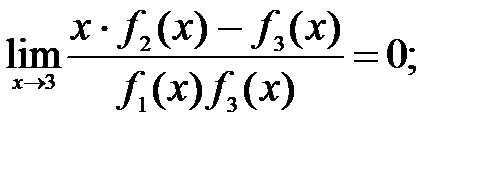 
193.1 -52; 193.2 14; 193.3 0.4; 193.4 1; 193.5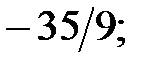 
193.6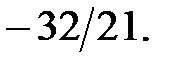 
194.1 -1777/60; 194.2 197/12; 194.3 -4/3; 194.4 4.5; 194.5 -3.4; 194.6 -1.2.
195.1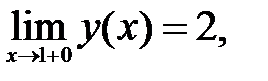 
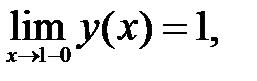
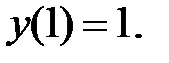
195.2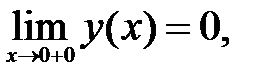 
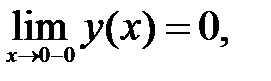
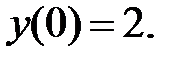
195.3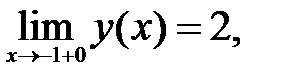 
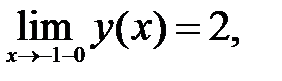
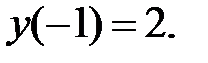
196. 
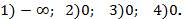
197. 
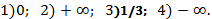
198. 
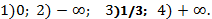
199.1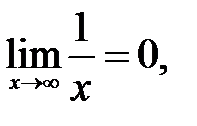 
следовательно, 
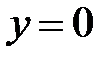- горизонтальная асимптота.
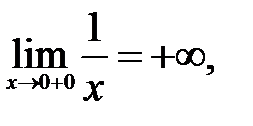следовательно, 
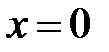- вертикальная асимптота.
199.2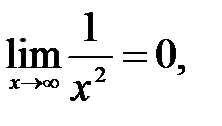 
следовательно, 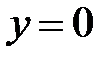- горизонтальная асимптота.
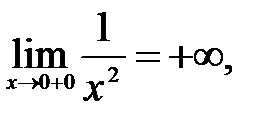следовательно, 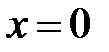- вертикальная асимптота.
200.1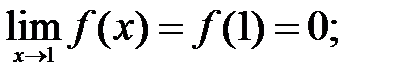 
200.2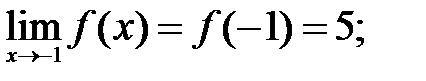 
200.3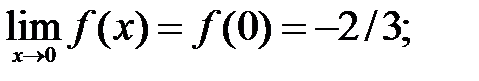 
200.4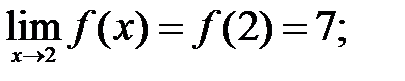 
200.5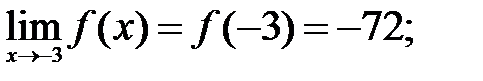 
200.6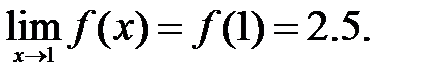 
201. 1) 2; 2) 0; 3) -2,5; 4) 3; 5) 0; 6) 1,5. 202. 1) -0,5; 2) 0; 3) 1; 4) 2; 5) 0; 6)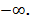 
203.1 5; 203.2 --5; 203.3 5/6; 203.4 0.25; 203.5 -1.5; 203.6 4; 203.7 -3; 203.8 0.8;
203.9 0.5; 203.10 0.25; 203.11 -2/3; 203.12 -0.75.
204. 1)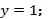 
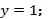2) 3) 
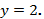
205.1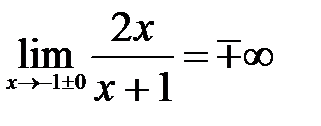 
, следовательно, 
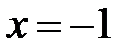- вертикальная асимптота;
205.2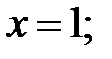 
205.3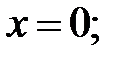 
205.4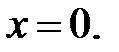 
206. Так как функции 
и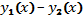 
непрерывны по условию, то их сумма и разность также непрерывны, следовательно, и непрерывны 
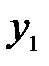и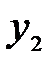 
.
207.1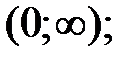 
207.2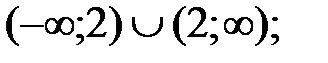 
207.3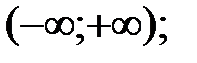 
207.4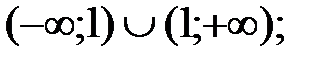 
207.5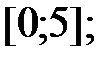 
207.6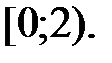 
208. 1) 2; 2) 2.
209. 1)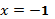 
точка разрыва 2-го рода; 2) 
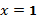точка разрыва 2-го рода;
3) функция определена и непрерывна на всей числовой прямой;
4) 
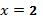точка разрыва 2-го рода; 5) 
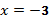точка разрыва 2-го рода;
6) 
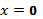точка разрыва 1-го рода, устранимый разрыв.
210. 1)В точке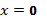 
функция терпит разрыв первого рода (скачок); в точке
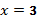функция непрерывна;
2) в точке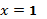 
функция терпит разрыв первого рода (скачок); в точке
функция непрерывна;
3) в точке 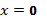функция терпит разрыв первого рода (скачок); в точке
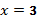функция непрерывна;
4) в точке функция терпит разрыв первого рода (скачок); в точке
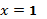функция непрерывна.
211. На интервалах 
функция достигает своего наибольшего и наименьшего значений.
212.1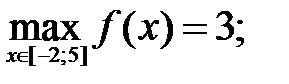 
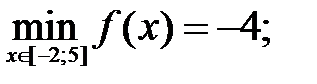212.2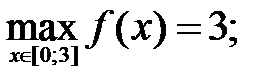 
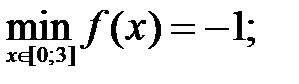
212.3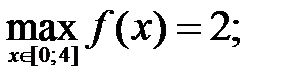 
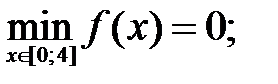212.4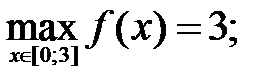 
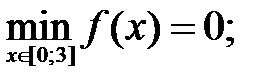
213. 1) 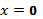- точка разрыва второго рода;
2) функция непрерывна;
3) 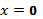- точка разрыва второго рода;
4) функция не определена.
214. В общем виде многочлен третьего порядка имеет вид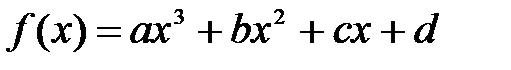 
.
Поскольку функция определена на всей числовой прямой и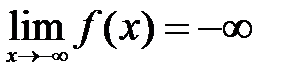 
,
(будем считать, для определенности, что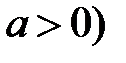 
, а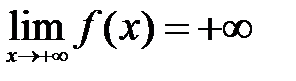 
, то существует хотя бы одна точка 
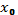такая, что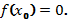 
215.1 1; 215.2 3/7; 215.3 1; 215.4 1; 215.5 8; 215.6 6; 215.7 2; 215.8 1; 215.9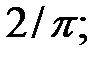 
215.10 0; 215.11 1/3; 215.12 е2; 215.13 3; 215.14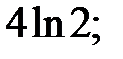 
215.15 
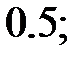215.16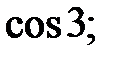 
215.17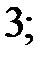 
215.18 1; 215.19 
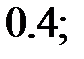215.20 
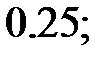215.21 5/6.
216. 1) е 2)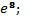 
3) 
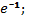4) 1; 5) 1/7. 217. 1) 
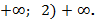218. 1) 1; 2) 1; 3) 1; 4)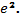 
219. 1)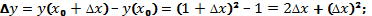 
2) 
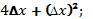3) 
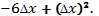
220.1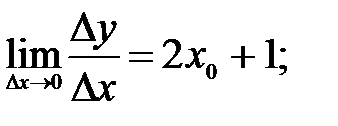 
220.2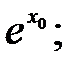 
220.3 
220.4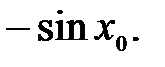 
221. 1) уравнение касательной: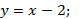 
уравнение нормали: 
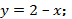точки пересечения касательной с осями координат: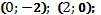 
2) уравнение касательной: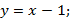 
уравнение нормали: 
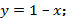точки пересечения касательной с осями координат: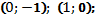 
3) уравнение касательной: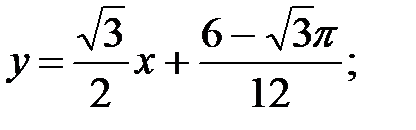 
уравнение нормали: 
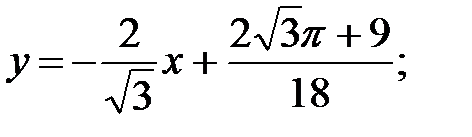точки пересечения касательной с осями координат: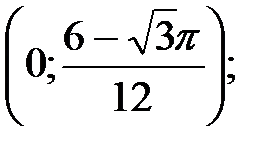 
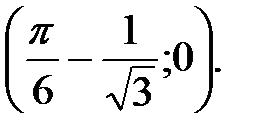
222. В точке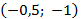 
угловой коэффициент 
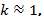следовательно, касательная имеет вид: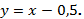 
В точке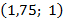 
угловой коэффициент 
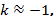следовательно, уравнение касательной имеет вид: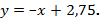 
223.1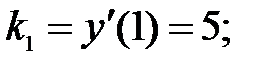 
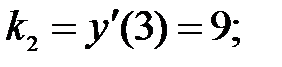
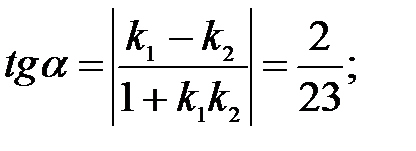
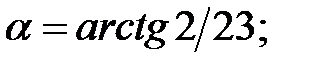
223.2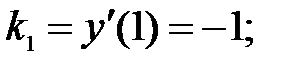 
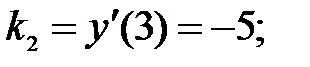
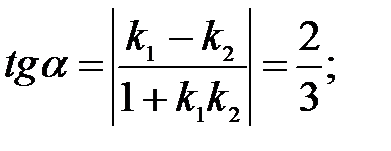
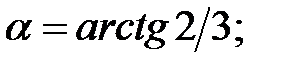
223.3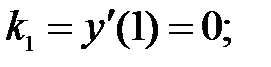 
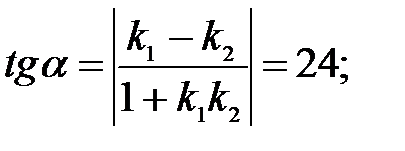
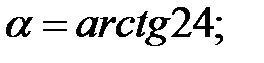
224.1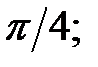 
224.2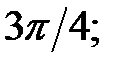 
224.3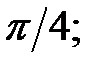 
224.4 
225. 1) Графики функци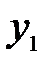й 
и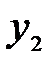 
пересекаются в двух точках с абсциссами 
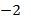и х=3.
Острый угол между графиками этих функций в точке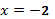 
равен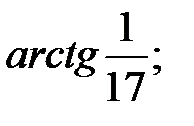 
в точке 
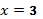угол равен 
.
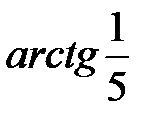2) Графики функци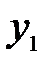й и 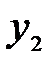пересекаются в точке с абсциссой 0 под углом 
3) Графики функци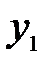й и 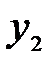пересекаются в точке с абсциссой 1 под углом
226. 
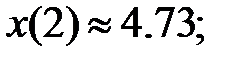
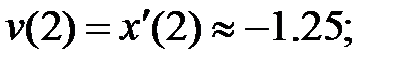
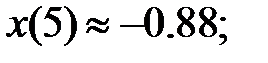
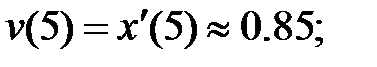
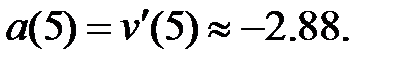
226.1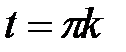 
226.2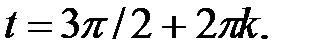 
227.1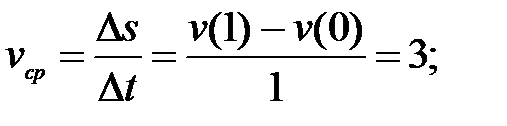 
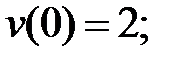
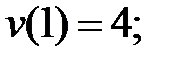227.2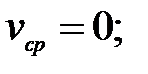 
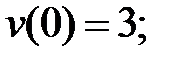
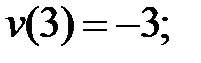
227.3 
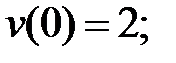
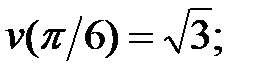227.4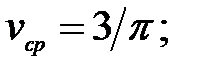 
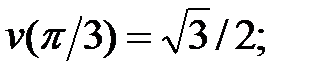
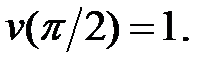
228. Скорости совпадают т.е.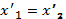 
при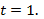 
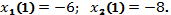
229.1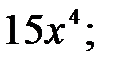 
229.2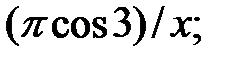 
229.3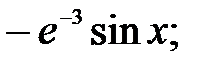 
229.4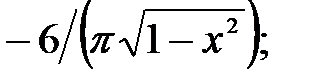 
229.5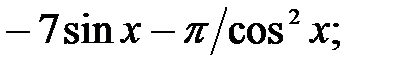 
229.6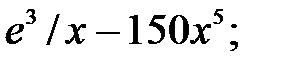 
229.7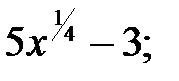 
229.8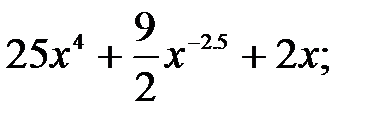 
229.9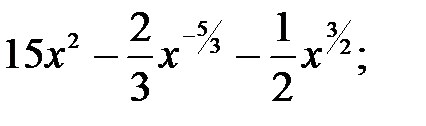 
229.10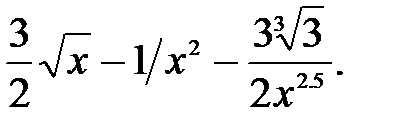 
230.1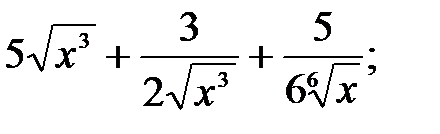 
230.2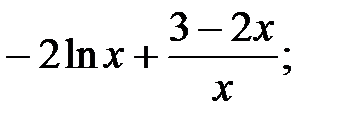 
230.3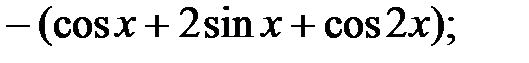 
230.4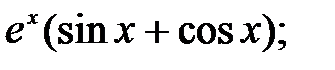 
230.5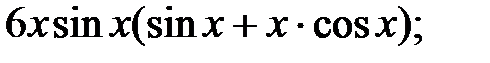 
230.6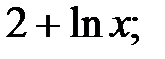 
230.7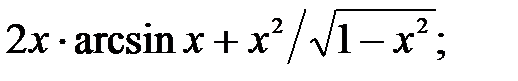 
230.8.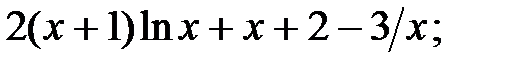 
230.9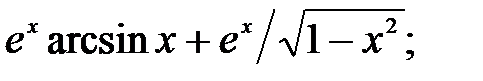 
230.10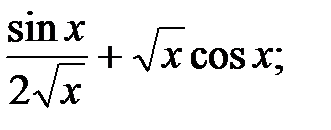 
230.11 
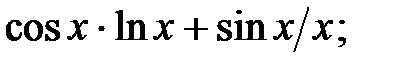230.12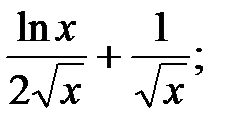 
230.13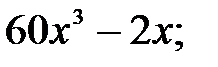 
230.14 
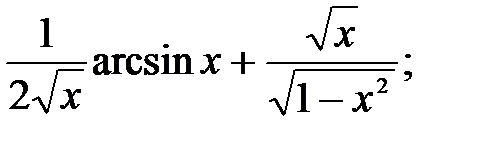230.15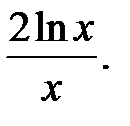 
231.1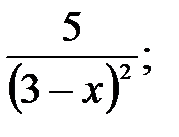 
231.2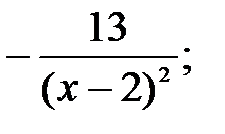 
231.3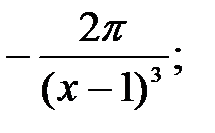 
231.4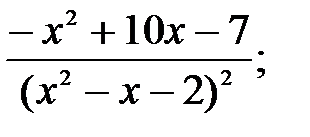 
231.5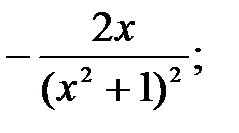 
231.6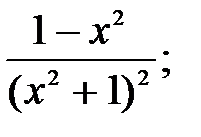 
231.7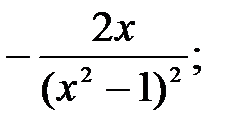 
231.8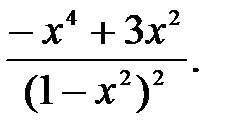 
232. 
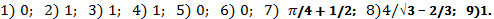
233. 1 
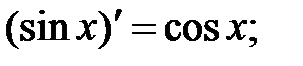233.2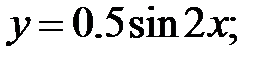 
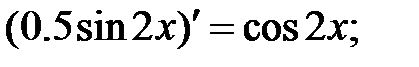
233.3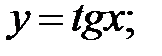 
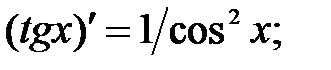233.4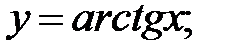 
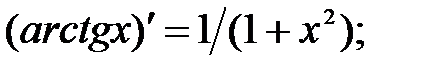
233.5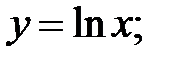 
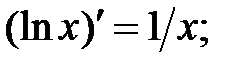233.6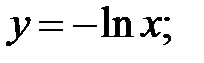 
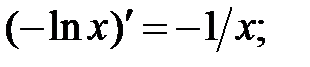
233.7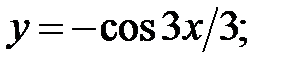 
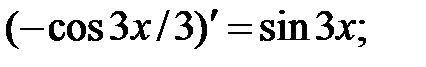
233.8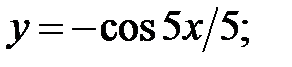 
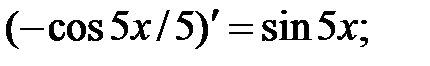233.9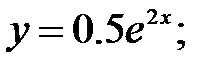 
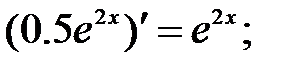
234. Вычислим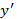 
и вместе с 
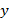подставим в данное уравнение.
234.1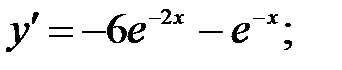 
; 
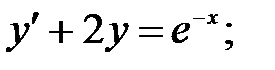
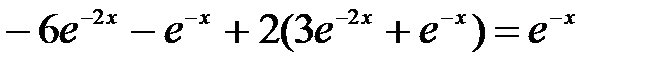234.2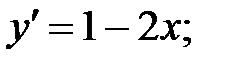 
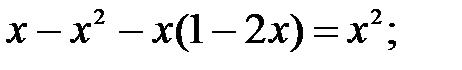
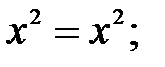
234.3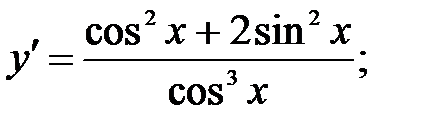 
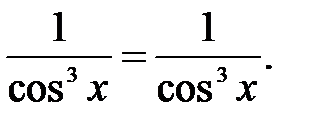
235.1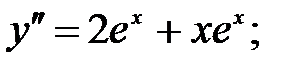 
235.2 
235.3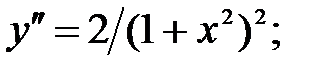 
235.4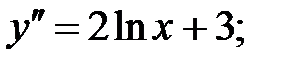 
235.5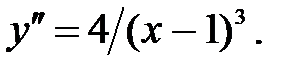 
236. Вычислим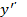 
и вместе с 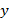подставим в данное уравнение.
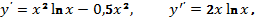
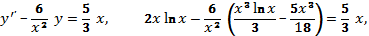
237.1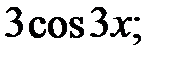 
237.2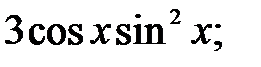 
237.3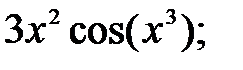 
237.4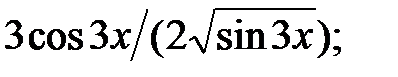 
237.5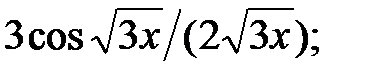 
237.6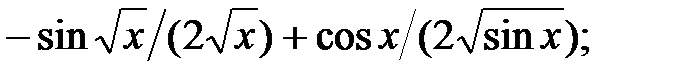 
237.7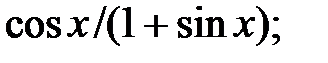 
237.8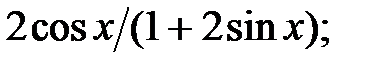 
237.9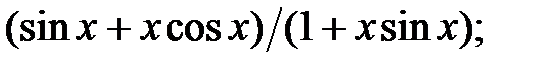 
237.10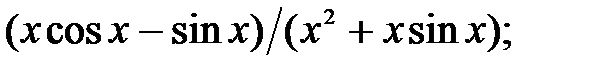 
237.11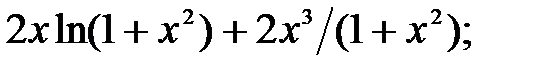 
237.12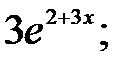 
237.13 
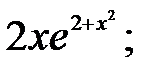237.14 
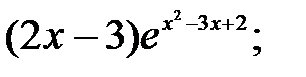237.15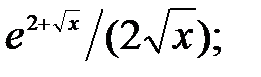 
237.16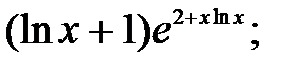 
237.17 
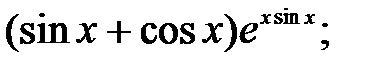237.18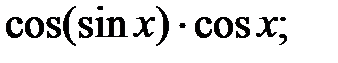 
237.19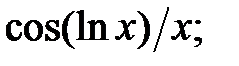 
237.20 
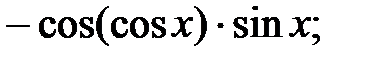237.21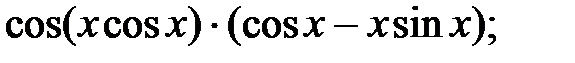 
237.22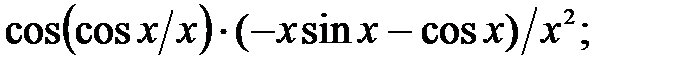 
237.23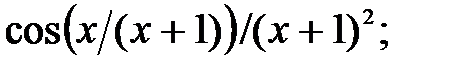 
237.24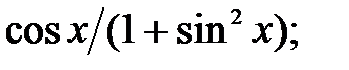 
237.25 
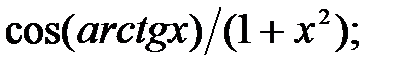237.26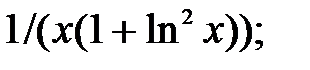 
237.27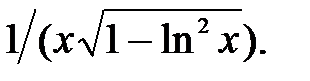 
238.1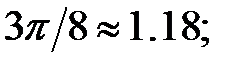 
238.2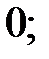 
238.3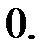 
239. 
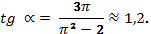
240. 1) Рассмотрим функцию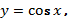 
обратная к ней: 
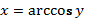. Пользуясь теоремой о производной обратной функции, имеем:
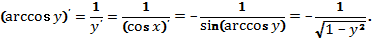
2) Рассмотрим функцию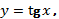 
обратная к ней: 
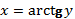. Пользуясь теоремой о производной обратной функции, имеем:
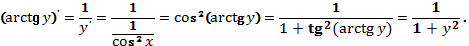
241.1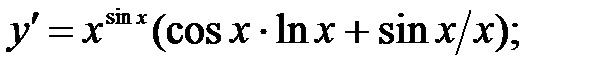 
241.2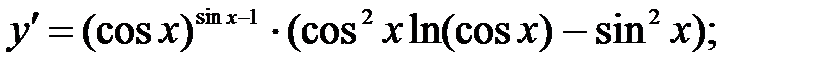 
241.3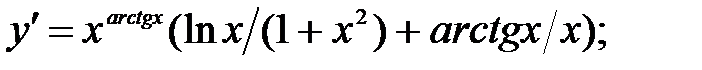 
241.4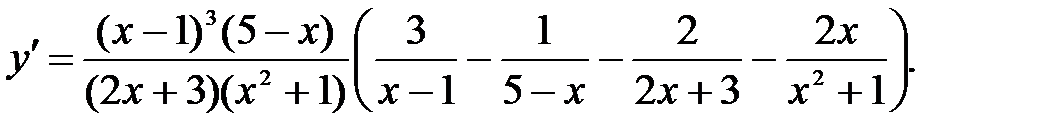 
242. 1) Преобразуем параметрическую форму записи, исключив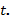 
Для этого возведем в квадрат 
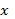и 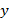, разделим первое уравнение на 4, а второе на 9 и сложим их:
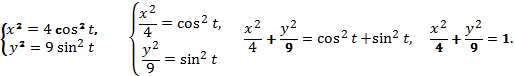
2)
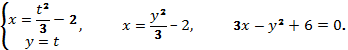
3)
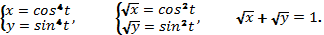
243.1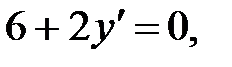 
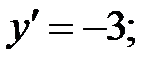243.2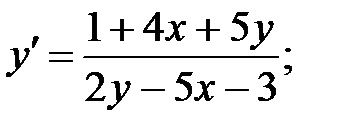 
243.3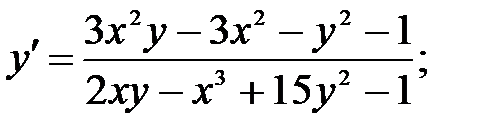 
243.4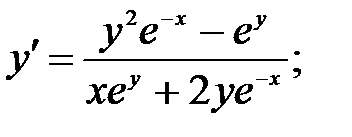 
243.5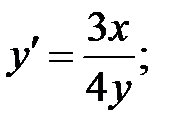 
243.6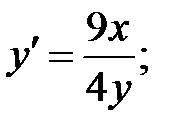 
243.7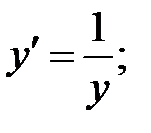 
243.8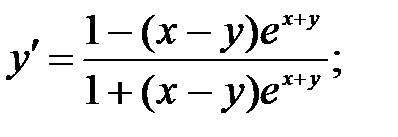 
243.9 
244.1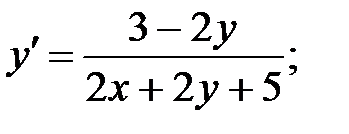 
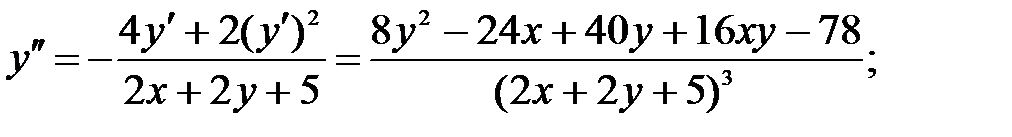
244.2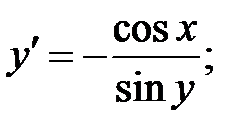 
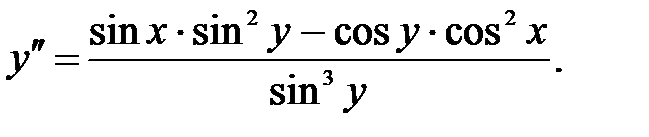
245. 
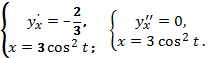
246.1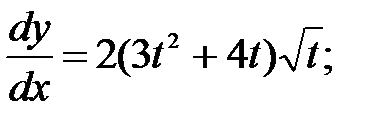 
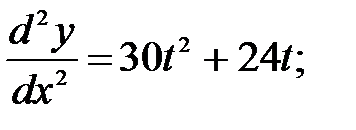246.2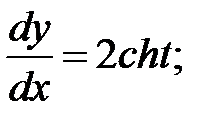 
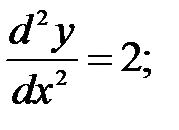
246.3 246.4.
247.1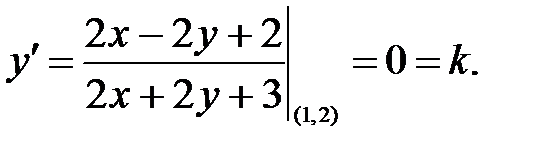 
Угловой коэффициент равен нулю, значит, уравнение касательной имеет вид: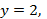 
а нормали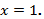 
247.2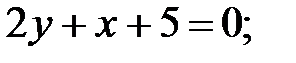 
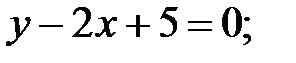247.3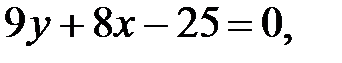 
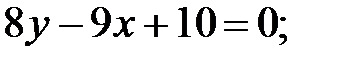
247.4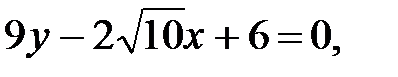 
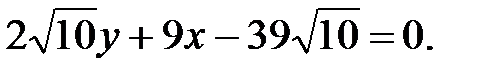
248.1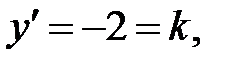 
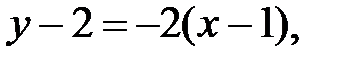
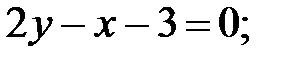
248.2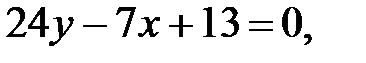 
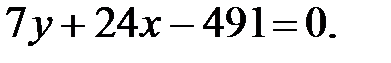
249.1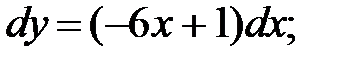 
249.2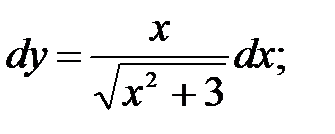 
249.3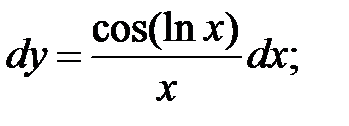 
249.4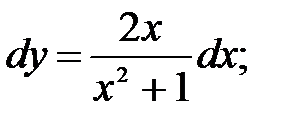 
249.5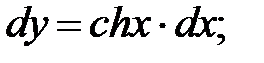 
249.6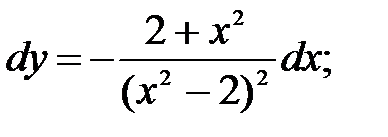 
249.7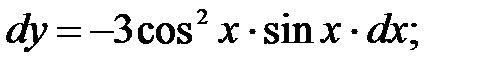 
249.8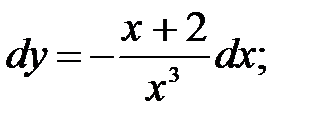 
249.9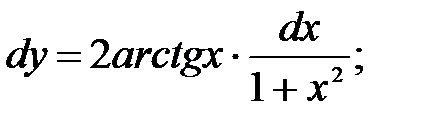 
249.10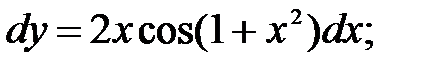 
249.11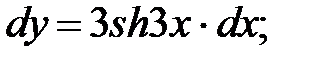 
249.12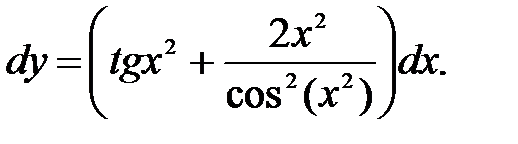 
250. 
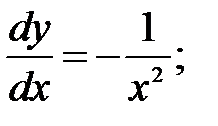С другой стороны 
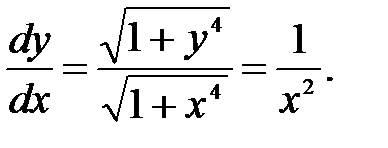Следовательно, равенство неверно.
251.1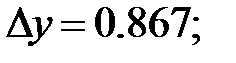 
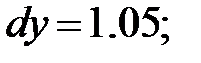251.2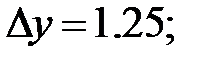 
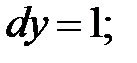
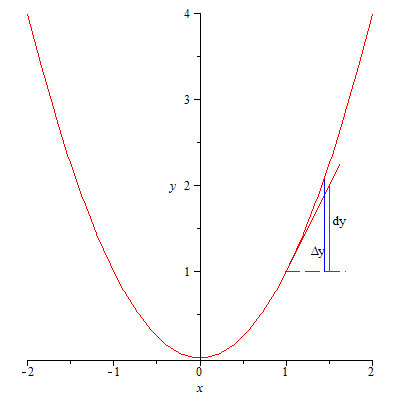
251.3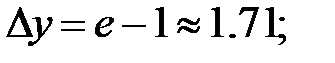 
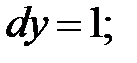251.4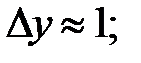 
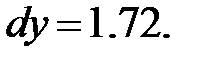
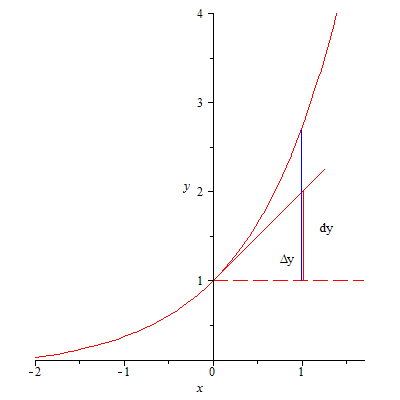
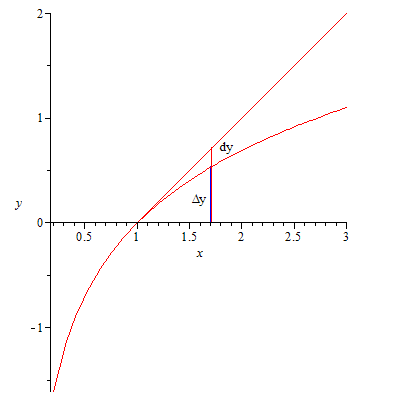
252.1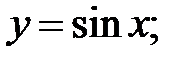 
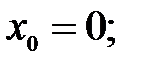
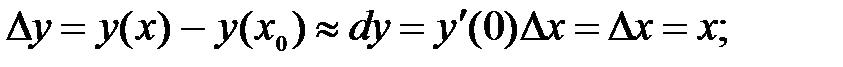
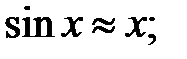
252.2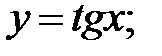 
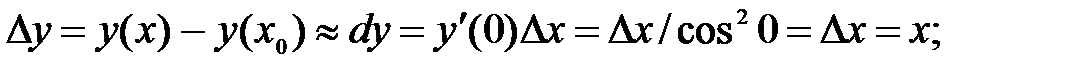
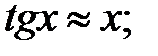
252.3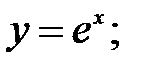 
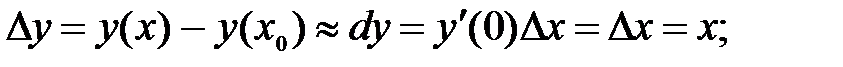
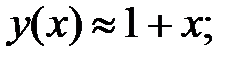
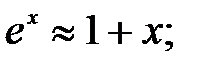
252.4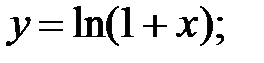 
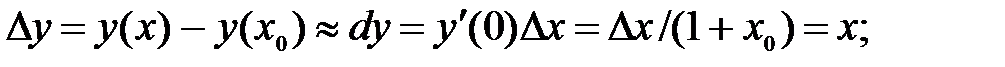
252.5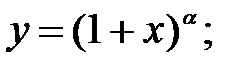 
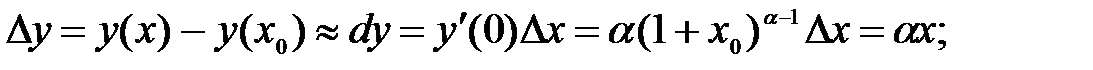
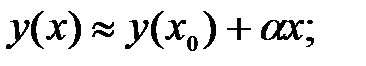
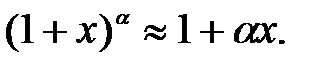
253. 
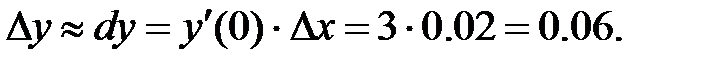
254. 
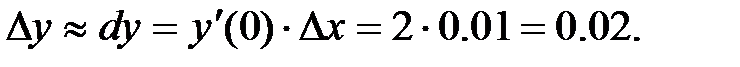
255.1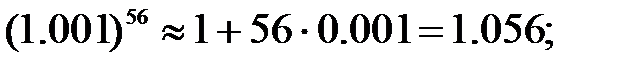 
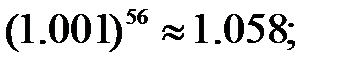
255.2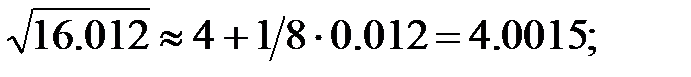 
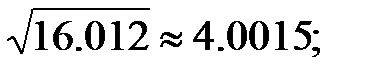
255.3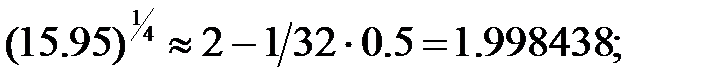 
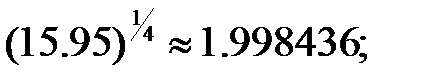
255.4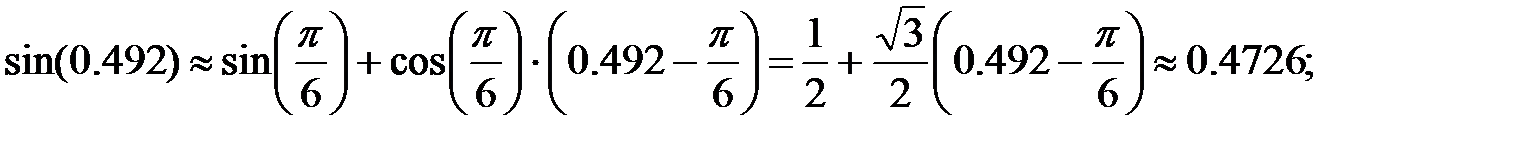 
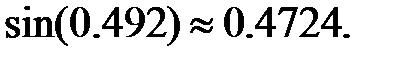
256.1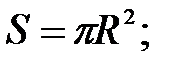 
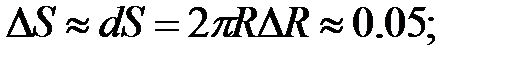256.2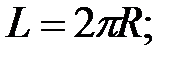 
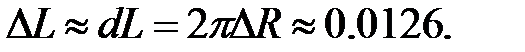
257. 
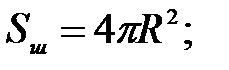
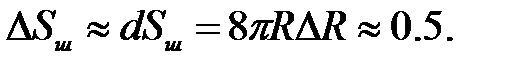
258. 
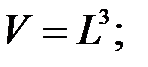
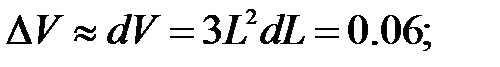
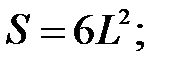
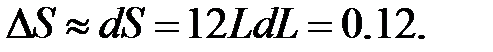
259.1 Существует число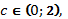 
такое что 
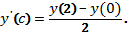Найдем это число.
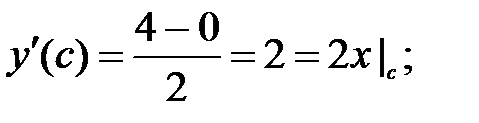
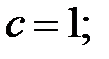259.2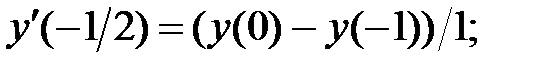 
259.3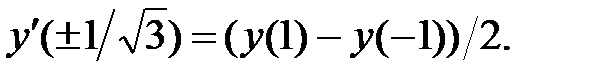 
260. 1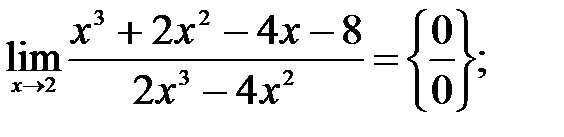 
По правилу Лопиталя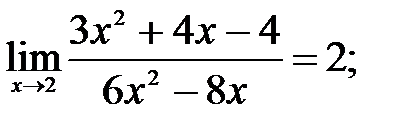 
260.2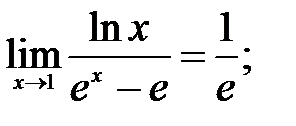 
260.3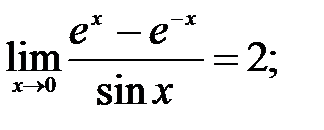 
260.4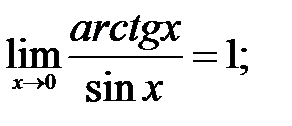 
260.5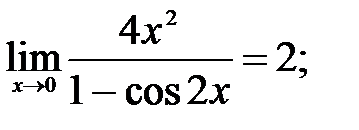 
260.6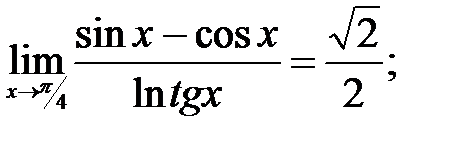 
260.7 0; 260.8 0.5; 260.9 1.
261. 1) 0;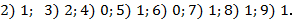 
262. 1) Прямая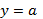 
является горизонтальной асимптотой, если 
.
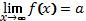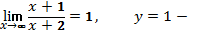горизонтальная асимптота.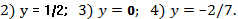 
263. 1) Если предел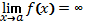 
, то прямая 
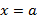является вертикальной асимптотой. 
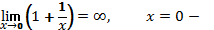вертикальная асимптота.
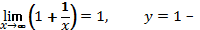горизонтальная асимптота.
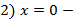вертикальная асимптота, 
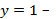горизонтальная асимптота.
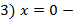вертикальная асимптота, 
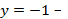горизонтальная асимптота.
264. 
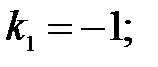
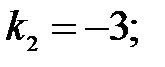
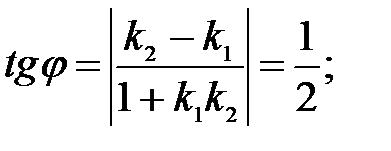
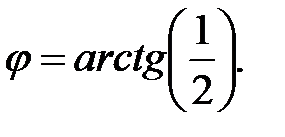265. 
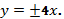
266. 
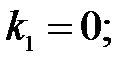
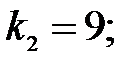
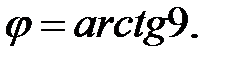267. 
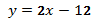. 268.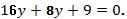 
269. 
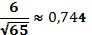. 270. 
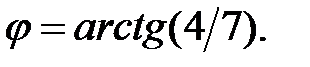271.1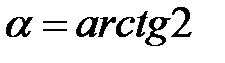 
в точке (0;0),
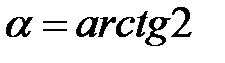в точке 
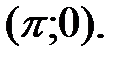271.2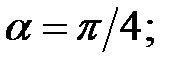 
в точке (0;0), 
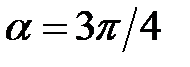в точке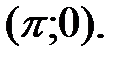
272. 
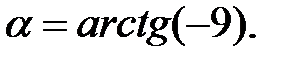273. 
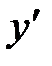убывает. 274. 
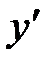возрастает.
275.1 275.2 275.3
