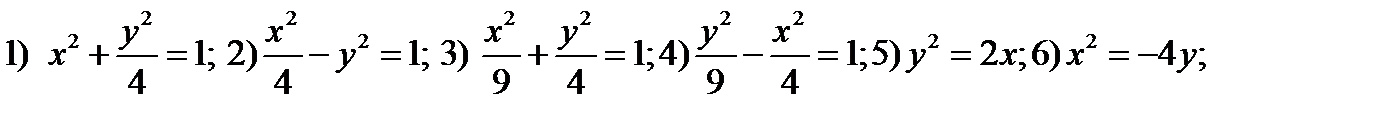40. Написать уравнение горизонтальной прямой линии проходящей через точку 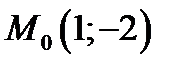 .
.
41. Написать уравнение вертикальной прямой проходящей через точку 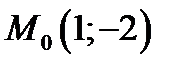 .
.
42. Написать уравнения прямой линии:
1) проходящей через точку 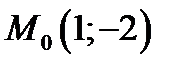 и имеющей угловой коэффициент
и имеющей угловой коэффициент  ;
;
2) проходящей через точку  и имеющей угловой коэффициент
и имеющей угловой коэффициент 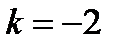 ;
;
3) проходящей через точку  параллельно оси ОХ;
параллельно оси ОХ;
4) проходящей через точку  параллельно оси ОУ;
параллельно оси ОУ;
5) проходящей через точки  ;
;
6) переписать уравнение прямой линии  в общем виде;
в общем виде;
7) переписать общее уравнение прямой линии  в виде уравнения
в виде уравнения
с угловым коэффициентом.
43. На прямой линии  найти точки: 1) у которой абсцисса
найти точки: 1) у которой абсцисса  ; 2) у которой ордината
; 2) у которой ордината 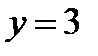 ; 3) Лежат ли точки
; 3) Лежат ли точки  на прямой
на прямой  .
.
44. Написать уравнение прямой линии проходящей через точку  параллельно
параллельно
прямой линии

45. Написать уравнение прямой линии проходящей через точку  и
и
перпендикулярно прямой линии:
1)  2)
2)  3)
3)  4)
4) 
46. Дать эскизы графиков прямых

47. Используя калькулятор вычислить угол наклона прямых линий

48. Найти точки пересечения прямой линии 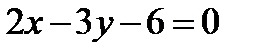 с осями ОХ, ОУ.
с осями ОХ, ОУ.
49. Найти точки пересечения прямых линий. Сделать чертёж.
1)  ;
;
2) 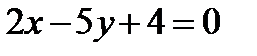 ,
, 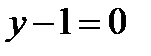 ;
;
3) 
50. НАЙТИ КООРДИНАТЫ ВЕРШИН ТРЕУГОЛЬНИКА  СО СТОРОНАМИ ОПРЕДЕЛЯЕМЫМИ УРАВНЕНИЯМИ
СО СТОРОНАМИ ОПРЕДЕЛЯЕМЫМИ УРАВНЕНИЯМИ

51. Найти уравнения прямых, на которых лежат стороны  , имеющего вершины
, имеющего вершины
 .
.
52. Найти острый угол между прямыми линиями:

53. Определить какие из точек 
лежат выше прямой, на прямой и ниже прямой, проходящей через точки  .
.
Напомним, что если точка лежит на прямой линии, то координаты точки являются решением уравнения прямой.
54. Даны уравнения сторон четырёхугольника 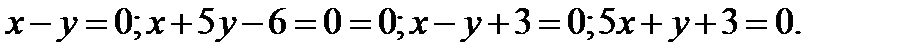 Найти уравнения его диагоналей.
Найти уравнения его диагоналей.
55. Найти абсциссу  , чтобы четырёхугольник с вершинами
, чтобы четырёхугольник с вершинами 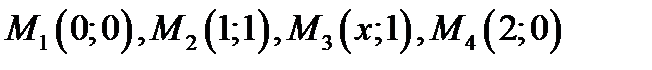 был параллелограммом.
был параллелограммом.
56. Доказать, что диагонали четырёхугольника с вершинами  взаимно перпендикулярны.
взаимно перпендикулярны.
57. Используя калькулятор вычислить расстояние от начала координат до прямой  .
.
58. Используя калькулятор вычислить расстояние от точки  до прямой
до прямой  .
.
59. Даны вершины  :
:  .Найти: 1) уравнение стороны
.Найти: 1) уравнение стороны 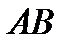 ; 2) уравнение высоты
; 2) уравнение высоты  ; 3) уравнение медианы
; 3) уравнение медианы  ; 4)точку пересечения высоты
; 4)точку пересечения высоты  и медианы
и медианы  ; 5) уравнение прямой, проходящей через вершину
; 5) уравнение прямой, проходящей через вершину  параллельно стороне
параллельно стороне  ; 6) длину высоты
; 6) длину высоты  ; 7) величины углов
; 7) величины углов  .
.
60. Найти точку 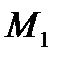 симметричную точке
симметричную точке  относительно прямой
относительно прямой 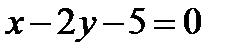 .
.
Кривые второго порядка
Парабола.
61. Написать уравнение параболы, вершина которой находится в начале координат, зная, что парабола расположена в правой полуплоскости симметрично относительно оси ОХ и её параметр равен 3.
62. Определить величину параметра и дать эскизы парабол

63. Определить величину параметра, фокус, директрису и дать эскиз.
1)  2)
2)  3)
3)  4)
4) 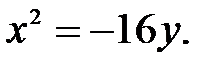
64. Написать уравнение параболы, которая имеет фокус  и вершину в начале координат.
и вершину в начале координат.
65. Написать уравнение параболы, которая имеет фокус  и вершину в начале координат.
и вершину в начале координат.
66. Написать уравнение параболы, у которой фокус  и уравнение директрисы
и уравнение директрисы 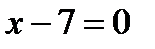 .
.
67. Написать уравнение параболы с вершиной  и осью симметрии
и осью симметрии  . Парабола проходит через точку
. Парабола проходит через точку
1) 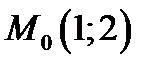 ; 2)
; 2)  .
.
68. Написать уравнение параболы с вершиной  и осью симметрии
и осью симметрии  . Парабола проходит через точку
. Парабола проходит через точку
1) 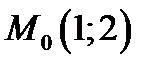 ; 2)
; 2)  .
.
69. Найти точки пересечения прямой и параболы:
1) 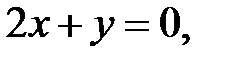
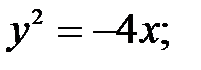 2)
2) 

Окружность
70.Написать уравнение окружности, зная
1) её центр О  и радиус
и радиус  ; 2) её центр О
; 2) её центр О 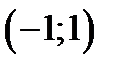 и радиус
и радиус  ;
;
71. Найти точки пересечения окружности 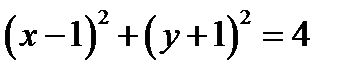 с осями координат.
с осями координат.
Эллипс.
72.Написать канонические уравнение эллипса, фокусы которого лежат на оси
абсцисс симметрично относительно начала координат, зная, что
1) его полуоси равны  ;
;
2) его большая полуось равна 5, а расстояние между фокусами  ;
;
3) расстояние между его фокусами  , а эксцентриситет
, а эксцентриситет  ;
;
4) расстояние между его директрисами равно 5 и расстояние между
фокусами  .
.
73.Написать канонические уравнение эллипса, фокусы которого лежат на оси ординат симметрично относительно начала координат, зная, что
1) его полуоси равны  ;
;
2) его большая полуось равна 10, а расстояние между фокусами  ;
;
3) расстояние между его фокусами 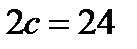 , а эксцентриситет
, а эксцентриситет  ;
;
4) расстояние между его директрисами равно  и расстояние между
и расстояние между
фокусами  ;
;
74. Дан эллипс  . Найти его
. Найти его
1) полуоси; 2) фокусы; 3) эксцентриситет; 4) уравнения директрис.
Дать эскиз.
75.Дать эскиз графикакривой и указать, что это за кривая
1)  ; 2)
; 2) 
76. Ординату каждой точки окружности с центром в начале координат и радиусом равным 1.
уменьшили в 3 раза. Назвать полученную кривую, определить её параметры и сделать
эскиз её графика.
77. Абсциссу каждой точки окружности с центром в начале координат и радиусом равным 1.
уменьшили в 2 раза. Назвать полученную кривую, определить её параметры и сделать
эскиз её графика.
78. Даны фокусы эллипса 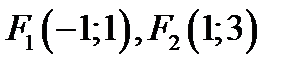 . Написать уравнения осей его симметрии.
. Написать уравнения осей его симметрии.
79. Даны: уравнение директрисы параболы  и её фокус
и её фокус  . Написать уравнения
. Написать уравнения
осей симметрии параболы.
Гипербола.
80.Написать уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, зная, что
1) её полуоси  ;
;
2) её горизонтальная ось 8, а расстояние между фокусами  ;
;
3) расстояние между её фокусами  , а эксцентриситет
, а эксцентриситет  ;
;
4) расстояние между её директрисами равно  и расстояние между
и расстояние между
фокусами 2с=26;
81. Написать уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, зная, что
1) её полуоси равны 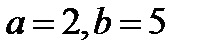 ;
;
2) её действительная полуось равна 4, а расстояние между фокусами  ;
;
3) расстояние между её фокусами  , а эксцентриситет
, а эксцентриситет  ;
;
4) расстояние между её директрисами равно  и расстояние между
и расстояние между
фокусами2с=26;
82. Дано уравнение гиперболы  . Найти её
. Найти её
1) полуоси; 2) фокусы; 3) эксцентриситет; 4) уравнения директрис; 5) уравнение асимптот.
83. Пусть задано уравнение кривой второго порядка:  . Если у кривой есть асимптоты, то написать их уравнения. Определить:
. Если у кривой есть асимптоты, то написать их уравнения. Определить: 
84. Пусть задано уравнение кривой второго порядка:  . Если у кривой есть асимптоты, то написать их уравнения. Определить:
. Если у кривой есть асимптоты, то написать их уравнения. Определить: 
85. Пусть задано уравнение кривой второго порядка:  . Если у кривой есть асимптоты, то написать их уравнения. Определить:
. Если у кривой есть асимптоты, то написать их уравнения. Определить: 
86.Определить тип кривой и дать эскиз её графика:

87. Определить, на какой из координатных осей лежат фокусы данных кривых второго
порядка