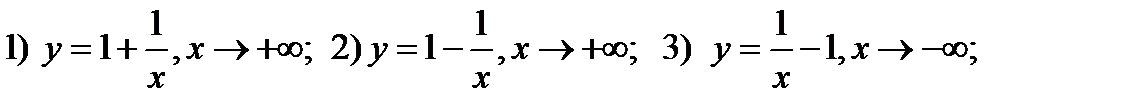237. Применив цепное правило вычислить производные функций
;
;
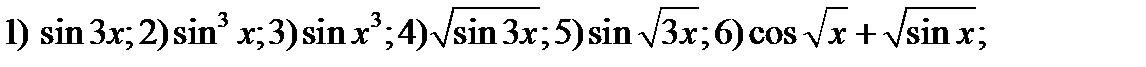
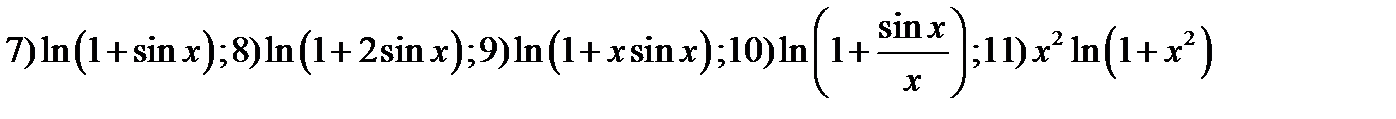23) 
238. Используя калькулятор, вычислить производные функций в заданной точке
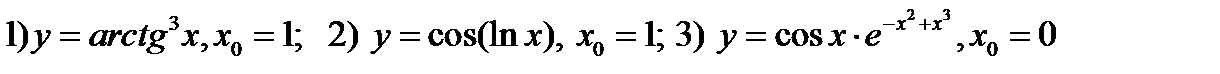
239. Вычислить угол между касательными к функции 
, проведёнными в
точках: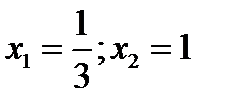 
240. Используя равенства
доказать формулы 
Логарифмическое дифференцирование
241. Вычислить производные заданных функций
Формулы неявного дифференцирования
242. Доказать, что данные формулы задают одну и туже кривую линию
243. Применяя правило неявного дифференцирования, вычислить
производные от функций заданных неявно (уравнениями)
244. Найти вторую производную функции 
заданной
неявно (уравнениями)
;
Формулы параметрического дифференцирования
245. Вычислить и записать в параметрическом виде производные 
от
функции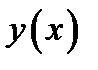 
заданной в параметрическом виде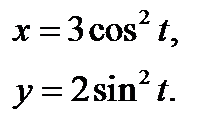 
246. Вычислить и записать в параметрическом виде первую и вторую производные
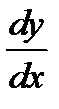и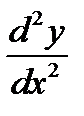 
от функций 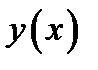заданных в параметрическом виде
4) 
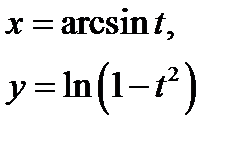
247. Написать уравнение касательной и нормали к кривым заданным
неявно (уравнениями) в точке 
248. Написать уравнение касательной и нормали к кривым заданным
параметрическими уравнениями
Дифференциал функции
249. Используя таблицу найти дифференциалы следующих функций 
250. Вычислить дифференциал дуги графиков функций
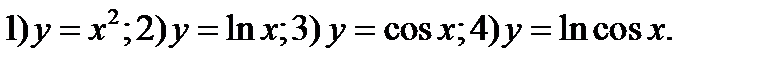
251. Изобразить геометрически приращение функции и дифференциал функции
при заданных величинах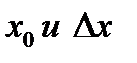 
. Оценить погрешность по графику
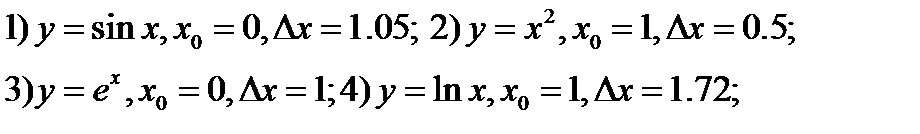
252. Используя понятие дифференциала получите приближённые формулы,
справедливые для малых 
253. Используя формулу линейного приближения функции, оценить максимальную погрешность при вычислении значения выражения 
, при 
,если аргумент 
задан приближённо 
.
254. Используя формулу линейного приближения функции, оценить максимальную
погрешность при вычислении значения выражения 
, при 
,если
аргумент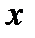 
задан приближённо 
.
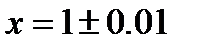255. Вычислить значение данного выражения двумя способами: а) используя
калькулятор и в) используя формулу линейного приближения функции
1) 
(взять 
) 3)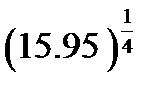 
(взять 
)
2) 
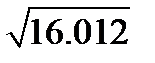(взять 
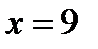); 4)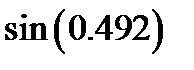 
(взять 
; 
;
).
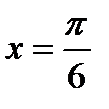256. Приближенно измеренный радиус круга оказался равны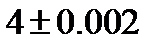м 
м.
Используя формулу линейного приближения, оценить какова будет максимальная ошибка при вычислении
1) площади круга, 2) длины окружности.
257. Приближенно измеренный радиус шара оказался равным 1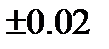 
м.
используя формулу линейного приближения, оценить какова будет
максимальная ошибка при вычислении площади поверхности (
)
этого шара. Для расчётов взять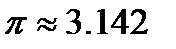 
.
258. Приближенно измеренное ребро куба оказался равным 
м. Используя
формулу линейного приближения, оценить какова будет максимальная ошибка при
вычислении объёма куба и площади поверхности куба.
Правило Лопиталя
259. Написать формулу Лагранжа (о среднем в дифференцировании) для функций
260. Используя правило Лопиталя, вычислить указанные пределы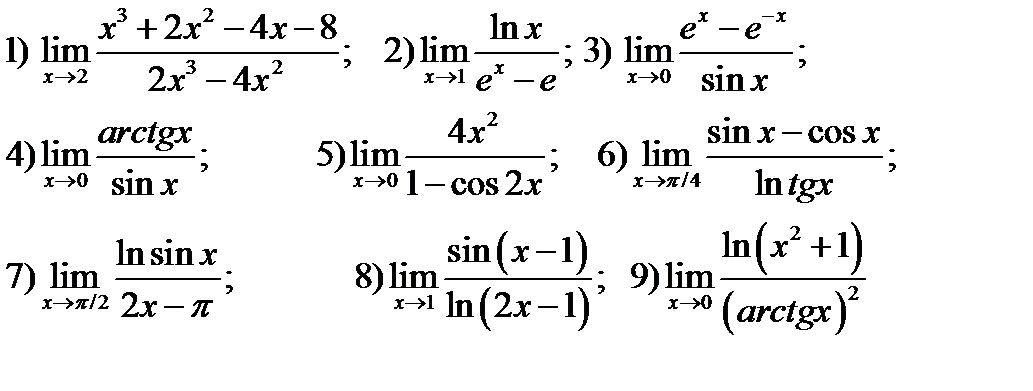 
261.Используя правило Лопиталя, вычислить указанные пределы
262. Написать уравнения горизонтальных асимптот
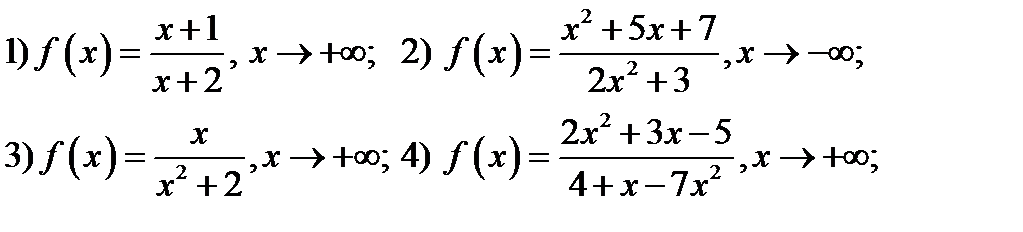
263. Написать уравнения горизонтальных и вертикальных асимптот и дать эскиз
графика функции
