40. 
41. 
42.1 
42.2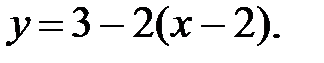 
42.3 
42.4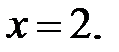 
42.5 
42.6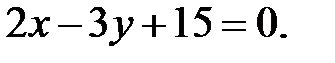 
42.7 
43.1 
43.2 
43.3 Обе точки принадлежат прямой.
44.1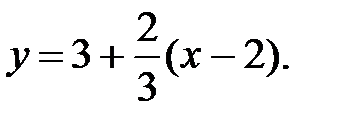 
44.2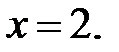 
44.3 
44.4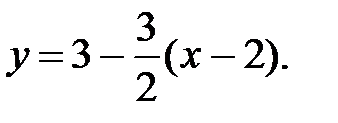 
44.5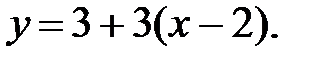 
44.6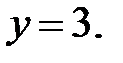 
44.7 
44.8 
45.1 
45.2 
45.3 
45.4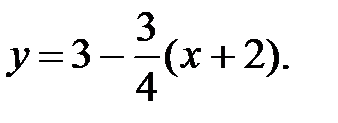 
46.1 46.2
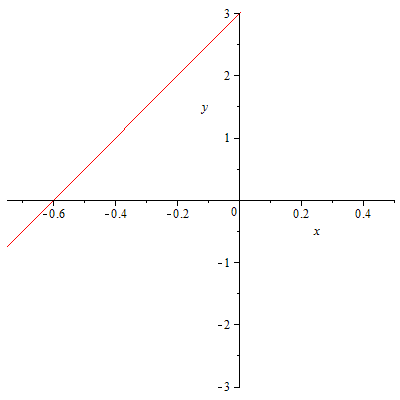
46.3 46.4
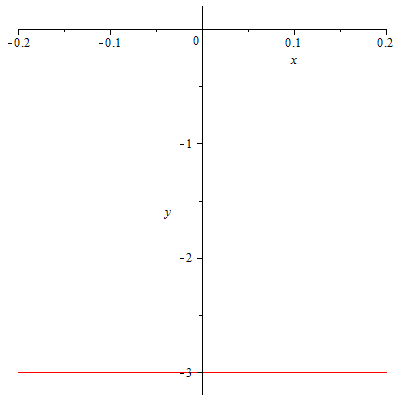
46.5
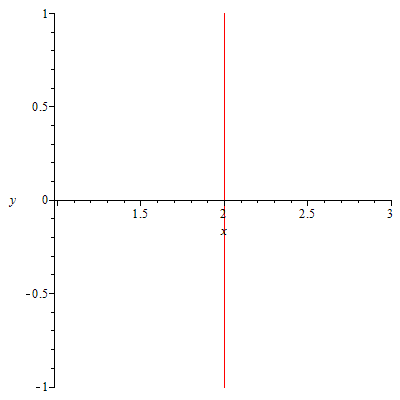
47.1 
47.2 
47.3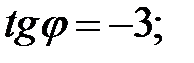 
47.4 
48. 
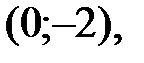
49.1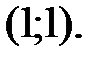 
49.2 (0.5; 1).
49.3 (2; 2). 50. 
51. 
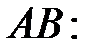
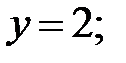
52.1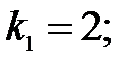 
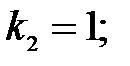
52.2 
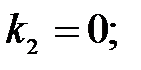
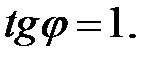
52.3 
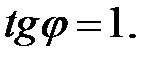
53. 
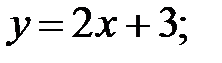А1 – выше; А2 – на прямой;
А3 – ниже; А4 – выше; А5 – ниже;
А6 – на прямой.
54. 
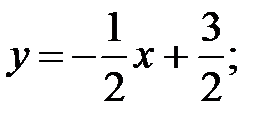
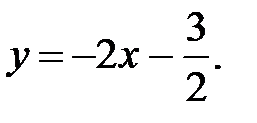
55. 
56 
57 
58. 
59.1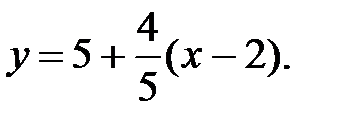 
59.2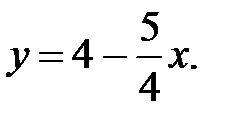 
59.3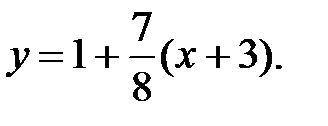 
59.4 
59.5 
59.6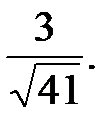 
59.7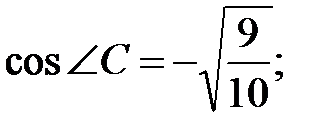 
60. 
-точка пересечения перпендикуляра, проходящего через точку М, с заданной прямой.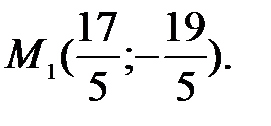 
Кривые второго порядка.
Парабола.
61. 
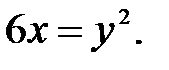
62.1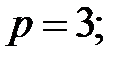 
62.2 
62.3 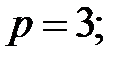62.4 
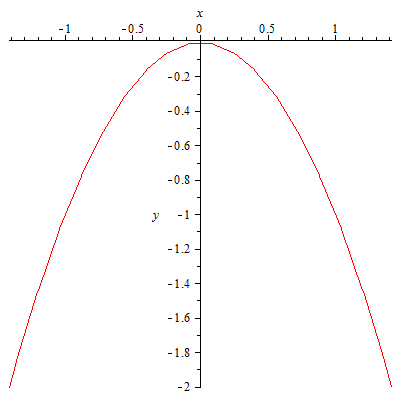
63.1 
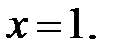63.2 
63.3 
63.4 
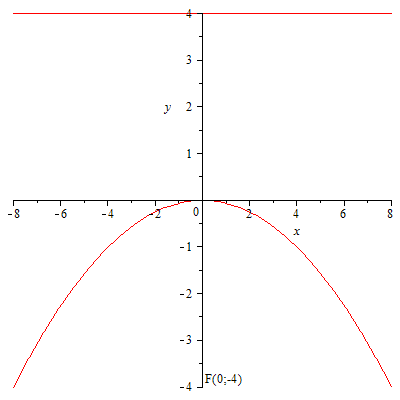
64. 
65. 
66. 
. 67.1 
67.2 
68.1 
68.2 
69.1 
69.2 Точек нет.
Окружность.
70.1 
70.2 
71. 
Эллипс.
72.1 
72.2 
72.3 
72.4 
73.1 
73.2 
73.3 
73.4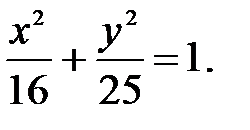 
74. 
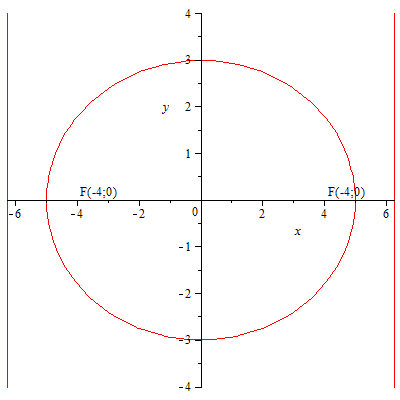
75.1 75.2
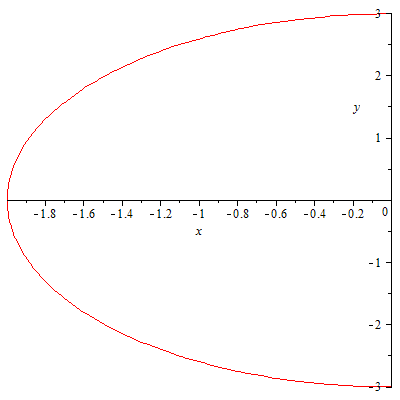
76. Эллипс. 
77. Эллипс 
78. 
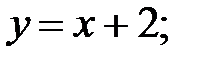
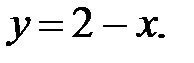79. 
Гипербола.
80.1 
80.2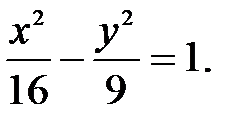 
80.3 
80.4 
81.1 
81.2 
81.3 
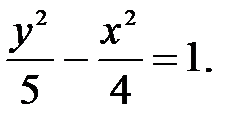81.4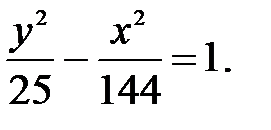 
82. 
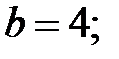
83. Эллипс. 
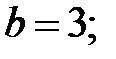
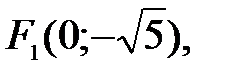84. Гипербола. 
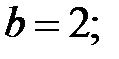
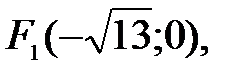
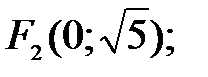
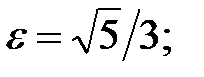
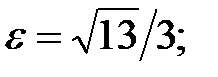
. асимптоты: 
85. Парабола. 
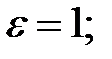директриса: 
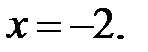86.1 Гипербола.
86.2 Гипербола 86.3 Гипербола
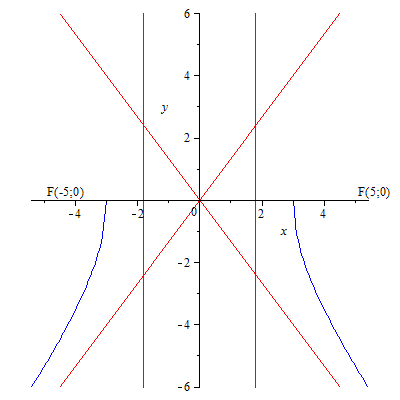
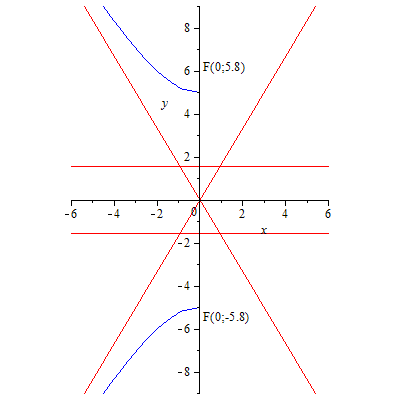
86.4 Гипербола.
87.1 На оси Оу. 87.2 На оси Ох. 87.3 На оси Ох. 87.4 На оси Оу. 87.5 На оси Ох. 87.6 На оси Оу.
Кривые в полярной системе координат
89.
90.1 х=2,у=0. 90.2 
90.3 
90.4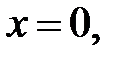 
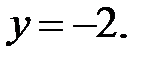90.5 
90.6 
90.7 
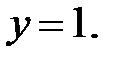90.8 
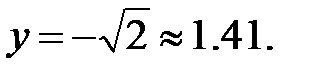
90.9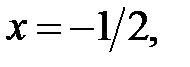 
90.10 
91 
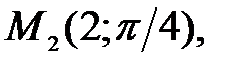
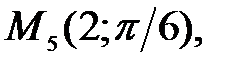
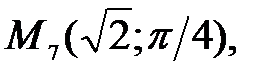
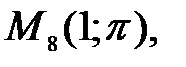
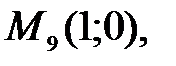
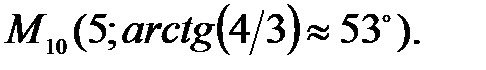
92.1 92.2
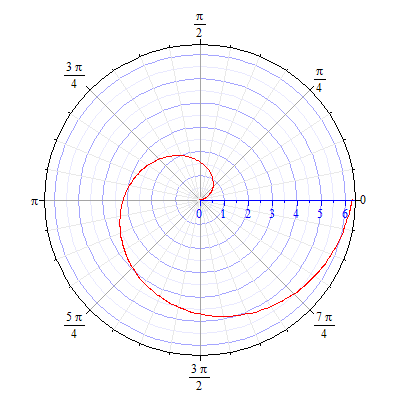
92.3 92.4
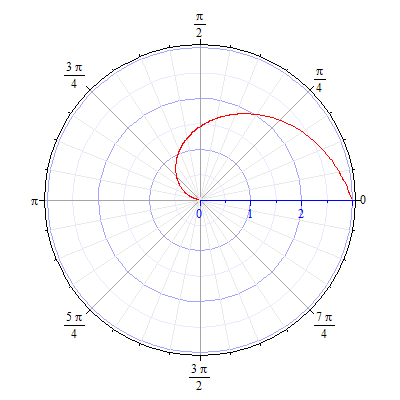
92.5 92.6
92.7 92.8
92.9
93.1 При замене 
, 
уравнение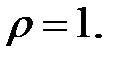 
93.2 1 При замене 
, 
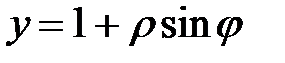уравнение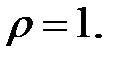
93.3 Парабола. 
Формулы перехода: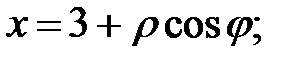 
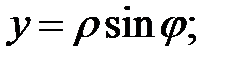полярная ось направлена вдоль оси Ох; полюс совпадает с фокусом. При подстановке в уравнение получаем 
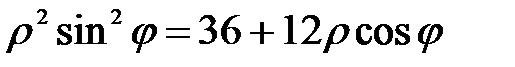или 
, или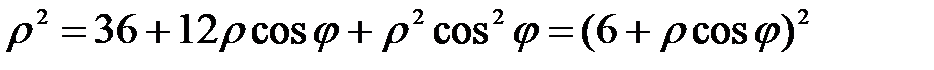 
. Разрешая это уравнение относительно 
получаем 
каноническое уравнение параболы в полярной системе координат.
93.4 Парабол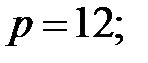а. 
Формулы перехода: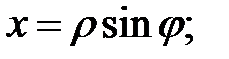 
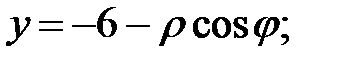полярная ось направлена вдоль оси Оу в противоположную сторону. При подстановке в уравнение получаем 
или 
или 
. Решая это уравнение относительно получим 
каноническое уравнение параболы в полярной системе координат.
93.5 Эллипс, вытянут вдоль оси Оу. 
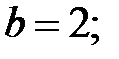
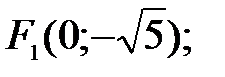
Формулы перехода: 
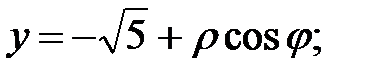
полярная ось направлена вдоль оси Оу и совпадает по направлению. Полюс в фокусе 
. При подстановке в уравнение получаем 
Приводим к общему знаменателю и освобождаемся от 
, получаем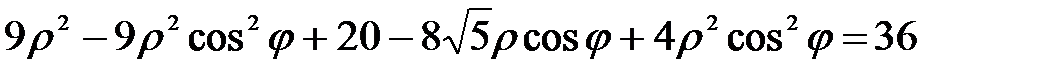 
или 
. Решая это уравнение относительно получим 
- каноническое уравнение эллипса в полярной системе координат. 93.6 Гипербола.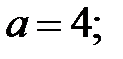 
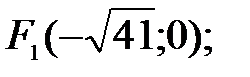
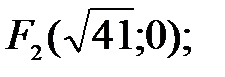Формулы перехода: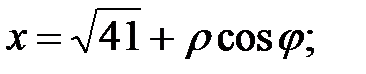 
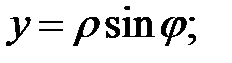полярная ось направлена вдоль оси Ох и совпадает с ней по направлению. При подстановке в уравнение получаем: 
Приводим к общемузнаменателюи освобождаемся от , получаем 
или 
. Решая это уравнение относительно получим 
-каноническое уравнение гиперболы в полярной системе координат.
94.1 
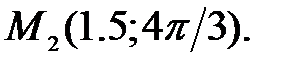94.2 
94.3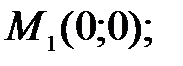 
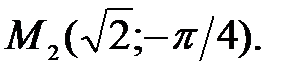94.4 
Элементы векторной алгебры.
95.1 
95.2 
95.3 
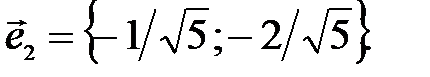
96.1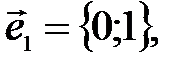 
96.2 
96.3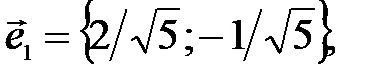 
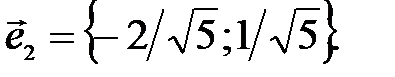98.1 
98.2 
98.3 
99. №1, №5, №6. 100.1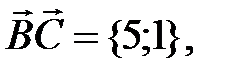 
100.2 
101. 
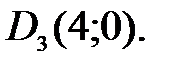102.1 
102.2 
102.3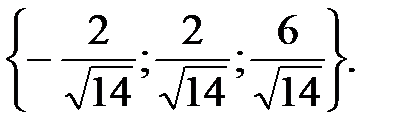 
103. Да, так как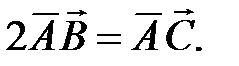 
104.1 
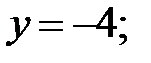
104.2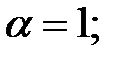 
105.1 
105.2 
105.3 
105.4 4; 105.5 3; 105.6 2; 105.7 
106. 
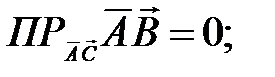
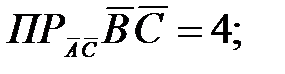
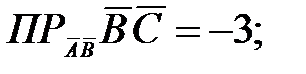
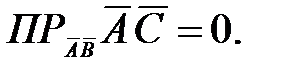107 
108. 
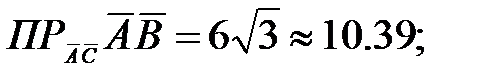
109. 
110. 
111. 
112. 
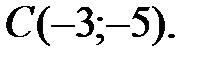
113.1 
113.2 
113.3 
113.4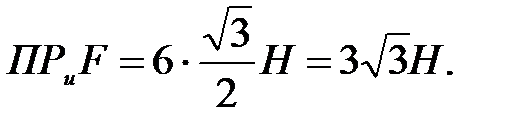 
114.1 
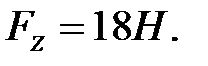114.2 
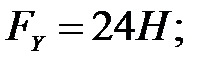
114.3 
115. 
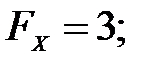
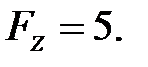
116.1 
116.2 
116.3 
116.4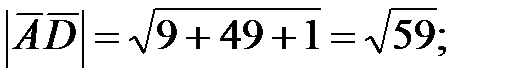 
117.1 0;
117.2 9; 117.3 20. 118. Вектор 
перпендикулярен векторам 
и 
. 119. 
120.1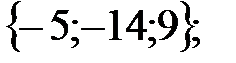 
120.2 
121.1 0; 121.2 
122.1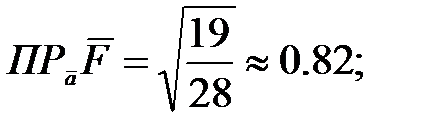 
122.2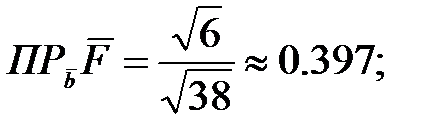 
122.3 
123. 
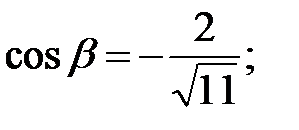
124. 0. 125.1 -4; 125.2 0.
Векторное произведение.
126.1 -50; 126.2 
126.3 
127.1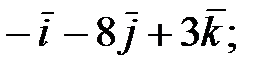 
127.2 
127.3 
127.4 
127.5 
128. 
129.1 
129.2 
130.1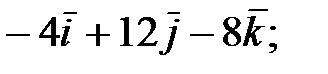 
130.2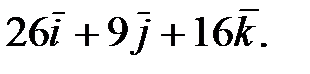 
131. 
132. 
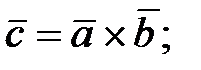См. 131. Все вектора - 
где 
произвольное число. 134.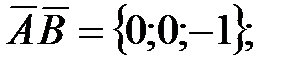 
135. 
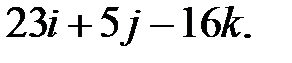
Смешанное произведение.
136. 
. 137.1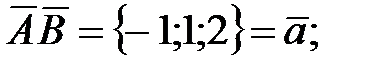 
137.2 
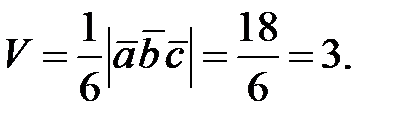138. Да, так как 
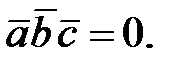139. Да.
Плоскости и прямые в пространстве.
140.1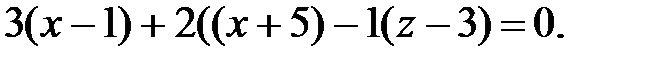 
140.2 
140.3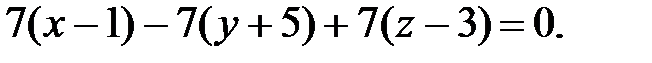 
140.4 
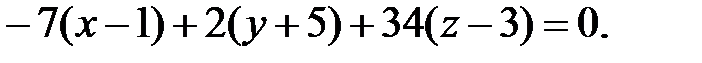141.1 
141.2.1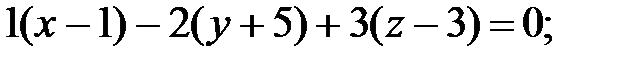 
141.2.2 
141.2.3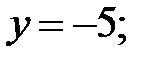 
141.2.4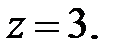 
141.3.1 141.3.2 141.3.3 141.4
141.5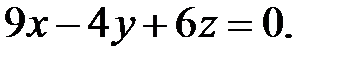 
142.1 Первая пара.
142.2 Первая и третья пары. 143. 
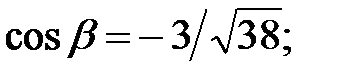
144.1 
144.2 
145.1 
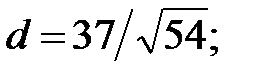145.2 
146. Уравнения перпендикуляра, проходящего через точку М0
Его параметрические уравнения: 
Находим точку пересечения перпендикуляра и плоскости: 
Тогда точка пересечения Р(-1;0;1). Она является серединой отрезка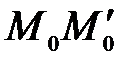 
. 
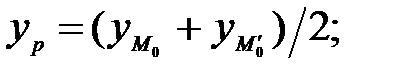
Отсюда находим координаты симметричной точки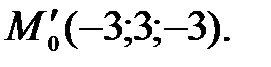 
147.1 
или 
147.2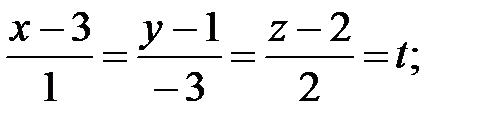 
или 
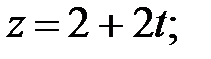
147.3 
или 
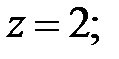
147.4 или
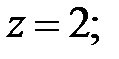
147.5 
или 
147.6 
или 
148.1 Для параллельности прямых необходимо выполнение коллинеарности направляющих векторов. 3 и 4 параллельны. 148.2 Прямые перпендикулярны, если скалярное произведение направляющих векторов равно нулю. 3 и 4 прямые перпендикулярны.
149.1 Направляющие вектора прямых: 
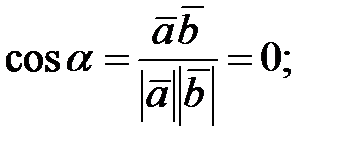
149.2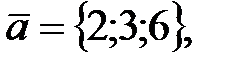 
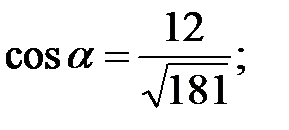149.3 
150.1 Необходимо найти точку, через которую проходит прямая и направляющий вектор. 
150.2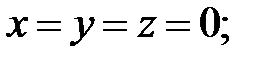 
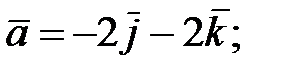
150.3 
150.4 
151.1 Направляющий вектор первой прямой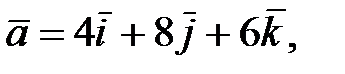 
второй прямой 
151.2 
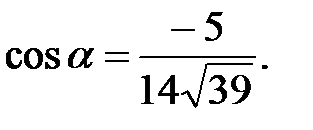152. Составим уравнение плоскости проходящей через точку М0
и перпендикулярно заданной прямой. В качестве нормального вектора к плоскости можно взять направляющий вектор прямой. Уравнение плоскости: 
или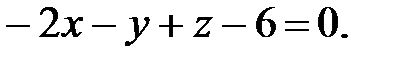 
Найдем точку пересечения плоскости и заданной прямой: 
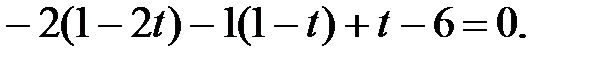Из этого уравнения следует, что пересечение происходит при 
Координаты точки пересечения 
Точка пересечения является серединой отрезка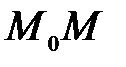 
. Из этого следует 
153. Возможны три случая 1) прямая и плоскость параллельны (уравнение плоскости после подстановки параметрических уравнений прямой неразрешимо относительно параметра); 2) прямая и плоскость пересекаются (уравнение плоскости после подстановки параметрических уравнений прямой разрешимо относительно параметра); 3) прямая принадлежит плоскости (уравнение плоскости после подстановки параметрических уравнений прямой выполняется при любом значении параметра). 153.1 Плоскость и прямая пересекаются: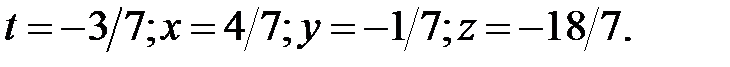 
153.2 Плоскость и прямая параллельны;
153.3 Прямая принадлежит плоскости; 153.4 Плоскость и прямая параллельны;
153.5 Плоскость и прямая пересекаются: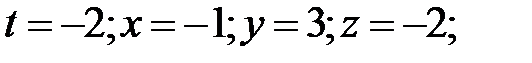 
153.6 Плоскость и прямая параллельны. 154. Вычисляем угол между направляющим вектором прямой и нормалью к плоскости; затем вычисляем синус требуемого угла. 154.1 
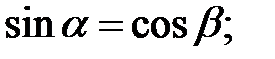
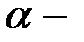угол между прямой и плоскостью. 154.2 
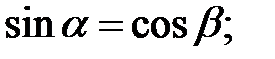
154.3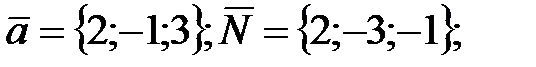 
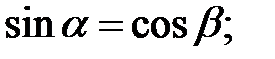155. 
156. С плоскостью х=0: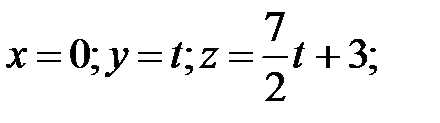 
С плоскостью у=0: 
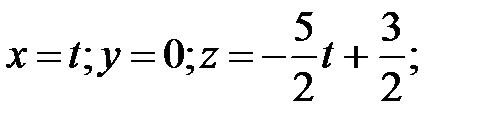С плоскостью z=0: 
