58 Найти радиус траектории протона в магнитном поле с индукцией В=1 Тл, если он движется перпендикулярно линиям индукции поля и обладает кинетической энергией W=1 МэВ.
59 Какова должна быть скорость электрона, чтобы его траектория была прямолинейной при движении во взаимно перпендикулярных магнитном и электрическом полях? Поля считать однородными с напряженностью Н=200 А/м и Е=1000 В/м соответственно.
60 На расстоянии d=3 мм параллельно прямолинейному длинному проводнику движется электрон с кинетической энергией Wк=200 эВ. Какая сила будет действовать на электрон, если по проводнику пропустить ток I=20 А?
61 Какова скорость движения автомобиля, если в его вертикальной антенне длиной L=1,5 м индуцируется ЭДС e=6×10-4 В? Горизонтальную составляющую магнитного поля Земли принять равной Н=16 А¤м. Считать, что автомобиль движется перпендикулярно магнитному меридиану.
62 Круглая рамка площадью S=50 см2, состоящая из N=100 витков, расположена в однородном магнитном поле с индукцией В=0,01 Тл перпендикулярно полю. В течение времени t=0,05 с рамку удалили за пределы поля. Рассчитать ЭДС индукции в рамке.
63 В однородном магнитном поле напряженностью Н=500 А/м равномерно вращается круглая рамка радиусом r=10 см2, имеющая N=50 витков. Ось вращения рамки совпадает с ее диаметром и перпендикулярна линиям индукции поля. Сопротивление рамки R=1 Ом, а угловая скорость ее вращения w=10 с‑1. Найти максимальную силу тока в рамке.
64 В соленоиде сила тока равномерно возрастает от I1=0 до I2=50 А в течение t=0,5 с, при этом соленоид накапливает энергию W=50 Дж. Какая ЭДС индуцируется в соленоиде?
65 Число витков соленоида без сердечника равно N=400, длина соленоида l=20 см, поперечное сечение S=4 см2, а сопротивление обмотки R=16 Ом. Сила тока в соленоиде возросла от I1=0 до I2=10 А. Какое количество электричества индуцировалось в соленоиде?
66 На 1 см однослойного соленоида без сердечника приходится N=40 витков. Объем соленоида V=800 см3. При какой скорости изменения силы тока в соленоиде индуцируется ЭДС самоиндукции e=0,5 В?
67 Виток радиусом r=1 см находится в магнитном поле напряженностью Н=20 кА/м. Плоскость витка перпендикулярна линиям индукции магнитного поля. Каково сопротивление R витка, если при уменьшении напряженности поля до нуля по нему протекает заряд q=1 мКл?
68 В однородном магнитном поле с индукцией В=0,01 Тл под углом б=450 к полю расположена медная квадратная рамка со стороной а=0,1 м. Диаметр провода d=0,2 мм. Рамку повернули перпендикулярно полю. Какое количество электричества индуцировалось в рамке?
69 На концах крыльев самолета размахом L=15 м, летящего со скоростью V=900 км/ч, возникает ЭДС индукции e=0,15 В. Определить вертикальную составляющую магнитного поля Земли.
70 Перпендикулярно линиям индукции однородного магнитного поля индукцией В=0,3 Тл движется проводник длиной L=30 см со скоростью V=10 м/с, перпендикулярной проводнику. Определить ЭДС, индуцируемую в проводнике.
71 Источник тока подключили к катушке сопротивлением R=40 Ом и индуктивностью L=0,4 Гн. Через какое время сила тока в цепи достигнет 90% от максимального значения?
72 Источник тока, подключенный к катушке индуктивностью L=1 Гн, отключили, не разрывая цепь. За время t=0,69 с сила тока в цепи уменьшилась в 1000 раз. Определить сопротивление катушки.
73 Через t=5 мс после размыкания цепи сила тока в ней уменьшилась в 5 раз. Найти индуктивность цепи, если ее сопротивление составляет R=46 Ом.
74 По цепи сопротивлением R=10 Ом и индуктивностью L=0,03 Гн течет ток I=40 А. Найти силу тока в цепи через t=0,5 мс после отключения источника.
75 Обмотка соленоида имеет сопротивление R=20 Ом. Какова его индуктивность, если при прохождении тока за t=0,02 с в нем выделяется количество теплоты, эквивалентное энергии магнитного поля соленоида?
76 Определить объемную плотность энергии магнитного поля соленоида без сердечника, если он намотан в один слой из провода диаметром d=0,1 мм и по нему течет ток I=0,2 А.
77 Найти силу тока, которую необходимо поддерживать в соленоиде, чтобы он создавал магнитный поток ФВ=2×10-4 Вб, если индуктивность соленоида L=0,3 Гн, а число витков в соленоиде 750.
78 По обмотке электромагнита сопротивлением R=10 Ом и индуктивностью L=2 Гн течет постоянный электрический ток силой I=2 А. Чему равна энергия магнитного поля электромагнита через t=0,1 с после отключения источника?
79 Круглая рамка радиусом r=2 см, по которой протекает ток I=1 А, находится в воздухе в однородном магнитном поле напряженностью Н=75 А/м. Плоскость рамки составляет угол b=300 с вектором напряженности поля. Какую работу необходимо совершить, чтобы повернуть рамку перпендикулярно полю?
80 Однородное магнитное поле действует с силой F=0,001 Н на 1 см длины прямого провода с током с силой I=50 А, расположенного перпендикулярно полю. Найти объемную плотность энергии поля.
2 ВОЛНОВАЯ ОПТИКА, КВАНТОВАЯ ПРИРОДА ИЗЛУЧЕНИЯ, ЭЛЕМЕНТЫ АТОМНОЙ ФИЗИКИ И КВАНТОВОЙ МЕХАНИКИ
Основные законы и формулы
Скорость света в среде
,
где с - скорость света в вакууме, м/с; n - показатель преломления среды.
Оптическая длина пути световой волны
,
где l - геометрическая длина пути световой волны в среде с показателем преломления n.
Зависимость разности фаз Δφ от оптической разности хода Δ световых волн
,
где l - длина световой волны, м.
Условие максимального усиления света при интерференции
, (k =0, 1, 2,...).
Условие максимального ослабления света при интерференции
, (k =0, 1, 2,...).
Оптическая разность хода световых волн, возникающая при отражении монохроматического света от тонкой пленки,
,
или
,
где d - толщина пленки, м; n - показатель преломления пленки; α - угол падения; β - угол преломления света в пленке.
Радиус светлых колец Ньютона в отраженном свете
, (k =1, 2, 3,.....),
где k - номер кольца; R - радиус кривизны, м.
Радиус внешней границы m -ой зоны Френеля для сферических волн:
,
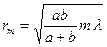где а и b – расстояние от источника до волнового фронта и от волнового фронта до рассматриваемой точки пространства, соответственно, м; m – номер зоны Френеля.
Радиус внешней границы m-ой зоны Френеля для плоских волн:
,
где b – расстояние от волнового фронта до рассматриваемой точки пространства, м; m – номер зоны Френеля.
Угол j отклонения лучей, соответствующий максимуму (светлая полоса) при дифракции на одной щели, определяется из условия
, (k =0, 1, 2, 3,....),
где a - ширина щели, м; k - порядковый номер максимума.
Угол j отклонения лучей, соответствующий максимуму (светлая полоса) при дифракции на дифракционной решетке, определяется из условия
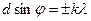, (k =0, 1, 2, 3,....),
где d - период дифракционной решетки, м.
Закон Брюстера
,
где eВ - угол падения, при котором отразившийся от диэлектрика луч полностью поляризован; n21 - относительный показатель преломления второй среды относительно первой.
Закон Малюса
,
где Io - интенсивность плоскополяризованного света, падающего на анализатор, Вт/м2; I - интенсивность этого света после анализатора, Вт/м2; a - угол между направлением колебаний электрического вектора света, падающего на анализатор, и плоскостью пропускания анализатора (если колебания электрического вектора падающего света совпадают с этой плоскостью, то анализатор пропускает данный свет без ослабления), град.
Угол поворота плоскости поляризации монохроматического света при прохождении через оптически активное вещество:
1) 
(в твердых телах),
где α – постоянная вращения, град/м; l – расстояние, проходимое светом в оптически активном веществе, м;
2) 
(в растворах),
где [ α ]– удельное вращения, (град∙м2)/кг; С – массовая концентрация оптически активного вещества в растворе, кг/м3.
Закон Стефана-Больцмана
Re=sT4,
где Re - энергетическая светимость (излучательность) абсолютно черного тела, Вт; s - постоянная Стефана-Больцмана, Вт/(м2∙К4); Т - термодинамическая температура Кельвина, К.
Закон смещения Вина
lm=b/T,
где lm - длина волны, на которую приходится максимум энергии излучения, м; b - постоянная Вина, м∙К.
Энергия фотона
, или 
,
где h - постоянная Планка, Дж∙с; 
- постоянная Планка, деленная на 2p, Дж∙с; n - частота фотона, с-1; w - циклическая частота, рад/с.
Масса фотона
m=e/c2=h/(cl) 
,
где с - скорость света в вакууме, м/с; l - длина волны фотона, м.
Импульс фотона
р ф =mc=h/l.
Давление р, производимое светом при нормальном падении на поверхность с коэффициентом отражения ρ
,
где Е – энергетическая освещенность поверхности численно равная энергии, падающей на единичную площадку в единицу времени, Дж/(м2∙с); w – объемная плотность энергии излучения, Дж/м3.
Формула Эйнштейна для фотоэффекта
hn=А+Тmax=A+mV2/2,
где hn - энергия фотона, падающего на поверхность металла, Дж; А - работа выхода электрона, Дж; Тmax - максимальная кинетическая энергия фотоэлектрона, Дж; m – масса электрона, кг; V – скорость электрона при вылете из металла, м/с.
Красная граница фотоэффекта
nо=А/h, или lо=hc/A,
где nо ‑ минимальная частота света, при которой еще возможен фотоэффект, с-1; lо ‑ максимальная длина волны при которой еще возможен фотоэффект, м; h - постоянная Планка, Дж∙с; с - скорость света в вакууме.
Длина волны де Бройля
l=h/p,
где р - импульс частицы, кг∙м/с.
Импульс частицы и его связь с кинетической энергией Т:
а) р=mov; 
(для нерелятивистского случая);
б) 
; 
(для релятивистского случая),
где mo - масса покоя частицы, кг; m - релятивистская масса, кг; v ‑ скорость частицы, м/с; с - скорость света в вакууме, м/с; Ео - энергия покоя частицы (Ео=moc2), Дж.
Соотношение неопределенностей Гейзенберга:
а) 
(для координаты и импульса),
где Dрх - неопределенность проекции импульса на ось Х; Dх - неопределенность координаты;
б) DЕDt ³ h (для энергии и времени),
где DЕ - неопределенность энергии, Дж; Dt - время жизни квантовой системы в данном энергетическом состоянии, с.
Массовое число ядра (число нуклонов в ядре)
А=Z+N,
где Z - зарядовое число (число протонов); N - число нейтронов.
Закон радиоактивного распада
, или 
,
где dN - число ядер, распадающихся за интервал времени dt; N - число ядер не распавшихся к моменту времени t; Nо - число ядер в начальный момент времени
(t = to); l - постоянная радиоактивного распада.
Число ядер, распавшихся за время t,
.
В случае, если интервал времени Dt, за который определяется число распавшихся ядер, много меньше периода полураспада Т1/2, то число распавшихся ядер можно определить по формуле
DN = lNDt.
Зависимость периода полураспада от постоянной радиоактивного распада
Т1/2=(ln 2)/l = 0,693/l.
Число N атомов, содержащихся в радиоактивном изотопе,
N = mNA/M,
где m - масса изотопа, М - молярная масса; NА - постоянная Авогадро.
Активность А радиоактивного изотопа
А = - dN/dt = lN, или А = lNoe-l t = Aoe-l t,
где dN - число ядер, распадающихся за интервал времени dt, Ао - активность изотопа в начальный момент времени.
Удельная активность изотопа
.
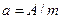Примеры решения задач
Пример 1. На мыльную пленку с показателем преломления n =1,33 падает белый свет под углом α =300. При какой наименьшей толщине d поверхность пленки, наблюдаемая в отраженном свете, будет окрашена в желтый свет? Считать длину волны желтого света равной λ =6∙10-7м.
Решение. Оптическая разность хода Δ световых волн, возникающая при отражении монохроматического света от тонкой пленки, в общем случае определяется по формуле
. (1)
Условие интерференционного максимума имеет вид
, (2)
где k =1, 2, 3 …‑ число длин полуволн, укладывающихся на оптической разности хода.
Приравняем правые части выражений (1) и (2):
. (3)
Из уравнения (3) находим искомую толщину пленки, учитывая, что наименьшая толщина будет соответствовать условию k =1:
.
Размерность формулы очевидна.
Проведем вычисления 
.
Ответ: 
.
Пример 2. Дифракционная решетка имеет N =100 штрихов на длине l =1 мм и расположена на расстоянии L =1 м от экрана. На решетку падает белый свет. Найти ширину ΔХ спектра первого порядка на экране, если длина волны красного цвета равна λ 1=720 нм, а фиолетового – λ 2=430 нм.
Рисунок 3 - Дифракция на дифракционной решетке
|
Решение. Схематически изобразим ход световых лучей при дифракции на дифракционной решетке (рис.3). Ширину спектра можно определить как разность расстояний Х2 между красной линией спектра первого порядка и центральным максимумом (белой полосой, соответствующей k =0) и расстоянием Х1 между фиолетовой полосой спектра того же порядка и центральным максимумом:
. (1)
Длины отрезков Х1 и Х2, как следует из рисунка 3, можно найти по формулам
, (2)
. (3)
Так, дифракционные углы, соответствующие спектру первого порядка, обычно малы, то можно считать, что 
. Воспользуемся условием максимума на дифракционной решетке:
, (4)
, (5)
где 
‑ период дифракционной решетки, а k – порядок спектра (по условию задачи k =1). Из (4) и (5) находим синусы углов дифракции:
, (6)
. (7)
Подставим выражения (6) и (7) в (2) и (3) соответственно:
, (8)
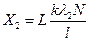. (9)
Путем подстановки (8) и (9) в (1) находим ширину спектра первого порядка:
.
Проверим размерность формулы:
.
Выполним вычисления: 
.
Ответ: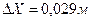 
.
Пример 3. На призму Николя падает естественный свет. Интенсивность света после прохождения через призму уменьшается на 55%. Определить коэффициент поглощения света в призме Николя.
 Рисунок 4 - Прохождение света через призму Николя
|
Решение. Рассмотрим прохождение естественного света через призму Николя (рис.4).
Естественный свет, падая на переднюю грань призмы Николя, вследствие явления двойного лучепреломления расщепляется на два луча: обыкновенный (о) и необыкновенный (е). Оба луча одинаковы по интенсивности и полностью поляризованы. Плоскость колебаний необыкновенного луча лежит в плоскости чертежа (плоскость главного сечения), а плоскость колебаний обыкновенного луча перпендикулярна плоскости чертежа. Обыкновенный луч испытывает полное отражение на границе АВ и попадает на нижнюю зачерненную грань призмы, где полностью поглощается. Необыкновенный луч проходит через призму, уменьшая интенсивность вследствие поглощения части света материалом призмы. Таким образом, интенсивность света, прошедшего через призму, может быть определена следующим образом:
, (1)
где I 0 и I – интенсивности света на входе и выходе из призмы Николя, k – коэффициент поглощения света. По условию задачи интенсивность света уменьшилась на 55%, следовательно, интенсивность света на выходе из призмы
. (2)
Подставляем (2) в (1) и находим
.
Ответ: k =0,1.
Пример 4. Абсолютно черная поверхность располагается перпендикулярно свету с длиной волны λ =0,5 мкм. При этом свет оказывает на поверхность давление равное р =10 мкПа. Определить число фотонов N, падающих на поверхность площадью S =1 см2 за время t =10 с.
Решение. Давление света определяется по формуле
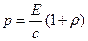, (1)
где 
‑ энергетическая освещенность, равная энергии, падающей на единичную площадку за единицу времени; ρ – коэффициент отражения, с= 3∙108 м/с – скорость света в вакууме. Так как поверхность абсолютно черная, то ρ =0. Согласно формуле Планка энергия одного фотона
, (2)
где h =6,625∙10-34Дж∙с – постоянная Планка, ν – частота света. С учетом (2) полная энергия светового потока
. (3)
Подставляя (3) в (1), получаем 
. Отсюда находим искомую величину 
.
Проверим размерность формулы 
.
Выполним расчеты: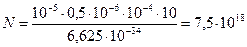 
.
Ответ: N =7,5∙1018.
Пример 5. Длина волны, на которую приходится максимум энергии в спектре излучения чёрного тела, l0=0,58 мкм. Определить энергетическую светимость (излучательность) Re поверхности тела.
Решение. Энергетическая светимость Rе абсолютно чёрного тела в соответствии с законом Стефана-Больцмана пропорциональна четвёртой степени термодинамической температуры и выражается формулой
, (1)
где s - постоянная Стефана-Больцмана; Т - термодинамическая температура.
Температуру Т можно вычислить с помощью закона смещения Вина:
, (2)
где b - постоянная закона смещения Вина.
Используя формулы (1) и (2), получаем
. (3)
Произведём вычисления:
.
Ответ: 
.
Пример 6. Металлическую пластинку освещают рентгеновским излучением с длиной волны λ =20 нм. Красная граница фотоэффекта для пластинки составляет λ 0=200 нм. Вблизи пластинки приложено задерживающее однородное электростатическое поле напряженностью Е =500 В/м. Определить максимальную длину пробега фотоэлектронов в этом поле.
Решение. Воспользуемся уравнением Эйнштейна для внешнего фотоэффекта
, (1)
где h =6,625∙10-34Дж∙с – постоянная Планка, с =3∙108 м/с – скорость света в вакууме, 
– работа выхода электронов из металла, m – масса электрона, V – скорость электрона при вылете из металла.
Фотоэлектроны задерживаются электростатическим полем (Ек2 =0), следовательно, работа поля, равная изменению кинетической энергии фотоэлектронов, может быть определена как
. (2)
С другой стороны, работа электростатического поля находится по формуле
, (3)
где l – расстояние проходимое электронами в электрическом поле, qе =‑1,6∙10‑19 Кл– заряд электрона. Приравнивая правые части выражений (2) и (3) с учетом знака заряда электрона, получаем
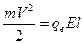. (4)
С учетом Авых и (4) уравнение (1) принимает вид
. (5)
Решая (5), находим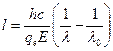 
.
Проверим размерность формулы 
.
Проведем расчеты 
.
Ответ: l =0,011 м.
Пример 7.Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов Δφ =51 В. Найти длину волны де Бройля электрона.
Решение. Длина волны де Бройля для частицы зависит от её импульса р и определяется формулой
, (1)
где h - постоянная Планка.
Импульс частицы можно определить, если известна её кинетическая энергия Т. Связь импульса с кинетической энергией различна для нерелятивистского случая (когда кинетическая энергия частицы много меньше её энергии покоя) и для релятивистского случая (когда кинетическая энергия сравнима с энергией покоя частицы).
В нерелятивистском случае
, (2)
где m0 -масса покоя частицы.
В релятивистском случае
, (3)
где E0=m0c2 - энергия покоя частицы.
Формула (1) с учётом соотношений (2) и (3) запишется:
в нерелятивистском случае
, (4)
в релятивистском случае
. (5)
Сравним кинетическую энергию электрона, прошедшего заданную в условии задачи разность потенциалов Δφ, с энергией покоя электрона. В зависимости результатов сравнения решим, какую из формул (4) или (5) следует применить для вычисления длины волны де Бройля.
Как известно, кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов Δφ, равна
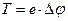, (6)
где е =1,6∙10-19 Кл – заряд электрона.
Выполним расчеты по формуле (6), учитывая, что 1 эВ=1,6∙10-19Дж:
.
