Квантовая природа излучения 2 страница

Разность потенциалов между обкладками U=Ed. Подставив числовые значения, получим U =2×10^-4×4×10^-3=80 В.

Энергия поля конденсатора W=CU²/2=ee₀SU²/2d.

Подставим числовые значения:

W =1×8,85×10^-12×10^-2×80²/(2×4×10^-3)=7,08×10^-8 Дж.

Объемная плотность энергии поля w=W/V=W/(S×d), где V=S×d - объем поля конденсатора. Выполним расчеты:

w =7,08×10^-8/(10^-2×4×10^-3)=1,77×10^-3 Дж/м³.

Ответ: E =20 кВ/м, U =80 В, W =7,08×10^-8 Дж, w =1,77×10^-3 Дж/м³.

Пример 4.В медном проводнике сечением S= 6 мм² и длиной l =5 м течет ток. За t= 1 мин в проводнике выделяется Q= 18 Дж теплоты. Определить напряженность поля, плотность и силу электрического тока в проводнике.

Решение. Для решения задачи используем законы Ома и Джоуля-Ленца. Закон Ома в дифференциальной форме имеет вид:

j=gE, (1)

где j - плотность тока; E - напряженность поля; g - удельная проводимость. Закон Джоуля-Ленца:

Q=I²Rt. (2)

Здесь I - сила тока, t - время,

R=rl/S, (3)

R - сопротивление проводника, r, l и S - удельное сопротивление, длина и площадь поперечного сечения проводника соответственно.

Силу тока I находим из (2) с учетом (3):

.

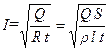Выполним проверку размерности

.

Выполним расчеты:

.

По определению плотность тока равна j=I/S. Отсюда

j =4,6/(6×10^-6)=7,7×10⁵ А/м².

Напряженность поля в проводнике определим из (1), учитывая, что g=1/r: E=j×r; E =7,7×10⁵×1,7×10^-8=1,3×10^-2 В/м.

Ответ: E =1,3×10^-2 В/м, , j =7,7×10⁵ А/м².

 

Пример 5.Внутреннее сопротивление аккумулятора r =2 Ом. При замыкании его одним резистором сила тока равна I₁ =4 А, при замыкании другим - I₁ =2 А. Во внешней цепи в обоих случаях выделяется одинаковая мощность. Определить ЭДС аккумулятора и внешние сопротивления.

Решение. Воспользуемся законом Ома для полной цепи:

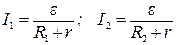, (1)

где r - внутреннее сопротивление источника тока; e - ЭДС аккумулятора; R₁ и R₂ - внешние сопротивления цепей. Уравнения (1) представим в виде:

e=I₁(R₁+r), e=I₂(R₂+r). (2)

Из равенств (2) следует

I₁(R₁+r)= I₂(R₂+r). (3)

Мощность, выделяемую во внешней цепи в первом и втором случаях, находим: N₁=I²₁R₁, N₂=I²₂R₂.

Из условия равенства мощностей следует

I²₁R₁=I²₂R₂. (4)

Решая совместно уравнения (3) и (4), получаем

R₁=I₂r/I₁, R₂=I₁r/I₂. (5)

Выполним расчеты:

R₁ =2×2/4=1 Ом; R₂ =4×2/2=4 Ом.

Подставляя (5) в (2), получаем

e=I₁r(I₂/I₁+1) e =4×2×(2/4+1)=12 В.

Ответ: e =12 В, R₁ =1 Ом; R₂ =4 Ом.

 

 

Пример 6. ЭДС батареи равна 20 В. КПД батареи составляет 0.8 при силе тока 4 А. Чему равно внутреннее сопротивление батареи?

Решение. КПД источника тока h равен отношению падения напряжения во внешней цепи к его ЭДС:

h=RI/e, (1)

откуда

R=he/I (2)

Используя выражение закона Ома для замкнутой цепи I=e/(R+r), получаем

h=R/(R+r) (3)

Подставляя (2) в (3) и выполнив преобразования, находим

r=e(1-h)/I

Выполним расчеты: r=20×(1-0,8)/4=1 Ом

 

Пример 7. На рисунке изображено сечение двух прямолинейных бесконечно длинных проводников с токами I₁ = 10 А и I₂ = 4 А., идущими к нам от чертежа. Расстояние между ними r = 0,7 м. В какой точке прямой, проходящей через эти проводники, индукция магнитного поля этих токов равна нулю? Среда – воздух.

Рисунок 2 - Сечение двух проводников

Решение. Обозначим r₁ расстояние между точкой М, в которой индукция магнитного поля этих токов равна нулю, и проводником с током I₁. (см.рис.2). Ток силой I₁ создает в точке М магнитное поле, вектор индукции которого направлен вверх. Вектор индукции магнитного поля тока I₂ в этой же точке направлен вниз. Согласно условию задачи индукция результирующего магнитного поля в точке М равна нулю. Это возможно только в том случае, когда модули векторов и равны,

т.е. В₁=В₂, где

и .

Тогда

, , ,

откуда

.

Произведем вычисления: .

Ответ:

 

 

Пример 8. В однородном магнитном поле индукцией В₁=200 мТл находится круговой виток диаметром D=8 см и сопротивлением R=0,022 Ом. Плоскость витка перпендикулярна магнитным линиям. Какой заряд q пройдет через поперечное сечение проводника, если индукция магнитного поля равномерно уменьшается до В₂=0?

Решение. При изменении магнитного потока сквозь площадь, ограниченную контуром, в нем возникнет индукционный ток силой I_i. По закону Ома , где - ЭДС индукции и R – сопротивление проводника, из которого изготовлен контур.

При прохождении индукционного тока по контуру его поперечное сечение площадью S_сеч пересекает в течении времени Δt заряда q.

Согласно определению силы тока .

Тогда , откуда .

По закону Фарадея для электромагнитной индукции

.

Здесь и - магнитные потоки, пересекающие плоскость контура. Поскольку согласно условию В₂=0, то Ф₂=0. Угол α между нормалью к плоскости контура и магнитной линией согласно условию тоже равен нулю, поэтому .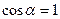

С учетом этого . Здесь - площадь витка.

Таким образом, .

Тогда .

Проверим размерность:

Произведем вычисления:

.

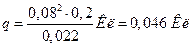Ответ:

 

Пример 9.Пройдя ускоряющую разность потенциалов U =3,52 кВ, электрон влетает в однородное магнитное поле перпендикулярно линиям индукции. Индукция поля B =0,01 Тл, радиус траектории r =2 см. Определить удельный заряд электрона.

Решение. Удельным зарядом частицы называется величина, равная отношению заряда к массе частицы, т.е. q_e/m.

В магнитном поле с индукцией на электрический заряд, который движется со скоростью , действует сила Лоренца:

. (1)

Так как частица влетает в магнитное поле перпендикулярно силовым линиям, то a =90⁰ и sina =1. Тогда (1) примет вид

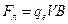. (2)

Под действием этой силы электрон перемещается по окружности и приобретает нормальное ускорение, направленное к центру окружности. Запишем второй закон Ньютона для частицы в магнитном поле:

. (3)

Кинетическую энергию электрон приобретает за счет работы сил электростатического поля:

. (4)

Преобразуя выражения (3) и (4) и исключив из них скорость, получим формулу для определения удельного заряда электрона:

.

Проверим размерность полученной формулы:

.

Выполним расчеты:

q_e/m =2×3,52×10³/(10^-4×4×10^-4)=1,76×10¹¹ Кл/кг.

Ответ: q_e/m =1,76×10¹¹ Кл/кг.

 

Пример 10. При выключении электрической цепи, содержащей катушку индуктивности и сопротивление R =5 Ом сила тока уменьшилась в 5 раз за время t =0,16 с. Определить индуктивность катушки.

Решение. При выключении электрической цепи, содержащей катушку индуктивности, сила тока убывает по закону

, (1)

где I₀ и I – сила тока в цепи в начальный момент времени (t =0) и через время t после выключения; L – индуктивность катушки, R – активное сопротивление цепи. Прологарифмируем уравнение (1)

. (2)

Выполнив преобразования (2), находим искомую величину .

Проверим размерность формулы: .

Выполним расчеты:

.

Ответ: .

 

 

Таблица вариантов

Вариант	Номера задач

Контрольная работа №1

1 В вершинах равностороннего треугольника со сторонами r=4 см находятся равные заряды по q=3 нКл. Определить напряженность поля в точке, лежащей на середине стороны треугольника.

2 Расстояние между двумя точечными зарядами q₁=+330 нКл и q₂=-330 нКл равно r=1 см. Найти напряженность поля в точке, находящейся на перпендикуляре, восстановленном к середине линии, соединяющей оба заряда на расстоянии L=1 см от нее.

3 Два точечных заряда q₁=30 нКл и q₂=-10 нКл находятся в воздухе на расстоянии r=10 см друг от друга. Определить напряженность поля, создаваемого этими зарядами в точке, удаленной на r₁=9 см от положительного заряда и r₂=7 см от отрицательного заряда. Решение пояснить рисунком.

4 В вершинах квадрата со стороной a=1 м расположены заряды одинаковой величины. В случае, когда два соседних заряда положительные, а два других - отрицательные, напряженность поля в центре квадрата равна Е=36 В¤м. Определить величину заряда.

5 В вершинах квадрата со стороной a=1 м помещены заряды по q=1 нКл. Определить напряженность поля в центре квадрата, если один из зарядов отличается по знаку от остальных.

6 Пространство между двумя параллельными бесконечными плоскостями с поверхностной плотностью зарядов s₁=+4×10^-8 Кл/м² и s₂=-7×10^-8 Кл/м² заполнено диэлектриком с диэлектрической проницаемостью e=6. Определить напряженность поля между плоскостями и вне плоскостей.

7 Расстояние между двумя параллельно расположенными бесконечно длинными металлическими нитями равно r₀=10 см. Одна нить заряжена с линейной плотностью t₁=6×10^-5 Кл/м, а другая – t₂=3×10^-5 Кл/м. Найти напряженность поля в точке, удаленной на расстояние r=10 см от каждой нити. Решение пояснить рисунком.

8 В центре металлической полой сферы, радиус которой R=4 см, расположен точечный заряд q₁=10 нКл. Заряд q₂=40 нКл равномерно распределен по поверхности сферы. Определить напряженность поля в точках, удаленных от центра сферы на расстояние r₁=2 см и r₂=8 см. Решение пояснить рисунком.

9 Поверхностная плотность заряда на бесконечной равномерно заряженной плоскости равна s=3×10^-10 Кл/м². Вычислить поток вектора напряженности через поверхность сферы диаметром D=1 м, рассекаемой этой плоскостью пополам.

10 На вертикальной бесконечной заряженной плоскости закреплена нить с шариком массой m=2 г, имеющим заряд q=+2×10^‑8 Кл. Натяжение нити, на которой подвешен шарик, равно F=4,9×10^‑4 Н. Найти поверхностную плотность заряда плоскости.

11 Бесконечная равномерно заряженная плоскость с поверхностной плотностью заряда s=4×10^‑5 Кл/м² и точечный заряд q=10 нКл находятся на расстоянии r₁=0,5 м. Какую работу необходимо совершить, чтобы сблизить их до расстояния r₂=0,2 м?

12 Определить потенциал ₁ в начальной точке перемещения заряда q₁=‑60 нКл, движущегося в поле заряда q₂=+40 нКл, если энергия, затраченная на перемещение заряда, равна W=6×10^‑5 Дж, а потенциал конечной точки ₂=1500 В. Найти, на каком расстоянии находились заряды в начале и в конце перемещения.

13 Протон, двигаясь в электрическом поле, приобрел скорость V=400 м¤с. Какую ускоряющую разность потенциалов он пролетел?

14 В поле заряда q₁=+2,2×10^-6 Кл перемещается заряд q₂=-30 нКл. Вычислить работу, совершаемую полем, если заряд перемещается между точками с напряженностью Е₁=400 В/м и Е₂=2×10⁴ В/м.

15 Два заряда q₁=100 нКл и q₂=10 нКл находятся на расстоянии r₁=40 см друг от друга. Какую работу необходимо совершить, чтобы сблизить их до расстояния r₂=15 см?

16 Определить потенциал точки поля, находящейся на расстоянии r=5 см от центра заряженного шара, если напряженность поля в этой точке равна Е=3×10⁵ В/м. Рассчитать величину заряда шара.

17 Два точечных заряда по q=10 нКл каждый находятся на расстоянии r₁=1 м друг от друга. Вычислить потенциал в точке поля, находящейся на середине расстояния между зарядами. Какую работу необходимо совершить, чтобы сблизить заряды до расстояния r₂=0,5 м?

18 Два одинаковых заряда находятся в воздухе на расстоянии r=10 см друг от друга. Напряженность поля в точке, удаленной на расстояние r₁=6 см от одного и r₂=8 см от другого заряда, равна Е=1 кВ¤м. Определить потенциал поля в этой точке и значение зарядов.

19 Пылинка массой m=4×10^{-15 кг удерживается в равновесии между горизонтально расположенными обкладками плоского конденсатора. Разность потенциалов между обкладками} Dj=245 В, а зазор между ними d=1 см. Определить, во сколько раз заряд пылинки больше элементарного заряда.

20 Заряд q=1 нКл переносится из бесконечности в точку, находящуюся на расстоянии r=1 см от поверхности металлической сферы радиусом R=5 см, заряженной с поверхностной плотностью s=10^-5 Кл/м². Определить работу перемещения заряда.

21 Разность потенциалов между пластинами плоского конденсатора Dj=6 кВ. Определить энергию и объемную плотность энергии конденсатора, если расстояние между пластинами d=0,02 м, а площадь каждой из них S=100 см².

22 Электрон, пройдя ускоряющую разность потенциалов Dj=10⁴В, попадает в плоский конденсатор длиной L=10 см и в начальный момент движется параллельно пластинам на одинаковом расстоянии от них. Расстояние между пластинами d=2 см, разность потенциалов между ними Dj=300 В. Определить вертикальное смещение электрона при вылете из конденсатора.

23 Со скоростью V=2×10⁷ м/с электрон влетает в пространство между обкладками плоского конденсатора в середине зазора в направлении, параллельном обкладкам. При какой минимальной разности потенциалов Dj на обкладках электрон не вылетит из конденсатора, если длина конденсатора L=10 см, а расстояние между его обкладками d=1 см?

24 Конденсатор с парафиновым диэлектриком емкостью С=4,42×10^‑11 Ф заряжен до разности потенциалов Dj=150 В. Напряженность поля внутри конденсатора Е=600 В¤м. Определить площадь пластин конденсатора, энергию поля конденсатора и поверхностную плотность заряда на пластине.

25 Конденсатор емкостью С₁=3 мкФ зарядили до разности потенциалов Dj₁=300 В, а конденсатор емкостью С₂=2 мкФ - до Dj₂=200 В. После зарядки конденсаторы соединили параллельно. Найти разность потенциалов на обкладках конденсаторов после их соединения.

26 Площадь пластин плоского слюдяного конденсатора S=11,3 см², зазор между ними d=3 мм. При разряде конденсатора выделилась энергия W=10 мкДж. До какой разности потенциалов был заряжен конденсатор?

27 Плоский воздушный конденсатор заряжен до разности потенциалов Dj=100 В. Площадь пластин конденсатора S=11,3 см², а расстояние между ними d=5 мм. Определить, как изменятся емкость, энергия и объемная плотность энергии конденсатора, если зазор заполнить парафином?

28 Объемная плотность энергии заряженного слюдяного конденсатора w=106 Дж/м³. Какова напряженность поля конденсатора?

29 Обкладки плоского воздушного конденсатора площадью S=100 см² и зарядом q=4 мкКл раздвигают на Dd=1 см. Определить совершаемую при этом работу.

30 Воздушный конденсатор емкостью С=0,01 мкФ заряжен до Dj=20 кВ. При разряде конденсатора разрядником 20% энергии рассеивается в виде звуковых и электромагнитных волн. Определить количество теплоты, выделяемой в разряднике.

31 Какое напряжение можно дать на катушку, имеющую N=1000 витков медного провода со средним диаметром витков d=6 см, если допустимая плотность тока j=2 А/мм²?

32 Аккумулятор замыкается один раз таким сопротивлением, что сила тока в электрической цепи, образованной аккумулятором и сопротивлением, равна I₁=3 А, а второй раз таким сопротивлением, что сила тока равна I₂=2 А. Определить ЭДС аккумулятора, если мощность тока во внешней цепи в обоих случаях одинакова, а внутреннее сопротивление аккумулятора равно r=4 Ом.

33 ЭДС батареи равна e=18 В. КПД батареи составляет h=0,9 при силе тока I=4,5 А. Чему равно внутреннее сопротивление батареи?

34 В железном проводнике длиной L=2 м и площадью поперечного сечения S=0,4 мм² идет ток. При этом за минуту выделяется теплота Q=48 Дж. Определить напряженность электрического поля в проводнике.

35 Моток медной проволоки с площадью поперечного сечения S=0,1 мм² имеет массу m=0,3 кг. Определить сопротивление проволоки.

36 На концах проводника длиной L=6 м поддерживается разность потенциалов U=120 В. Каково удельное сопротивление проводника, если плотность тока в нем j=5×10^‑8А¤м²?

37 Определить ЭДС аккумуляторной батареи, ток короткого замыкания которой I_КЗ=10 А, если при подключении к ней резистора сопротивлением R=9 Ом сила тока в цепи равна I=1 А.

38 Определить заряд, прошедший по резистору с сопротивлением R=1 Ом, при равномерном возрастании напряжения на концах резистора от U₁=1 В до U₂=3 В в течение времени t=10 с.

39 Определить количество теплоты, выделяющееся в резисторе за первые две секунды, если сила тока в нем за это время возрастает по линейному закону от I₁=0 до I₂=4 А. Сопротивление резистора R=10 Ом.

40 Электропечь выпаривает за время t=5 мин V=1 л воды, взятой при температуре t=20^оС. Какова длина нихромовой проволоки, из которой намотана печь, сечением S=0,5 мм², если печь работает под напряжением U=120 В и ее КПД h=80%?

41 Рамка диаметром D=6 см содержит N=100 витков. Плоскость витков совпадает с направлением напряженности однородного магнитного поля. равной Н=15 А/м. Какой вращающий момент М действует на рамку при пропускании через нее тока I=10 А?

42 Нормаль к плоскости рамки составляет угол a=30⁰ с направлением однородного магнитного поля. Под каким углом установилась рамка по отношению к полю, если вращающий момент, действующий на рамку, уменьшился в 10 раз?

43 Плоская круглая рамка диаметром D=10 см находится в однородном магнитном поле. По рамке протекает ток силой I=20 А. На сколько изменится вращающий момент, действующий на рамку, при повороте плоскости рамки на угол Dj=60⁰ (до поворота плоскость рамки совпадала с направлением поля). Напряженность магнитного поля равна Н=20 А/м, среда - воздух.

44 Плоская круглая рамка состоит из N=20 витков радиусом R=2 см и по ней течет ток в I=1 А. Нормаль к рамке составляет угол a=90⁰ с направлением магнитного поля напряженностью Н=30 А/м (среда -воздух). Найти изменение вращающего момента, действующего на рамку, если из 20 витков рамки сделать один круглый виток.

45 По двум бесконечно длинным прямолинейным проводникам, расположенным параллельно друг другу на расстоянии R₁=20 см, текут в одном направлении токи силой I₁=1 и I₂=5 А. Определить магнитную индукцию поля в точке, удаленной на расстояние R₂=10 см от каждого проводника.

46 По кольцевому проводнику радиусом R₁=20 см течет ток силой I₁=5 А. Параллельно плоскости кольца на расстоянии R₂=5 см над его центром проходит бесконечно длинный прямолинейный проводник, по которому течет ток I₂=3 А. Определить напряженность магнитного поля в центре кольца (рассмотреть все возможные случаи направления токов).

47 По двум бесконечно длинным прямолинейным параллельным проводникам текут токи I₁=5 А и I₂=10 А в одном направлении. Геометрическое место точек, в котором индукция магнитного поля равна нулю, находится на расстоянии R=10 см от проводника с меньшим током. Определить расстояние между проводниками.

48 По двум бесконечно длинным прямолинейным параллельным проводникам, расстояние между которыми R=50 см, в одном направлении текут токи I₁=5 А и I₂=10 А. Определить расстояние от проводника с меньшим током до геометрического места точек, в котором индукция магнитного поля равна нулю.

49 Два круговых витка с током лежат в одной плоскости и имеют общий центр. Радиус большого витка R₁=12 см, меньшего R₂=8 см. Напряженность поля в центре витков равна Н=50 А/м, если токи текут в одном направлении, и нулю, если в противоположном. Определить силы токов, текущих по круговым виткам.

50 Два круговых витка с током диаметром по D=10 см каждый лежат во взаимно перпендикулярных плоскостях так, что центры витков совпадают. Определить индукцию магнитного поля в центре витков, если по одному течет ток I₁=5 А, а по другому I₂=10 А (среда - воздух).

51 Незакрепленный проводник массой m=1 г и длиной L=7,8 см находится в равновесии в горизонтальном магнитном поле напряженностью Н=10⁵ А/м. Определить силу тока в проводнике, если он перпендикулярен линиям индукции магнитного поля.

52 Два параллельных бесконечно длинных проводника с токами I=5 А взаимодействуют с силой F=0,5 Н на 1 м их длины. На каком расстоянии находятся проводники?

53 Какое ускорение приобретает проводник массой m=1 г и длиной L=8 см в однородном магнитном поле напряженностью Н=1000 А/м, если сила тока в проводнике I=1 А, а направления тока и индукции магнитного поля взаимно перпендикулярны?

54 Проводник длиной L=50 см, по которому течет ток силой I=1 А, движется со скоростью V=1,5 м/с перпендикулярно линиям индукции магнитного поля напряженностью Н=20 А/м. Определить работу по перемещению проводника за время t=10 мин.

55 Частица с энергией W=16 МэВ движется в однородном магнитном поле с индукцией В=2,4 Тл по окружности радиусом R=24,5 см. Определить заряд частицы, если ее скорость равна V=2,72×10⁷ м/с.

56 Каким образом необходимо расположить прямолинейный алюминиевый проводник в однородном горизонтальном магнитном поле с индукцией В=0,04 Тл и какой силы ток пропустить по нему, чтобы он находился в равновесии. Радиус проводника R=1 мм.

57 Момент импульса протона в однородном магнитном поле напряженностью Н=2×10⁴ А/м равен L=6,6×10^{-23 кг}×м²¤с. Найти кинетическую энергию протона, если он движется перпендикулярно линиям магнитной индукции поля.