В настоящее время моделирование автоматических систем вообще и электроприводов в частности, основанное на применении ЦВМ, в связи с широким применением микропроцессорной техники в системах управления практически полностью вытеснило моделирование при помощи аналоговых машин. Объясняется это большей точностью цифровых моделей и возможностью использования моделей различной степени сложности в зависимости от требуемой их адекватности и допустимой погрешности.
При построении цифровой модели для аналоговых частей системы управления производится переход от аналоговой модели к цифровой, при этом происходит переход от дифференциальных уравнений к разностным уравнениям с последующим решением этих уравнений на ЦВМ.
Существует несколько методов перехода к данному виду уравнений:
1. Классические методы численного интегрирования дифференциальных уравнений. Данные методы предназначены для решения дифференциальных уравнений первого порядка вида:
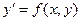, (11.1)
Уравнения более высокого порядка производной и системы уравнений представляются в виде системы уравнений в нормальной форме Коши.
2. Методы составления разностных схем для уравнения (11.1) основаны на решении уравнения вида:
, (11.2)
то есть, по сути, на решении задачи получения определенного интеграла от функции y΄(x). Наиболее известными методами получения разностных схем являются экстраполяционный и интерполяционный методы Адамса, дающие многошаговые методы решения уравнения (11.2), и метод Рунге-Кутта, из которого получаются одношаговые методы интегрирования уравнения (11.2).
3. Методы, основанные на векторно-матричном исчислении, т.е. представлении системы в пространстве состояний. Линейная система в пространстве состояний описывается следующими уравнениями:
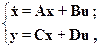, (11.3)
где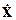 
- вектор состояния системы;
u - вектор управления;
y - выходной вектор;
A - матрица состояния системы;
B - матрица управления;
С - матрица наблюдения;
D - матрица сквозной передачи управления.
Общее решение данной системы определяется как:
, (11.4)
где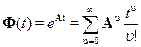 
-переходная (фундаментальная) матрица, определяющая фундаментальную систему решений однородного уравнения 
.
При цифровом моделировании наибольшее распространение получили численные методы решения уравнения (11.4) на основании следующего рекуррентного алгоритма вычисления:
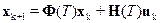, (11.5)
где T - шаг вычисления;
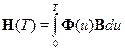- входная матрица.
Основной задачей в данном методе является нахождение переходной матрицы с определенной точностью, поскольку точно такая матрица может быть представлена разложением в бесконечный ряд, а также соответственно и входная матрица. В принципе уравнения (11.3) можно проинтегрировать и любым классическим численным методом, т.к. эта система уравнений, записанных в форме Коши.
Результаты изучения переходных процессов в физических системах на основе методов, в которых непрерывные сигналы при расчете заменяются временными последовательностями чисел, показывают, что такой подход дает значительную экономию вычислительных затрат и позволяет получить алгоритмы моделирования, в значительной мере лишенные указанных недостатков.
Соотношения между временными последовательностями действительных чисел (решетчатыми функциями) описываются удобными с вычислительной точки зрения рекуррентными разностными уравнениями, коэффициенты которых зависят от параметров физических систем. Поэтому методы, основанные на использовании свойств решетчатых функций, были названы рекуррентными разностными методами.
Теоретическая основа, обычно используемая для анализа систем, работающих в непрерывном режиме, это интегральные преобразования Лапласа и Фурье, эквивалентный метод для дискретных систем есть метод z -преобразования. Этот метод совместно с методом модифицированного z -преобразования является точным методом анализа дискретных систем.
Достоинство этого метода заключается в том, что выходную величину дискретной системы во временной области можно записать в виде удобных для вычисления рекуррентных разностных уравнений, для составления которых нет необходимости в контурном интегрировании z -изображения выходной величины.
При уменьшении периода прерывания дискретные системы по своим динамическим свойствам приближаются к непрерывным системам, а рекуррентные уравнения, описывающие их поведение во временной области, могут рассматриваться как дискретная аппроксимация дифференциальных уравнений, описывающих соответствующую непрерывную систему.
