Звено, описываемое дифференциальным уравнением
, (3.52)
называется реальным дифференцирующим звеном или инерционно-дифференцирующим звеном. Преобразуя уравнение (3.52) по Лапласу и определив отношение изображения выходной величины к входной, получим передаточную функцию:
, (3.53)
Такое звено получается в результате встречно-параллельного включения пропорционального и интегрирующего звеньев так, как это показано на рисунке 3.5, а.
Реализовать инерционно-дифференцирующее звено на операционном усилителе можно, если принять:
, (3.54)
, (3.55)
Тогда получим передаточную функцию:
, (3.56)
где 
, 
.
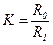Схема реализации интегро-дифференцирующего звена на операционном усилителе приведена на рисунке 3.5, б.
Инерционно-дифференцирующее звено можно реализовать также в виде четырехполюсника, представленного на рисунке 3.5, в. В этом случае передаточную функцию определим как отношение выходного и входного комплексных сопротивлений:
, (3.57)
где 
, 
.
Частотная передаточная функция
, (3.58)
Разделяя на вещественную и мнимую части, получим:
, (3.59)
Амплитудно-фазовая частотная характеристика показана на рисунке 3.5,г. Она представляет собой полуокружность, лежащую в первом квадранте (звено создает опережающий эффект) и имеющую диаметром отрезок действительной оси от 0 до K.
Амплитудная и фазовая частотные характеристики звена (рисунок 3.5,д,е)
, (3.60)
, (3.61)
Логарифмическая амплитудная частотная характеристика имеет вид:
, (3.62)
и показана на рисунке 3.5, ж пунктирной линией.
Уравнение низкочастотной части характеристики получим, пренебрегая v2T2 по сравнению с единицей:
, (3.63)
Это уравнение прямой с угловым коэффициентом +20дб/дек, имеющую при частоте сопряжения 
ординату, равную 20 lg K. Уравнение высокочастотной асимптоты получим, пренебрегая единицей по сравнению с v2T2
, (3.64)
Это уравнение описывает горизонтальную прямую, пересекающуюся с низкочастотной асимптотой при частоте v с.
Учитывая (3.63) и (3.64) получим уравнение асимптотической ЛАХ
, (3.65)
Так же как и для апериодического звена, погрешность при замене точной ЛАХ (L) асимптотической (La) (рисунок 3.5, ж) имеет максимальное значение при частоте сопряжения и равна примерно 3 дб.
ЛАХ инерционно-дифференцирующего звена приведена на рисунке 3.5,з.
Сравнивая (3.30) и (3.65), можно заключить, что частотные характеристики идеального и реального дифференцирующего звена сближаются в области низких частот и расходятся в области высоких частот.
Переходная функция имеет вид
, (3.66)
и показана на рисунке 3.5,и.
Рисунок 3.5 Характеристики инерционно-дифференцирующего звена
Форсирующее звено
Форсирующим называется звено, которое описывается дифференциальным уравнением:
, (3.67)
Этому дифференциальному уравнению соответствует передаточная функция:
, (3.68)
Видно, что передаточная функция форсирующего звена обратна передаточной функции инерционного звена.
Форсирующее звено может быть представлено как сумма пропорционального и интегрирующего звена так, как это показано на рисунке 3.6, а. Форсирующее звено может быть реализовано с помощью операционного усилителя (рисунок 3.6, б), если
, (3.69)
, (3.70)
Тогда получим передаточную функцию
, (3.71)
где: 
, .
Частотная передаточная функция звена
, (3.72)
Этой функции соответствует амплитудно-фазовая частотная характеристика (рисунок 3.6, в) в виде прямой параллельной оси ординат и отстоящей от нее на расстоянии U(v)=K.
Амплитудная частотная характеристика
, (3.73)
Фазовая частотная характеристика
, (3.74)
Эти характеристики представлены соответственно на рисунке 3.6, г, д. Логарифмическая амплитудная частотная характеристика форсирующего звена первого порядка
, (3.75)
Приближенно эта характеристика может быть заменена асимптотической, состоящей из двух отрезков:
, (3.76)
Из выражений (3.73)¸(3.76) и (3.41)¸(3.49) следует, что все выражения, выведенные для ЛАХ и ЛФХ апериодического звена, остаются справедливыми и для форсирующего звена первого порядка, если только учесть перемену знака. ЛАХ и ЛФХ форсирующего звена первого порядка показаны на рисунке 3.6, е, ж. Видно, что ЛАХ и ЛФХ форсирующего звена могут быть получены, как зеркальное отображение кривых (рисунок 3.6, ж, з) относительно оси частот.
Переходная и весовая функции форсирующего звена могут быть представлены как суммы соответствующих простейших звеньев (рисунок 3.1, ж, з) и (рисунок 3.3, ж).
, (3.77)
, (3.78)
где d(t)=1¢(t) - производная от дельта - функции или d -функция второго порядка. Производная от d -функции представляется в виде двух импульсов противоположного направления, интервал между которыми e стремится к нулю.
Рисунок 3.6 Характеристики форсирующего звена
