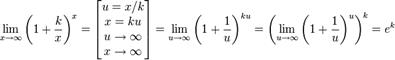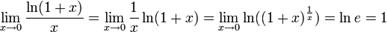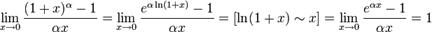Если функция f(x) непрерывна на отрезке [a; b], то множеством ее значений является отрезок [m; M], где m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a; b].
Упражнения
1.) Доказать, что последовательность может иметь не более одного предела.
Пусть limn®¥xn = A1 и limn® ¥xn = A2, A1¹ A2, тогда выберем e - окрестности точек A1, A2, так чтобы они не пересекались. В качестве e можно взять число e = 1/2|A1-A2|. По определению предела $ N1,N2, что при n>N1 xnÎU(A1), а при n>N2 xnÎ U(A2). Следовательно, при n> max{N1,N2} xnÎ U(A1)ÇU(A2), что невозможно, так как U(A1)Ç U(A2) = Æ.
2.) Доказать, что 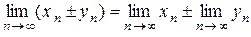 .
.
 = a,
= a,  = b, cn=xn+yn
= b, cn=xn+yn
 =c и c=a+b (т.е. что он существует и равен сумме пределов)
=c и c=a+b (т.е. что он существует и равен сумме пределов)
 = a, значит xn=а+б.м.1
= a, значит xn=а+б.м.1
 b, значит yn=b+б.м.2
b, значит yn=b+б.м.2
cn=xn+yn=a+b+б.м.3 (сумма конечного числа бесконечно малых есть бесконечно малое)
следовательно cn имеет придел и он равен сумме пределов.
3) Доказать, что произведение бесконечно малой и ограниченной последовательности есть бесконечно малая последовательность.
{xn}-б.м.п.
{yn}-ограниченная последовательность
$M>0 такое, что "n выполняется | yn |≤M и для " ε/M>0, $N такой, что для всех n≥N выполняется |xn*yn|=|xn|*|yn|< (ε/M)*M= ε=> произведение {xn}*{yn} – бесконечно малая последовательность.
4.) Доказать, что если все члены последовательности неотрицательны (положительны), то ее предел – неотрицательный.
Т.к. предел алгебраической суммы двух, трех и вообще определенного числа переменных равен алгебраической сумме пределов этих переменных, то последовательность предел последовательности ux можно расписать так: lim(u1 + u2+... + uk) = lim u1+lim u2 +... +lim uk
Доказательство. Проведем доказательство для двух слагаемых, так как для любого числа слагаемых оно проводится также. Пусть lim u1 =a1 и lim u2 = a2. Тогда на основе теоремы (если функция f(x) представлена в виде суммы постоянного числа b и бесконечно малой  y=b+
y=b+  , то lim y =b(при х->a;x->∞))
, то lim y =b(при х->a;x->∞))
u1 =a1+α1 , u2 =a2+α2 , гдеα1 и α2 –бесконечно малые,
значит u1+ u2=(a1+ a2) +(α1+α2)
т.к. (a1+ a2)- величина постоянная, а (α1+α2) – бесконечно малая, то можем заключить согласно теореме(если функция f(x) представлена в виде суммы постоянного числа b и бесконечно малой  y=b+
y=b+  , то lim y =b(при х->a;x->∞)), что
, то lim y =b(при х->a;x->∞)), что
lim(u1+ u2 )=a1+ a2 = lim u1+ lim u2
А т.к. для любого х, элемент ux>0,то и соответственно их сумма будет положительной
5) Доказать, что если сходящиеся последовательности{x n } и {y n } удовлетворяют условию x n ≥y n, то  ≥
≥ 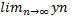
Пусть x n ≥0,  ),тогда имеем
),тогда имеем  ≥0.
≥0.
Допустим, что b <0, но тогда имеем |x n -  ≥|
≥|  |.
|.
Т.е. |x n - b| не стремится к 0 при n->∞тогда и x n не стремится к b при n->∞,значит b≥0
Таким же образом имеем для y n≥0
А потом и для x n и y n≤0
Зная, что x n ≥y n то (x n -y n)>0,то и  >0
>0
=> 
 0
0
 ≤
≤ 
6) Доказать лемму о двух милиционерах.
Если u≤z≤v, и  = b;
= b;  =b, то
=b, то 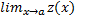
Доказательство: из u≤z≤v следует, что u-b ≤z-b ≤ v-b, из условия 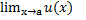 = b;
= b;  =b, следует, что при " ε найдется некоторая окрестность в точку а, в которой будет выполняться неравенство|u-b|< ε, так же найдется некоторая окрестность с центром в точке а, в которой будет соблюдаться неравенство|v-b|< ε
=b, следует, что при " ε найдется некоторая окрестность в точку а, в которой будет выполняться неравенство|u-b|< ε, так же найдется некоторая окрестность с центром в точке а, в которой будет соблюдаться неравенство|v-b|< ε
В меньшей из указанных окрестностях будут выполняться неравенства:
– ε<u-b< ε
– ε<v-b< ε=>будут выполняться неравенства – ε<u-b< ε=> 
7) Доказать, что сумма 2х бесконечно больших последовательностей одного знака является б.б.п. того же знака.
Пусть {x n } и {y n } – бесконечно большие последовательности одного знака,тогда
{x n }: "А>0, $N1€ множеству натуральных чисел такое, что "n>N1, |xn|>A
{y n }: "А>0, $N2€ множеству натуральных чисел такое, что "n>N2, |yn|>A
Возьмем N=max(N1,N2)
Тогда "n>N имеем: |xn+yn|≤|xn| + |yn|>2A, "A>0,
Т.к. sgn xn≤sgn yn, где sgn x = 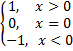
8) Доказать, что сумма бесконечно большой и ограниченной последовательностей является б.б.п.
Пусть
{an}-б.б.п. тогда $ М>>0, $N€ множеству натуральных чисел такие, что |аn|>>M, "n>N, имеем |an|> М
{bn} – ограниченная последовательность: $М1>0, |bn|≤M1, "n € множеству натуральных чисел.
M>>M1
Возьмем -|bn|≥-M
Тогда |аn|-|bn|> М1 -M; " n >0 т.к. |cn|= |аn|-|bn| >(М1 –M)>>0
Так как выражение верно для "n>N, где N€ множеству натуральных чисел, то |cn|-б.б.п.
9) Доказать,что произведение 2х б.б.п. является б.б.п.
Т.к. {an}-б.б.п. тогда $ М1>>0, $N€ множеству натуральных чисел такие, что |аn|>>M1, "n>N, имеем |an|> М1
Т.к. {bn}-б.б.п. тогда $ М2>>0, $N€ множеству натуральных чисел такие, что |bn|>>M2, "n>N, имеем |bn|> М2
Тогда |cn|=|аn|*|bn|> М1* М2>>0, "n>N, где N€ множеству натуральных чисел
10) Доказать что произведение б.б.п. и отделимой от нуля ограниченной последовательности является б.б.п.
Пусть
{an}-б.б.п. тогда $ М>>0, $N€ множеству натуральных чисел такие, что |аn|>>M, "n>N, имеем |an|> М
{bn} – ограниченная последовательность: $М1>0, |bn|≤M1, "n € множеству натуральных чисел.
M>>M1
Тогда |аn|*|bn|> М1 *M; " n >0 т.к. |cn|= |аn|*|bn| >(М1 *M)>>0
Так как выражение верно для "n>N, где N€ множеству натуральных чисел, то |cn|-б.б.п.
11) Уметь доказывать по определению, что  ,где{x}-некоторая заданная сходящаяся последовательность
,где{x}-некоторая заданная сходящаяся последовательность
"ε >0 $ N(ε) такое, "n>N выполняется |xn-A|< ε
- ε<xn-A< ε
A- ε<xn< ε+A
Xn->A
12 ) Уметь доказывать по определению, что  ,где{x}-некоторая заданная бесконечно большая последовательность
,где{x}-некоторая заданная бесконечно большая последовательность
Пусть М>>0, тогда $N€ множеству натуральных чисел такие, что |xn|>M, "n>N, т.е. все члены последовательности за исключением,может быть, конечного их числа находятся в ε-окрестности точки∞
13) Уметь доказывать по определению, что  ,гдеf(x)-некоторая заданна функция
,гдеf(x)-некоторая заданна функция
"ε >0, $δ(ε)>0 такое, что при х, удовлетворяющему неравенству 0<|x-x0|<δ
Выполняется |f(x)-А|<ε
14) Уметь доказывать по определению, что  ,гдеf(x)-некоторая заданна функция
,гдеf(x)-некоторая заданна функция
Пусть М>>0, тогда существуют N€ множеству натуральных чисел такие, что f(x)>M, "n>N, т.е. все члены функции находятся в ε-окрестности точки ∞
16.) Доказать, что сумма двух бесконечно больших функций одного знака является бесконечно большой того же знака.
Пусть даны f(x) и g(x) – бесконечно большие функции. Тогда пусть φ(x)- их сумма, т.е.
φ(х)= f(x) + g(x). Из этого равенства следует что |φ(х)|>|f(x)| и |φ(х)|>|g(x)|. Тогда
 и
и  т.к.
т.к. 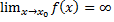 и
и


 . Отсюда можем сказать что φ(х)- бесконечно большая функция. Ч.т.д.
. Отсюда можем сказать что φ(х)- бесконечно большая функция. Ч.т.д.
18.) Доказать, что произведение двух бесконечно больших функций является бесконечно большой функцией.
Пусть даны f(x) и g(x) – бесконечно большие функции. Тогда пусть φ(x)- их произведение, т.е.
φ(х)= f(x) * g(x). Из этого равенства следует что |φ(х)|>|f(x)| и |φ(х)|>|g(x)|. Тогда
 и
и  т.к.
т.к. 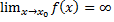 и
и


 . Отсюда можем сказать что φ(х)- бесконечно большая функция. Ч.т.д.
. Отсюда можем сказать что φ(х)- бесконечно большая функция. Ч.т.д.
19.) Доказать следствия первого замечательного предела.


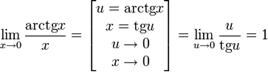

20.) Доказать следствия второго замечательного предела.