Свойство 1. Произведение бесконечно малой функции  при
при  и функции
и функции 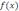 , ограниченной в некоторой
, ограниченной в некоторой  -окрестности точки a, есть функция бесконечно малая.
-окрестности точки a, есть функция бесконечно малая.
Доказательство. Функция  является ограниченной в некоторой окрестности точки a и, следовательно, существует такое число B > 0, что
является ограниченной в некоторой окрестности точки a и, следовательно, существует такое число B > 0, что

| (4) |
для всех x, удовлетворяющих условию
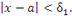
| (5) |
Поскольку функция  является бесконечно малой при
является бесконечно малой при  , то для любого произвольно малого числа ε > 0 существует такое число
, то для любого произвольно малого числа ε > 0 существует такое число 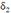 , что неравенство
, что неравенство

| (6) |
выполняется для всех x, удовлетворяющих условию

| (7) |
Выберем из чисел 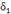 и
и 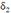 наименьшее и обозначим его символом δ. Тогда условие
наименьшее и обозначим его символом δ. Тогда условие

| (8) |
является более сильным, чем условия (5) и (7) и поэтому влечет неравенства (4) и (6).
Таким образом, для любого произвольно малого числа ε > 0 выполняется неравенство
 для всех x из δ-окрестности точки a.
для всех x из δ-окрестности точки a.
Свойство 2. Сумма двух бесконечно малых функций есть функция бесконечно малая.
Доказательство. Пусть ε > 0 – произвольно малое число;  и
и  – бесконечно малые функции при
– бесконечно малые функции при 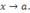 . Тогда существуют такие положительные числа
. Тогда существуют такие положительные числа  и
и  , что условия
, что условия
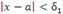
| (9) |
и

| (10) |
влекут за собой соответствующие неравенства  и
и 
Если  , то условие
, то условие  перекрывает оба условия (9) и (10) и, следовательно,
перекрывает оба условия (9) и (10) и, следовательно, 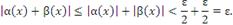
Следствие. Сумма любого конечного числа бесконечно малых функций есть функция бесконечно малая.
6.) Бесконечно большие функции: определение, свойства.
ОПРЕДЕЛЕНИЕ 1 (на языке e-d).
Функцию f(x) называют бесконечно большой при x->x0 (в точке x0 )если "М>0, $ d такое, что если х€U*(x0, d), то |f(x)|>M.
Замечание: условие |f(x)|>M означает, что f(x)€U(∞;1/M)=> записывают:  =∞; f(x)-> ∞, при x->x0
=∞; f(x)-> ∞, при x->x0
Геометрическая интерпретация
ОПРЕДЕЛЕНИЕ 2(на языке последовательностей)
Функция f(x) –б.б. при x->x0, если для любой последовательности {xn} значений аргумента, стремящейся к х0, соответствующая последовательность значений функции {f(xn)}стремится к∞
Определения 1 и 2 эквивалентны
Свойства:
1) Если f(x) –б.б. при x->x0 , то функция  – бесконечно малая при x->x0.
– бесконечно малая при x->x0.
Если f(x) – б.м. при x->x0 , то функция  – бесконечно большая при x->x0 (связь бесконечно малой и бесконечно большой функции.)
– бесконечно большая при x->x0 (связь бесконечно малой и бесконечно большой функции.)
2) Если f(x) и g(x) б.б. одного знака, то и сумма f(x)+g(x) тоже б.б. того же знака при x->x0.
3) Если f(x) – б.б. при x->x0, g(x) ограничена в некоторой окрестности U*(x0 , d), то и сумма f(x)+g(x) тоже б.б. того же знака при x->x0.
4) Если f(x) и g(x) б.б. одного знака, то и произведение f(x)*g(x) тоже б.б. того же знака при x->x0.
5) Если f(x) – б.б при x->x0,а g(x) имеет предел при x->x0 , причем  =a≠0, то их произведение f(x)*g(x)- б.б при x->x0
=a≠0, то их произведение f(x)*g(x)- б.б при x->x0
6) Если f(x) – б.б при x->x0, "x€U*(x0 , d) имеет место неравенство |f(x)|≤|g(x)|, то функция g(x)- б.б. при х->х0
7) Пусть f(x) иg(x)-б.б. одного знака при x->x0 и $ d такое, что f(x)≤£(x)≤g(x), "x€U*(x0 , d), тогда функции £(x)- б.б. того же знака при x->x0 (лемма о 2х милиционерах)
7.) Односторонние пределы. Теорема о существовании  .
.
Число AÎℝ называется пределом функции f(x) при x, стремящемся к x0 слева (в точке x0 слева), если "e>0 $d>0 такое, что если x удовлетворяет условию
0 < x 0 – x < d, то f (x)ÎU(A, e).
2) Число B Îℝ называется пределом функции f (x) при x, стремящемся к x 0 справа, если "e>0 $d>0 такое, что если x удовлетворяет условию
0 < x – x 0 < d, то f (x)ÎU(B, e).
3) Говорят, что предел функции f (x) в точке x 0 слева равен +¥ ( –¥ ) (функция стремится к +¥ ( –¥ ) при x, стремя-щемся к x 0 слева), если " M >0 $d>0 такое, что если x удовлетворяет условию 0 < x 0 – x < d, то f (x) > M (f (x) < – M).
4) Говорят, что предел функции f (x) в точке x 0 справа равен +¥ ( –¥ ), если " M >0 $d>0 такое, что, если x удовлетворяет условию 0 < x – x 0 < d, то f (x) > M (f (x) < – M).
ТЕОРЕМА 5 (необходимое и достаточное условие существования предела f (x) при x ® x 0 и x 0Îℝ).
Функция f (x) имеет предел (конечный) при x ® x 0Û существуют конечные и равные между собой односторонние пределы функции f (x) при x ® x 0. При этом 
1) необходимость
Пусть для lim f(x)=A (x->x0), тогда  такое, что f(x)
такое, что f(x) 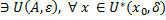
Тогда по определению  ={x
={x  , Следаовательно f(x)
, Следаовательно f(x)  удволетворяет неравенство
удволетворяет неравенство 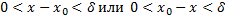 => lim f(x)=A (x->
=> lim f(x)=A (x-> 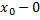 ) lim f(x)=A (x->
) lim f(x)=A (x->  )
)
2 Достаточность
lim f(x)(x-> 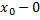 ) = lim f(x) (x->
) = lim f(x) (x->  ) =A
) =A
Тогда  f(x)
f(x) 
 ,
,  f(x)
f(x) 


Тогда если 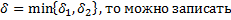 одно неравенство по модулю то есть
одно неравенство по модулю то есть
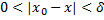 значит
значит 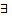 lim f(x)=A (x->
lim f(x)=A (x->  ) учитывая что
) учитывая что  f(x)
f(x) 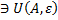
8.) Замечательные пределы и их следствия






