Второй замечательный предел

Доказательство:

Докажем вначале теорему для случая последовательности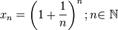

По формуле бинома Ньютона: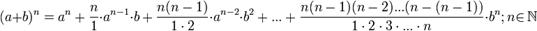

Полагая 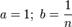получим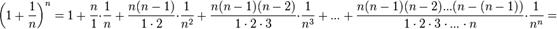

 

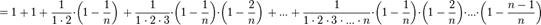
Из данного равенства (1) следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число убывает, поэтому величины возрастают. Поэтому последовательность возрастающая, при этом 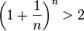(2)*Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство

Усилим полученное неравенство, заменим 3,4,5, …, стоящие в знаменателях дробей, числом 2: 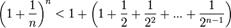Сумму в скобке найдём по формуле суммы членов геометрической прогрессии: Поэтому (3)*

Итак, последовательность ограничена сверху, при этом выполняются неравенства (2) и (3): Следовательно, на основании теоремы Вейерштрасса (критерий сходимости последовательности) последовательность монотонно возрастает и ограниченна, значит имеет предел, обозначаемый буквой e. Т.е.

Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что . Рассмотрим два случая:

 

1. Пусть Каждое значение x заключено между двумя положительными целыми числами: 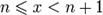,где 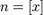— это целая часть x. => =>

Если ,то Поэтому, согласно пределу Имеем

По признаку (о пределе промежуточной функции) существования пределов

2. Пусть . Сделаем подстановку − x = t, тогда

Из двух этих случаев вытекает, что для вещественного x.

Следствия:

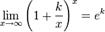
9 .) Сравнение бесконечно малых. Теорема о замене бесконечно малых на эквивалентные в пределе и теорема о главной части бесконечно малых.

 

Пусть функции a(x) и b(x) – б.м. при x ® x ₀.

ОПРЕДЕЛЕНИЯ.

1) a(x) называется бесконечно малой более высокого порядка чем b (x) если

Записывают: a(x) = o(b(x)).

2) a(x) и b(x) называются бесконечно малыми одного порядка, если

где С Îℝ и C ¹ 0.

Записывают: a(x) = O (b(x)).

3) a(x) и b(x) называются эквивалентными, если

Записывают: a(x) ~ b(x).

4) a(x) называется бесконечно малой порядка k относи-
тельно бесконечно малой b(x), если бесконечно малые a(x) и (b(x))^k имеют один порядок, т.е. если

где С Îℝ и C ¹ 0.

ТЕОРЕМА 6 (о замене бесконечно малых на эквивалентные).

Пусть a(x), b(x), a₁(x), b₁(x) – б.м. при x ® x ₀. Если a(x) ~ a₁(x), b(x) ~ b₁(x),

то

Доказательство: Пусть a(x) ~ a₁(x), b(x) ~ b₁(x), тогда

=

ТЕОРЕМА 7 (о главной части бесконечно малой).

Пусть a(x) и b(x) – б.м. при x ® x ₀, причем b(x) – б.м. более высокого порядка чем a(x).

 

= , a так как b(x)– более высокого порядка чем a(x),то 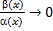, т.е. из ясно, что a(x) + b(x) ~ a(x)

 

10) Непрерывность функции в точке(на языке пределов эпсилон-дельта,геометрическое) Односторонняя непрерывность. Непрерывность на интервале, на отрезке. Свойства непрерывных функций.

1. Основные определения

Пусть f (x) определена в некоторой окрестности точки x ₀.

ОПРЕДЕЛЕНИЕ 1. Функция f (x) называется непрерывной в точке x ₀ если справедливо равенство

 

Замечания.

1) В силу теоремы 5 §3 равенство (1) можно записать в виде

 

Условие (2) – определение непрерывности функции в точке на языке односторонних пределов.

2) Равенство (1) можно также записать в виде:

 

Говорят: «если функция непрерывна в точке x ₀, то знак предела и функцию можно поменять местами».

ОПРЕДЕЛЕНИЕ 2 (на языке e-d).

Функция f (x) называется непрерывной в точке x ₀ если "e>0 $d>0 такое, что

если x ÎU(x ₀, d) (т.е. | x – x ₀ | < d),

то f (x)ÎU(f (x ₀), e) (т.е. | f (x) – f (x ₀) | < e).

Пусть x, x ₀ Î D (f) (x ₀ – фиксированная, x – произвольная)

Обозначим: D x = x – x ₀ – приращение аргумента

D f (x ₀) = f (x) – f (x ₀) – приращение функции в точкеx ₀

ОПРЕДЕЛЕНИЕ 3 (геометрическое).

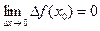Функция f (x) на зывается непрерывной в точке x ₀ если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е.

 

Пусть функция f (x) определена на промежутке [ x ₀; x ₀ + d) (на промежутке (x ₀ – d; x ₀]).

ОПРЕДЕЛЕНИЕ. Функция f (x) называется непрерывной в точке x ₀ справа (слева), если справедливо равенство

 

Очевидно, что f (x) непрерывна в точке x ₀ Û f (x) непрерывна в точке x ₀ справа и слева.

ОПРЕДЕЛЕНИЕ. Функция f (x) называется непрерывной на интервал е (a; b) если она непрерывна в каждой точке этого интервала.

Функция f (x) называется непрерывной на отрезке [ a; b ] если она непрерывна на интервале (a; b) и имеет одностороннюю непрерывность в граничных точках (т.е. непрерывна в точке a справа, в точке b – слева).

 

11) Точки разрыва, их классификация

ОПРЕДЕЛЕНИЕ. Если функция f (x) определена в некоторой окрестности точки x ₀, но не является непрерывной в этой точке, то f (x) называют разрывной в точке x ₀, а саму точку x ₀ называют точкой разрыва функции f (x).

Замечания.

1) f (x) может быть определена в неполной окрестности точки x ₀.

Тогда рассматривают соответствующую одностороннюю непрерывность функции.

2) Из определения Þ точка x ₀ является точкой разрыва функции f (x) в двух случаях:

а) U(x ₀, d)Î D (f), но для f (x) не выполняется равенство

б) U^*(x ₀, d)Î D (f).

Для элементарных функций возможен только случай б).

Пусть x ₀ – точка разрыва функции f (x).

ОПРЕДЕЛЕНИЕ. Точка x ₀ называется точкой разрыва I рода если функция f (x) имеет в этой точке конечные пределы слева и справа.

Если при этом эти пределы равны, то точка x ₀ называется точкой устранимого разрыва, в противном случае – точкой скачка.

ОПРЕДЕЛЕНИЕ. Точка x ₀ называется точкой разрыва II рода если хотя бы один из односторонних пределов функции f (x) в этой точке равен ¥ или не существует.

 

12) Свойства функций, непрерывных на отрезке [a,b](теоремы Вейерштрасса(без док-ва) и Коши

Теорема Вейерштрасса

Пусть функция f(x) непрерывна на отрезке [a,b], тогда

1)f(x)ограничена на [a,b]

2)f(x) принимает на промежутке [a,b] своё наименьшее и наибольшее значение

Определение: Значение функции m=f[x₁]зовется наименьшим, если m≤f(x) для любого x€ D(f).

Значение функции m=f[x₂]зовется наибольшим, если m≥f(x) для любого x€ D(f).

Наименьшее\наибольшее значение функция может принимать в нескольких точках отрезка.

f(x₃)=f(x₄)=max

Теорема Коши.

Пусть функция f(x) непрерывна на отрезке [a,b] и х – число, заключенное между f(a) и f(b),тогда существует хотя бы одна точка х₀€[a,b] такая, что f(x₀)= g

Доказательство:

Для определенности допустим, что f(a)<f(b)

Промежуток [a,b] поделим пополам точкой с на отрезки [a,c]и [c,b]

Если f(c)= g, то х₀= с

Если f(c)> g, то х₀€ [a,c]

Если f(c)< g, то х₀€ [c,b]

Если f(x)< g то поставим в соответствии точки х знак «+»

Если f(x)> g то поставим в соответствии точки х знак «-», тогда концы отрезка [a,b] имеют разные знаки

 

 

После деления отрезка ab выберем ту часть отрезка, где знаки разные и обозначим его как [a₁,b₁], тогда f(a₁)< g<f(b₁).Отрезок a₁b₁ разобьем пополам и выберем из двух частей отрезка тот, на левом конце которого значение меньше, чем g, а на правом - больше и обозначим как a₂b₂ и т.д.

Продолжая данный процесс неограниченно, получаем последовательность вложенных отрезков.

Поскольку отрезки вложены друг в друга и стягиваются, то существует х₀, которое принадлежит всем отрезкам одновременно.

Докажем, что f(x₀)= g:

Рассмотрим 2 последовательности: {a_n} –возрастающая и ограниченная; {b_n} - убывающая и ограниченная, значит они имеют предел =>

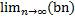
{f(an)} {f(bn)}

f(a_n)< g<f(b_n),для любого n, тогда

с учетом того, что f =f(x₀)

имеем: f(x₀)≤ g≤f(x₀), т.е. g=f(x₀)