В данной лабораторной работе исследуется САУ, где ОУ имеет сильно нелинейные свойства. Управление осуществляется с помощью пропорционального регулятора и нечеткого супервизора.
При этом объект управления с существенно нелинейными свойствами [ коэффициент
f(y) =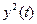 
при управляющем воздействии 
зависит от управляемой величины 
], описывается уравнением:
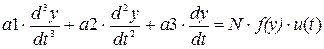. (5)
Структуру данного объекта можно представить как линейную часть с передаточной функцией
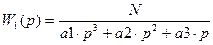, (6)
охваченную квадратичной обратной связью (рис. 6).
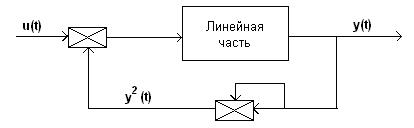
Рис. 6.
Цель управления: найти закон управления, который обеспечивал бы качественную работу системы автоматического управления при изменении рабочей точки (состоянии равновесия), т.е. значений y = const, для широкого диапазона рабочих точек (0<y<4). Обязательным является выполнение условия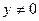 
.
Рассмотрим модель системы, в которой управление осуществляется с помощью пропорционального регулятора. Эту систему можно реализовать с помощью инструментального средства Simulink, как показано на рис. 7. Учтем, что на систему может действовать действует некоторое возмущающее воздействие g(t), которое на схеме представлено в виде блока Disturbance.
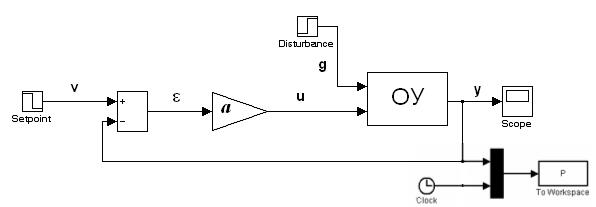
Рис. 7.
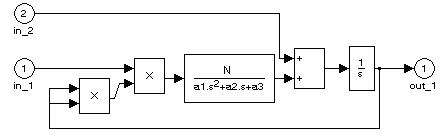
Внутренняя структура ОУ, включая линейную и нелинейную часть, может быть раскрыта с помощью рис. 8. С входа in_1 подается входное воздействие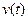 
, а с входа in_2 возмущающее воздействие g(t).
.
Рис. 8.
С помощью подбора можно найти удовлетворяющий нас коэффициент усиления пропорционального регулятора a, но только для одного входного (а соответственно и для одного выходного значения), т.е. для одной рабочей точки, например, для v(t)=1(t). Нетрудно убедиться, что, если рабочая точка изменится, то система перестанет качественно работать. В данной системе (рис. 7) нелинейность свойств вызвана коэффициентом 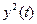при управляющем воздействии .
Чтобы исключить влияние указанной нелинейности, другими словами, осуществить точную линеаризацию ОУ [3], необходимо включить в систему блок регулировки параметров с нечетким супервизором. Разумно спроектировать нечеткий супервизор, на выходе которого формировалась бы функция
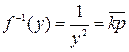. (7)
При этом коэффициент пропорционального регулятора целесообразно находить по формуле
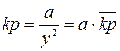, (8)
где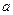 
- коэффициент усиления основного регулятора, обеспечивающий выполнение заданных требований в отношении перерегулирования или времени регулирования для v(t)=1(t). Тогда коэффициент kp можно найти по формуле (8), подставляя интересующее нас значение выходной величины y. Для конкретной системы схема, удовлетворяющая поставленной цели управления, может быть представлена в виде рис. 9.
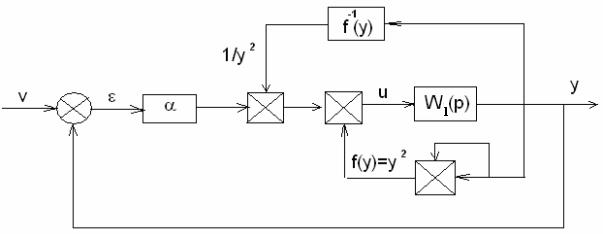
Рис. 9.
Супервизор нейтрализует нелинейность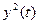 
при всех 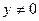, поэтому система может рассматриваться как линейная (точно линеаризованная) (см. рис. 10).
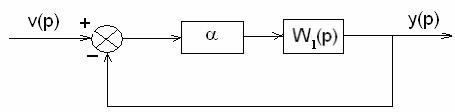
Рис. 10
Отсюда коэффициент a следует выбирать, используя структуру на рис. 10 и исходя из требований, предъявляемых к проектируемой системе.
В общем случае вид функции f(y) точно не задан. Поэтому после определения коэффициента a включаем на вход объекта еще один усилительный блок с заранее неизвестным коэффициентом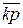 
(рис. 11). Затем, считая заданным, чему равно f(y) при y=1 (в рассматриваемом случае f(1)=1) определяем реакцию системы (рис.11) на v(t)=1(t) и находим величину перерегулирования 
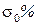, которое обычно оказывается меньше заданного значения перерегулирования для проектируемой системы. После чего для каждой требуемой рабочей точки y=yj, j=1,2,…,n, другими словами, для каждого задающего воздействия v(t)=yj1(t) находим путем симуляции модели значение коэффициента 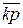j, при котором величина перерегулирования оказывается близкой к величине .
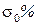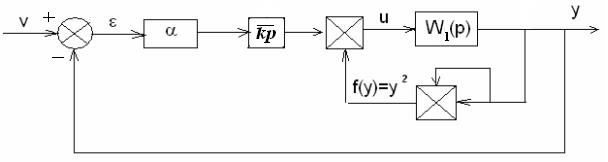
Рис.11
Полученные данные сводим в таблицу 2.
Табл. 2
| y1 | y2 | … | yn |
| 
| … | 
|
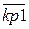
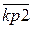
Следующий шаг – реализация супервизора, осуществляющего интерполяцию точек, определяемых Табл.2. Такой супервизор можно реализовать, применяя блок задания таблиц Lookup Table из категории Lookup Tables средства Simulink или нечеткий контроллер Такаги-Сугено. В последнем случае приходим к нечеткому супервизору.
Рис. 12 иллюстрирует, каким образом можно аппроксимировать желаемую кривую изменения коэффициента 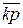(y) для n=3, т.е. используя три точки (другими словами, три правила) и тем самым осуществить нечеткое супервизорное управление. Разумеется, чтобы повысить точность аппроксимации, можно добавить еще правила, которые очевидно улучшат качество управления.
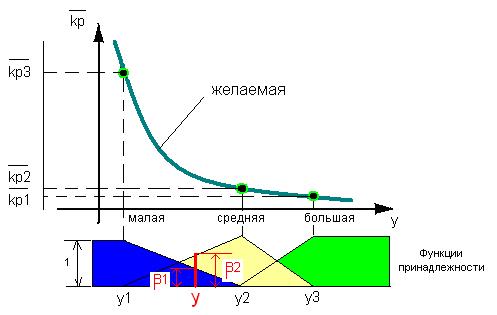
Рис. 12.
Из диапазона изменения управляемой величины y измеряются три значения y, им присваиваются характеристики малая, средняя и большая. Далее выбираются треугольные функции принадлежности. Используя полученные данные, можно составить нечеткие правила для данного случая (трех выбранных точек)(трех оредставляется действительным между ложью и истиной.:
Если управляемая величина y большая, То коэффициент усиления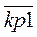 
.
Если управляемая величина y средняя, То коэффициент усиления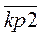 
.
Если управляемая величина y малая, То коэффициент усиления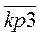 
.
При этом
, (9)
где 
, 
, 
- переменные, показывающие степень истинности данной предпосылки.
Правила не аналогичны заданию таблиц, так как нечеткая арифметика интерполирует форму нелинейной функции. Показано, что объем памяти, требуемый для хранения информации о функциях принадлежности и правил значительно меньше, чем для таблиц задания, в особенности для систем с несколькими входами, в результате чего скорость вычислений может быть повышена.
Наконец, заменяя блок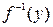 
(рис. 9) блоком задания таблиц или нечетким супервизором, получаем искомую систему, которая должна удовлетворять предъявляемым требованиям.
