Дискретные двумерные случайные величины

Опр. Двумерная СВ (X, Y) называется дискретной, если каждая из СВ и Х и Y является дискретной.

Пусть СВ Х может принимать значения , а СВ Y принимает дискретные значения .

Y X	y ₁	y ₂	…	y_m	P { X=x_i }
x ₁	P ₁₁	P ₁₂	…	P _{1 m}	P ₁ _·
x ₂	P ₂₁	P ₂₂	…	P _{2 m}	P ₂ _·
…	…	…	…	…	…
x _n	P_n ₁	P_n ₂	…	P_nm	P_n_·
P {Y =y_j }	P _·₁	P _·₂	…	P _· _m

Двумерный случайные вектор может принимать только пары значений

По этой таблице нетрудно определить функцию распределения.

33.Условные законы распределения для системы СВ. Если СВ образующие систему зависимы, то для нахождения закона распределения системы не достаточно знать законы распределения отдельных величин, входящих в систему, требуется знать так называемый условный закон распределения одной из них.

Опр Условным законом распределения одной из величин системы (X, Y) называется ее закон распределения вычисленный при условии, что другая СВ приняла определенное значение.

Начнем с наиболее простого случая, а именно со случая, когда СВ Y является дискретной.

Опр. Условной функцией распределения называется условная вероятность события

Замечание 1. Условная функция распределения обладает всеми свойствами, которые присущи обычной (т.е. безусловной) функции распределения.

Замечание 2 Если СВ X также дискретная, причем , то удобно рассматривать условную вероятность , СВ X принять значения при условии, что ,

В общем случае условную функцию распределения , однако, это не всегда возможно. Потому, что для непрерывного типа P{Y=y}=0. Чтобы отстроиться от этих неприятностей, попытаемся воспользоваться предельным переходом, заменяя событие {Y=y}, событием {y£Y<y+ D } и устремив D ® 0.

Получим.

Назовем условной функцией распределения

Оказывается такой предел всегда существует.Если СВ Y – непрерывна, то условную функцию распределения можно определить следующим выражением

В наиболее важных для приложений случаях вектор (X, Y) представляет собой двумерную непрерывную СВ с совместной плотностью .

Так как функция имеет производную по x, то мы получаем окончательное выражение для условной плотности.

36. Коэффициент корреляции. Связь между…

Опр. Величина r_XY называется коэффициентом корреляции СВ X и Y. Коэффициент r_XY характеризует степень зависимости СВ X и Y, но не любой, а только линейной зависимости, которая проявляется в том, что при возрастании одной СВ X, другая также проявляет тенденцию возрастания, в этом случае r_XY>0. Если одна возрастает, а другая убывает, то r_XY<0. В первом случае говорят, что две СВ связаны положительной корреляцией. Во втором случае говорят, что две СВ связаны отрицательной корреляцией. Модуль r_XY характеризует степень тесноты линейной зависимости между СВ X и Y. Если линейной зависимости нет, то r_XY=0.

Теорема Если же СВ X и Y связывает жесткая функциональная линейная зависимость Y=aX+b, то r_XY=1 при a>0, r_XY= –1 при a<0.

Доказательство:

;

Теорема: ï r_XY ï£1 Доказательство:

Рассмотрим СВ , тогда

;

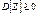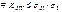
; g.

Опр. СВ X и Y называется не коррелированными, если r_XY =0 (или K_XY =0).

Замечание. Из независимости СВ следует их не коррелированность. Обратное не верно. Из коррелированности не вытекает их независимость

Теорема. D[X+Y] = D_X+D_Y+2 K_XY

Доказательство:

D[X+Y]=M[((X+Y)–(m_X– m_Y))²]= M[((X– m_X)+(Y – m_Y))²]= M[(X– m_X)²+ 2(X– m_X)(Y – m_Y)+ (Y – m_Y)²]=

D_X+D_Y+2 M[(X– m_X)(Y – m_Y)]= D_X+D_Y+2 K_XY

Следствие:

(доказательство проводится методом математической индукции).

40.Функции от многомерных СВ. Формула композиции. Функция от многомерной СВ определяется точно также, как и функция от одномерной СВ. Мы рассмотрим это понятие на примере двумерной СВ. Пусть на вероятностном пространстве (W, A, P), задана двумерная СВ (X, Y). Предположим, что у нас имеется измеренная числовая функция g(X,Y) числовых аргументов X и Y. СВ Z=g(X,Y) = g(X(w),Y(w)), назовем функцией от двумерной СВ (X, Y).

а) Функция g(X,Y) от двумерной дискретной СВ (X, Y) снова является дискретной СВ, принимающей значения g(x_i, y_j) с вероятностями P_ij=P{X=x_i,Y=y_j } Чтобы построить ряд распределения СВ Z=g(X,Y) надо:1) Исключить все те значения g(x_i, y_j), вероятность которых равна нулю; 2) Объединить в один столбец все одинаковые значения g(x_i, y_j), приписав этому столбцу суммарную вероятность.

б) В случае когда СВ (X, Y) непрерывного типа с плотностью f(x,y), функция распределения Z=g(X,Y) будет определяться формулой

Область интегрирования здесь состоит из всех точек (x, y) для которых g(X,Y)<Z. особо важным для практики представляется случай, когда X и Y – независимые СВ, а функция Z=X + Y, тогда g(x,y)=x+y. Получается так называемая формула композиции:

f_X(x) - ф-я плотности композиции от х

f_Y(y) - ф-я плотности композиции от у

f(x,y)=f_X (x) f_Y (y)

Интеграл (*) вычисляется, как повторный, поэтому

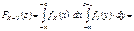
Дифференцируя по z получаем

– формулы композиции (свертки).

С помощью этих формул легко выражаются формулы плотности и функции распределения суммы независимых СВ.

42.Распределение Стьюдента. Пусть Z~N(0;1).

V– независимая от Z СВ, которая распределена по закону c² с k степенями свободы.

Рассмотрим СВ .

СВ Т имеет распределение, которое называется t –распределением или распределением Стьюдента с k степенями свободы.

t –распределение определяется одним параметром – числом степеней свободы.

С возрастанием числа степеней свободы t –распределение асимптотически (довольно быстро) приближается к стандартному нормальному распределению с параметрами (0; 1).

Для СВ, имеющих распределение Стьюдента, имеется таблица квантилей, причем в силу четности .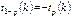

46.Выборка и способы ее представления Задачи математической статистики: Установления закономерностей, которым подчинены массовые случайные явления основано на изучении методами теории вероятностей статистических данных (результатов наблюдений) 1. Задача математической статистики: Указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально составленных экспериментов. 2. Задача математической статистики: 1) Разработать методы анализа статистических данных в зависимости от целей исследования: а) оценка неизвестной вероятности событий; б) оценка неизвестной функции распределения; в) оценка параметров распределения, вид которого известен; г) оценка зависимости СВ от одной или нескольких других СВ. 2) Проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения вид, которого известен.

Современную математическую статистику определяют как науку о принятии решений в условиях неопределенности.

Выборка и способы ее представления: Математическая статистика позволяет получить обоснованные выводы о параметрах, видах распределений и других свойствах СВ о конечной совокупности наблюдений над этими величинами.

Выборка понимается следующим образом. Пусть СВ Х наблюдается на каком либо эксперименте, повторим этот эксперимент n раз при одинаковых условиях. Получаем Х₁,.., Х_n где каждая Х_j – СВ соответствующая j -му эксперименту. Очевидно, что Х_j – независимые в совокупности СВ, причем каждая из этих СВ имеет один и тот же закон распределения, что и СВ Х.

Опр. Закон распределения СВ Х называется распределением генеральной совокупности.

СВ вектор Х₁,.., Х_n называется выборочным вектором, а конкретные числа x₁,.., x_n, получаемые на практике при n кратном повторении эксперимента в неизменных условиях представляет собой реализацию выборочного вектора и называются выборкой объема n.

Что такое вариационный ряд, размах выборки, статистический ряд, группированный статистический ряд, частоты, относительные частоты, накопленные частоты, относительные накопленные частоты, всевозможные полигоны и гистограммы, а также, что такое эмпирическая функция распределения изучили самостоятельно.

47.Числовые характеристики выборки Пусть x₁,.., x_n выборка объема n из генеральной совокупности с функцией распределения F_X(x). Рассмотрим выборочное распределение, т.е. распределение дискретной СВ, принимающей эти значения с вероятностями, равными 1/n. Соответственно числовые характеристики этого выборочного распределения называют выборочными (эмпирическими) числовыми характеристиками. Замечание. Выборочные числовые характеристики являются характеристиками данной выборки, но не являются характеристиками распределения генеральной совокупности. “~” – при обозначении этих числовых характеристик. . . – унимодального, т.е. одновершинного распределения называется элемент выборки, встречающийся с наибольшей частотой. Выборочной медианой называется , которое делит вариационный ряд на две части, содержащие равное число элементов. Если n – нечетное число, т.е. n = 2 l +1, то 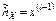. Если n – четное число, т.е. n = 2 l, то . Можно доказать, что выборочные начальные и центральные моменты порядка s для негруппированных выборок объема и определяются по следующим формулам

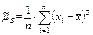; . Форма распределения СВ характеризуется выборочными коэффициентами асимметрии и эксцесса.

51. Выборочная дисперсия Докажем, что выборочная дисперсия является смещенной оценкой для дисперсии генеральной совокупности.

Выполним следующие преобразования

; .

Найдем МО для дисперсии:

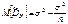МО не совпадает с s ², а отличается на –s²/n – смещение. Таким образом эта оценка занимает в среднем истинное значение дисперсии на величину s²/n, правда это смещение сходит на нет при n ® ¥.

Чтобы устранить это смещение надо «исправить» дисперсию.

;

Можно доказать, что статистика S² является и состоятельной оценкой для дисперсии генеральной совокупности. Замечание. К сожалению, на практике при оценке параметров не всегда оказывается возможным одновременное выполнение требований: несмещенности, эффективности и состоятельности.