6.1 Определение значений фазовых углов рабочего и холостого хода
В состав механизма входят два ползуна, являющихся ведомыми (выходными) звеньями. Рабочим ходом является фаза, в которой ползуны движутся в сторону, противоположную направлению силы полезного сопротивления. В нашем случае в противоположные стороны от шарнирно-неподвижной опоры. Таким образом фаза рабочего хода для ползуна D– положения механизма с 5 по 11, для ползуна В – с 0-6.
6.2 Определение Fу и Fп
Построим 12 рычагов Жуковского для определения уравновешивающей силы. Для этого используем 12 планов скоростей соответствующих построенным кинематическим схемам. Перенесем на планы скоростей все внешние силы, действующие на механизм, предварительно повернув их в противоположную сторону вращения кривошипа на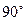 
. Поскольку сила полезного сопротивления (
) действует только при рабочем ходе, перенесем ее на те планы скоростей, которые соответствуют рабочему ходу. Уравновешивающую силу (
) перенесем в точку 
всех планов скоростей, силы тяжести - во все точки центров масс соответственно. Силы инерции и моменты пар сил инерции не учитываем.
Представим план скоростей в виде жесткой системы, закрепленной (условно) в полюсе р. Силы, приложенные к ней, создают вращающие моменты. Чтобы система находилась в равновесии, необходимо уравновесить моменты вращения. Составим уравнение равновесия:
(6.1)
6.3 Построение диаграммы приведенных моментов движущих сил
Для нахождения момента сил необходимо найти приведенную силу 
, которая по модулю равна уравновешивающей силе, но направлена в противоположную сторону. Силу уравновешивающую найдем из уравнения моментов составленного для каждого положения механизма, относительно полюса (6.1).
Составим уравнения моментов для каждого положения механизма:
0,12) 
1) 
2) 
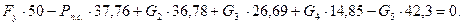
3) 
4) 
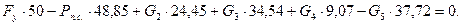
5) 
6) 
7) 
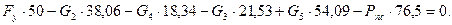
8) 
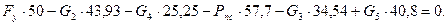
9) 
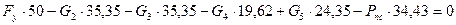
10) 
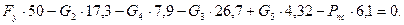
11) 
Из последних равенств найдем величины уравновешивающей силы (
) для всех двенадцати положений механизма:
0, 12) 
1) 
2) 
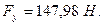
3) 
4) 
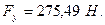
5) 
6) 
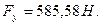
7) 
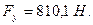
8) 
9) 
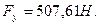
10) 
11) 
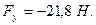
Отрицательные значения уравновешивающих сил говорят о том, что необходимо изменить направление силы в противоположную сторону.
Определяем силу приведения (
):
Для нулевого положения:
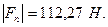
Для остальных положений расчет ведется аналогично.
Момент приведенных сил для нулевого положения найдем по формуле:
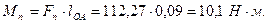
где - приведенная сила, Н;
- длина звена 
, м.
Аналогично рассчитываем силу приведения и момент приведенных сил (, 
) для остальных положений механизма, и сводим их в одну таблицу 5.
Таблица 5 – Силы приведения и моменты приведенных сил
| Положения механизма | Расчетная величина | ||
| 
| 
| |
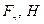
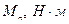
| 0, 12 | -112,27 | 112,27 | 10,1 |
| 27,94 | -27,94 | -2,51 | |
| 147,98 | -147,98 | -13,32 | |
| 246,72 | -246,72 | -22,2 | |
| 275,49 | -275,49 | -24,79 | |
| 121,74 | -121,74 | -10,95 | |
| 585,58 | -585,58 | -52,7 | |
| 810,1 | -810,1 | -72,9 | |
| 727,15 | -727,15 | -65,44 | |
| 507,61 | -507,61 | -45,68 | |
| 182,77 | -182,77 | -16,45 | |
| -21,8 | 21,8 | 1,96 |
Для построения диаграммы приведенных моментов сил рассчитываем масштабные коэффициенты.
Масштабный коэффициент оси угла поворота:
где L - произвольно выбранное расстояние от 0 до 12 положения механизма на диаграмме, мм.
Масштабный коэффициент оси момента приведенных сил:
где 
- максимальный момент приведенных сил (см. таблицу 5), Н·м;
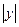- расстояние, изображающее максимальный момент приведенных сил на диаграмме, мм.
Переведем все приведенные моменты через масштабный коэффициент в линейные значения:
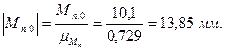
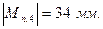
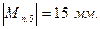
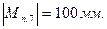
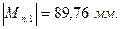
При построении диаграммы по оси ординат (
) отложим произвольно выбранный отрезок 
. По оси абсцисс () откладываем значения приведенных моментов 
в соответствующих положениях. При чем выше оси значение со знаком «-», а ниже со знаком «+».
Соединив все точки плавной лекальной кривой, получаем кривую изменения приведенного момента движущих сил.
Приведенный момент сил сопротивления является величиной постоянной, и высчитывается по формуле:
Для построения кривой изменения приведенного момента сил сопротивления переведем полученную величину в масштабный коэффициент:
По полученному значению построим прямую приведенного момента сил сопротивления.
6.4 Построение диаграммы работ движущих сил и сил сопротивления
Для построения диаграммы работ используем диаграмму приведенных моментов. Для этого замеряем величину момента приведенных сил в точках, расположенных по середине между соседними положениями механизма. Данную величину делим на коэффициент уменьшения (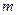
) и откладываем на диаграмме работ. Для последующих положений величину отрезка прибавляем к полученной ранее, также уменьшая в раз и откладывая на диаграмме. Соединяя все отложенные точки плавной кривой, получаем диаграмму работ движущих сил (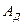
). Соединяя начальную и конечную точки прямой линией, получим диаграмму сил сопротивления (
).
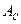Рассчитываем масштабный коэффициент работ:
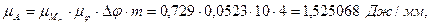
где 
- интервал между соседними положениями по оси ;
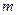- коэффициент уменьшения;
- масштабный коэффициент момента приведенных сил;
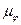- масштабный коэффициент угла поворота.
6.5 Построение диаграммы изменения кинетической энергии
Масштабный коэффициент оси изменения кинетической энергии:
Для определения области нахождения графика по формуле найдем значение:
, (6.2)
где 
- изменения кинетической энергии, Дж;
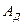- работа движущих сил, Дж;
- работа сил сопротивления, Дж.
Для построения диаграммы изменения кинетической энергии измерим расстояния между линиями работы движущих сил и сил сопротивления и отложим эти значения выше или ниже оси угла поворота кривошипа в зависимости от знака. Соединим отложенные точки плавной кривой.
6.6 Построение диаграммы приведенных моментов инерции
Приведенный момент инерции механизма будет складываться из постоянной величины (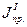
) и переменной (
):
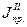(6.3)
Найдем постоянную величину ():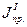
, (6.4)
где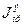 
- момент инерции энергетической машины, кг·м2;
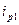- передаточное отношение преобразующего механизма;
- момент инерции кривошипа (рабочей машины), кг·м2.
Найдем момент инерции кривошипа ():
где m1 - масса кривошипа, кг;
(lOA)- длина кривошипа, м.
Для вычисления приведенного момента инерции энергетической машины необходимо подобрать электродвигатель.
В качестве электродвигателя возьмем двигатель серии 4А.
Рассчитаем частоту вращения и мощность двигателя:
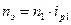
Примем передаточное отношение равным 4 (
). Тогда:
По полученным значениям подберем стандартный электродвигатель с ближайшими наибольшими характеристиками.
Возьмем двигатель 4А80А4 (N=1,1 кВт, n=1420 об/мин). Приведенным момент инерции ротора этого двигателя равен:
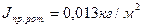
Найдем приведенный момент инерции энергетической машины, исключив влияние магнитного поля земли:
Подставляя полученные значения в формулу (6.4), получим:
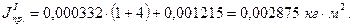
Найдем переменную величину ():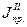
, (6.5)
где 
- угловая скорость кривошипа, с-1;
- сумма энергий шатунов и ползунов.
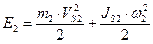- для шатуна 2;
- для ползуна 3;
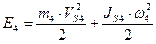- для шатуна 4;
- для ползуна 5,
где 
- скорость центра масс i-го звена;
- масса i-го звена;
- угловая скорость i-го звена;
- момент инерции шатуна i.
Скорости центров масс:
,
,
,
.
Угловые скорости кривошипа и шатунов:
, 
, 
.
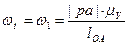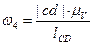Подставим значения скоростей центров масс и угловых скоростей в выражение (6.5):
Преобразуем полученное выражение. Для облегчения вычисления переменной части приведенного момента инерции для каждого положения механизма необходимо каждое слагаемое из числителя дроби представить в виде произведения квадрата длины отрезка на коэффициент ki:
,
где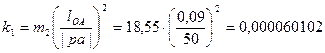 
;
;
;
;
;
.
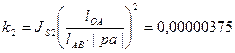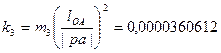Измерим длины необходимых отрезков с планов положений и рассчитаем приведенный момент инерции для каждого положения механизма.
Полученные данные сведем в таблицу 6.
Таблица 6 – значения приведенных моментов инерции
| Положение механизма | |ps2|, мм | |ab|, мм | |ps3|, мм | |ps4|, мм | |cd|, мм | |ps5|, мм |  , кг/м2
|  , кг/м2
|  , кг/м2
|  , мм
|
| 19,73 | 26,7 | 41,09 | 24,08 | 0,115282 | 0,002875 | 0,1182 | 66,67 | |||
| 33,8 | 43,12 | 19,62 | 39,09 | 62,13 | 43,06 | 0,170729 | 0,1736 | 65,85 | ||
| 45,08 | 25,6 | 37,75 | 44,78 | 77,67 | 59,83 | 0,435604 | 0,4385 | 78,78 | ||
| 66,66 | 66,66 | 0,583539 | 0,5864 | 96,05 | ||||||
| 33,98 | 43,64 | 19,54 | 64,23 | 64,46 | 0,396514 | 0,3994 | 95,37 | |||
| 43,51 | 25,61 | 37,76 | 54,24 | 58,11 | 39,97 | 0,046668 | 0,0495 | 75,37 | ||
| 19,73 | 47,61 | 66,66 | 0,297067 | 0,2999 | 66,67 | |||||
| 47,89 | 25,61 | 48,85 | 54,24 | 58,11 | 39,97 | 0,616042 | 0,6189 | 83,27 | ||
| 37,18 | 43,64 | 30,46 | 64,23 | 64,46 | 0,640540 | 0,6434 | ||||
| 66,66 | 66,66 | 0,415523 | 0,4184 | 96,05 | ||||||
| 37,18 | 43,64 | 30,46 | 60,68 | 0,147770 | 0,1506 | 83,40 | ||||
| 47,89 | 25,61 | 48,85 | 51,85 | 58,11 | 26,69 | 0,049029 | 0,0519 | 73,88 |
Определим масштабный коэффициент приведенного момента инерции по максимальному значению:
где 
- максимальный приведенный момент инерции, кг·м2;
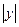- произвольно выбранный отрезок, мм.
Переведем все приведенные моменты инерции (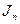
) в данный масштабный коэффициент и построим диаграмму.
Для построения диаграммы по оси абсцисс откладываем , а по оси ординат .
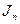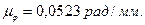
Для построения диаграммы для каждого положения откладываем соответствующие значения (
) и соединяем полученные точки плавной кривой.
6.7 Построение диаграммы энергия-масса
Построение диаграммы происходит следующим образом: по оси откладываем ординаты из диаграммы изменения кинетической энергии, а по оси - ординаты диаграммы приведенных моментов инерции, соответствующие одному и тому же положению механизма. Номера положений фиксируем на пересечении соответствующих координат диаграммы. В итоге получим замкнутую кривую.
6.8 Определение значения момента инерции маховой массы
По справочной таблице выберем коэффициент неравномерности хода ДВС:
Вычислим максимальный и минимальный угол наклона касательной:
Проведем касательные к диаграмме энергия-масса сверху и снизу под углами 
и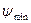 
до пересечения с осью .
Замерим отрезок 
, между точками пересечения касательных и осью изменения энергии, и определим приведенный момент инерции маховой массы:
.
