Кинематический анализ плоского рычажного механизма

 

 

3.1 Построение плана положений механизма

 

План положений – графическое изображение взаимного расположения звеньев в данный момент времени, выполненный в определенном масштабном коэффициенте.

Построим положения механизма через каждые 30 градусов вращения кривошипа, начиная от одного из крайних положений. Каждое положение строится тем же методом, что и кинематическая схема механизма. Пронумеруем положения от 0 до 12.

 

3.2 Построение планов скоростей относительно 12-ти положений ведущего звена

 

Для построения планов скоростей необходимо составить векторные уравнения скоростей.

Проанализируем полученную схему кривошипно-ползунного механизма: точка является неподвижной точкой, следовательно, модуль скорости этой точки равен нулю .

Вектор скорости точки представляет собой геометрическую сумму вектора скорости точки и скорости относительного вращательного движения точки вокруг точки :

Линия действия вектора скорости является перпендикуляром к оси кривошипа 1, а направление действия этого вектора совпадает с направлением вращения кривошипа 1.

Модуль скорости звена :

(3.1)

где V_AO – модуль скорости звена ОА, м/с;

ω₁ - угловая скорость звена , с^-1;

- длина кривошипа , м.

Для вычисления величины модуля скорости звена , нужно определить угловое ускорение данного звена по формуле:

 

(3.2)

 

где ω₁ – угловая скорость звена, с^-1;

π – 3,14;

n – количество оборотов в минуту, об/мин.

Подставив заданные значения в выражение (3.2), получим:

 

Подставив найденное значение угловой скорости в выражение (3.1), получим:

Вектор скорости точки , принадлежащей шатуну 2, представляет собой геометрическую сумму вектора скорости точки и вектора скорости относительного вращательного движения точки вокруг точки ():

 

В тоже время точка принадлежит и ползуну 3. Ползун 3 совершает прямолинейные возвратно-поступательное движение вдоль направляющей (прямой 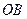),следовательно, линия действия вектора скорости точки проходит параллельно прямой :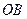

Совместное решение последних двух выражений позволит определить моду­ль и направление действия вектора скорости точки .

Вектор скорости точки Спредставляет собой геометрическую сумму вектора скорости точки А и скорости относительного вращательного движения точки С вокруг точки А ( ):

А также, геометрическую сумму вектора скорости точки Ви вектора скорости относительного вращательного движения точки С вокруг точки В ():

Совместное решение последних двух выражений позволит определить моду­ль и направление действия вектора скорости точки С.

Вектор скорости точки , принадлежащей шатуну 4, представляет собой геометрическую сумму вектора скорости точки и вектора скорости относительного вращательного движения точки вокруг точки ():

В тоже время точка принадлежит и ползуну 5. Ползун 5 совершает прямолинейные возвратно-поступательное движение вдоль направляющей (прямой ),следовательно, линия действия вектора скорости точки проходит параллельно прямой :

Совместное решение последних двух выражений позволит определить моду­ль и направление действия вектора скорости точки .

Найдем масштабный коэффициент скорости µ_V по формуле:

 

(3.3)

где µ_V – масштабный коэффициент скорости, (м/с)/мм;

- модуль скорости точки А, м/с;

- произвольно выбранный отрезок, изображающий на плане скоростей вектор скорости точки , мм.

Примем , и подставив в выражение (3.3) получим:

 

Разрешив графические векторные уравнения, строим план скоростей.

Для построения плана скоростей, найдем длину отрезка pc, изображающего на плане скорость точки С:

 

 

Отрезки, изображающие вектор скорости точек S_2,S₄ найдем, воспользовавшись теоремой подобия:

Для точки S₂: На плане скоростей в получившемся треугольнике (abc) на пересечении медиан этого треугольника находится искомая точка S₂.

Для точки S₄:

 

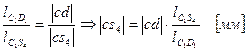
где |cd| - отрезок, изображающий на плане скоростей вектор скоростей мм.

l_CD, – длины звеньев СD, CS₄ соответственно, м.

 

 

Используя величины отрезков , , , , и , определим модули соответствующих скоростей:

Модуль скорости точки :

 

 

Модуль скорости :

 

 

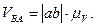
Модуль скорости точки :

 

 

Модуль скорости :

Модуль скорости точки S₂:

Модуль скорости точки S₄:

Угловая скорость кривошипа 1 по условию задания постоянная, высчитывается по формуле 3.2. Ползуны 3 и 5 совершают прямолинейные возвратно-поступательные движения, следовательно не имеют угловых скоростей. Угловая скорость шатунов 2 и 4 находится по формулам:

,

Направление угловых скоростей определяем следующим образом:

Принимаем неподвижными точки А и С для шатунов 2 и 4 соответственно, и рассматриваем движение точек В и D как вращательное относительно остановленных точек, при чем вращение должно быть направлено в сторону действия векторов 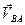и соответственно.

Направления действия угловых скоростей определим перенося в соответствующие точки вектора относительных скоростей этих точек с плана скоростей, предварительно мысленно закрепив другую точку этого звена. Направление его действия и укажет направление вращения соответствующего звена.

 

Строим планы скоростей для всех положений механизма. Вычисляем истинные величины линейных и угловых скоростей для всех положений механизма и сводим их в таблицу 2.

Таблица 2 – Значения угловых и линейных скоростей для двенадцати положений механизма

 

№ поло- жения	Скорости точек,	Угловые скорости звеньев,
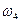
	4,29	9,85	1,14	4,40	11,44	3,89	2,23	11,12	2,38	5,83
	1,95	11,50	0,51	2,00	6,40	9,08	8,63	11,69	1,08	4,57
	0,14	11,43	0,03	0,14	0,24	11,42	11,40	11,47	0,07	0,17
	3,53	8,80	0,94	3,62	6,13	10,52	10,79	10,37	1,96	4,37
			3,06	11,79	12,21	7,30	7,86	7,74		8,72
	19,00	12,56	5,06	19,49	17,68	5,13	6,15	9,30	10,55	12,62
	11,39	14,67	3,03	11,69	18,65	4,16	6,43	12,40	6,32	13,32
	0,49	11,31	0,13	0,51	7,41	6,30	5,20	11,40	0,27	5,29
	8,56	7,40	2,28	8,78	3,46	12,47	13,13	8,90	4,75	2,47
	11,82	3,36	3,15	12,13	14,14	17,11	19,65	4,10	6,56	10,1
	10,89	1,38	2,09	11,17	16,27	12,87	15,09	8,01	6,05	11,62
	7,54	6,32	2,01	7,74	14,83	5,48	6,50	9,78	4,18	10,59
			3,06	11,79	16,38	14,79	17,26	8,50		11,7

 

 

3.3 Построение планов ускорений относительно 12-ти положений ведущего звена.

 

Для построения плана ускорений составим векторные уравнения. Вектор ускорения точки представляет собой геометрическую сумму вектора ускорения точки ,вектора нормального ускорения и вектора тангенциального ускорения относительного вращательного движения точки вокруг точки :

 

(3.4)

 

В уравнении (3.4) первое слагаемое равно нулю так как точка является неподвижной, а третье слагаемое равно нулю, так как угловая скорость звена ОА постоянна Тогда уравнение (3.4) примет следующий вид:

 

 

Модуль ускорения точки :

 

 

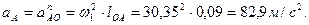
Вектор ускорения точки , принадлежащей шатуну 2, представляет собой геометрическую сумму вектора ускорения точки , вектора нормального ускорения и вектора тангенциального ускорения относительного вращательного движения точки вокруг точки :

 

 

При этом модуль вектора 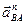находим по выражению:

 

 

В то же время точка принадлежит и ползуну 3. Ползун 3 совершает только прямолинейное возвратно-поступательное движение вдоль направляющей (прямая 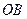), следовательно, линия действия вектора ускорения точ­ки проходит параллельно прямой :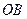

 

Вектор ускорения точки C₁, принадлежащей 2, представляет собой геометрическую сумму вектора ускорения точки А₁, вектора нормального ускорения и вектора тангенсального ускорения относительного вращательного движения точки C₁ вокруг точки А₁:

 

(2.2.5)

 

Вектор ускорения точки C₁, принадлежащей контуру 2, представляет собой геометрическую сумму вектора ускорения точки В₁, вектора нормального ускорения и вектора тангенсального ускорения относительного вращательного движения точки С₁ вокруг точки В₁:

 

Вектор ускорения точки , принадлежащей шатуну 4, представляет собой геометрическую сумму вектора ускорения точки , вектора нормального ускорения и вектора тангенциального ускорения относительного вращательного движения точки вокруг точки :

 

 

При этом модуль вектора находим по выражению:

 

 

В то же время точка принадлежит и ползуну 5. Ползун 5 совершает только прямолинейное возвратно-поступательное движение вдоль направляющей (прямая ), следовательно, линия действия вектора ускорения точ­ки проходит параллельно прямой :

 

Масштабный коэффициент ускорений:

 

(3.6)

 

где µ_а – масштабный коэффициент ускорений, м/(с²·мм);

– модуль ускорения точки , м/с²;

- произвольно выбранный отрезок, изображающий на плане ускорений вектор ускорения точки , мм.

 

Примем , тогда формула (3.6) примет вид:

 

При построении плана ускорений в качестве полюса выбираем произвольную точку p, из нее в выбранном коэффициенте проведем вектор .

Разрешив графически векторные уравнения, построим план ускорений.

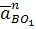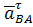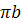Из полюса на плане ускорений, в выбранном масштабе, проведем вектор . Из конца этого вектора поведём вектор . Затем из конца вектора проведем прямую перпендикулярную отрезку АВ. Из полюса проведем вектор , а из его конца отрезок, перпендикулярный . Точка пересечения этих прямых позволит найти величины и направление векторов величины , и . 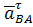Измерив длины отрезков , и и умножив их на масштабный коэффициент ускорений, в котором строится план ускорений, получим истинные значения , и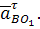

Ускорение первого звена равно 0 (), т.к. тангенсальное ускорение его точки А так же равно нулю. Пятое звено не будет иметь углового ускорения, т.к. совершает только поступательное движение вдоль направляющей стойки 0.

 

Длина отрезка, изображающего в составе плана ускорений вектор

 

 

Длина отрезка, изображающего в составе плана ускорений вектор

 

 

Длины отрезков, изображающих на плане ускорений векторы ускорений центров тяжести шатунов 2 и 4, найдем, воспользовавшись теоремой подобия:

 

откуда

,

 

 

где - отрезок из плана ускорений; l_CD, l_CS4 – длины звеньев СD, CS₄ соответственно, м.

 

 

Измерив на плане ускорений величины отрезков 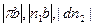и , определим модули соответствующих ускорений.

Модуль ускорения точки :

 

 

Модуль ускорения :

 

 

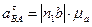
Модуль ускорений :

 

 

Модуль ускорения :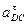

 

 

Модуль ускорений :

 

 

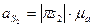
Модуль ускорений :

 

 

Угловые ускорения шатунов 2 и 4:

 

и

Угловые ускорения направлены в сторону действия тангенциального ускорения рассматриваемого звена, учитывая что точка В вращается вокруг А, а точка D вокруг С, при чем вращение должно быть направлено в сторону действия векторов и соответственно.

Направление действий угловых ускорений найдем следующим способом: переносим в соответствующие точки вектора относительных тангенсальных ускорений этих точек с плана ускорений, предварительно мысленно закрепив другую точку этого звена. Направление его действия и укажет направление углового ускорения соответствующего звена.

Угловая скорость кривошипа 1 является постоянной величиной, следовательно, угловое ускорение этого звена равно нулю, т.е. e₁ = 0. Ползуны 3 и 5 совершают только поступательные движения, следовательно, угловые ускорение этих звеньев равно нулю, т.е. e₃=e₅=0.