Структурная схема механизма

Рисунок 1.1 – Структурная схема механизма
1.1 Подвижность механизма
Подвижность механизма определяемпо формуле Чебышева:
 (1)
(1)
где W - подвижность механизма;
n - число подвижных звеньев;
p5 и p4 - соответственно число пар пятого и четвертого класса.
Для определения значений n найдем все подвижные и не подвижные звенья, входящие в состав рассматриваемого механизма. Результаты исследования заносим в таблицу 1.
Таблица 1 - Звенья механизма
| Вид движения | Схема | № звена/ название |
| неподвижное | 
| 0/ стойка |
| вращательное | 
| 1/ кривошип |
| сложное | 
| 2/ шатун |
| поступательное | 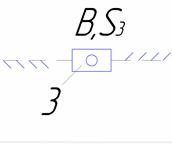
| 3/ ползун |
| сложное | 
| 4/ шатун |
| поступательное | 
| 5/ ползун |
Структурная схема механизма состоит из пяти подвижных звеньев и неподвижной стойки, представленной шарнирно-неподвижной опорой и двумя направляющими ползунов 3 и 5.
Для определения значений p4 и p5 найдем все кинематические пары, входящие в состав рассматриваемой кинематической цепи. Результаты исследования заносим в таблицу 2.
Таблица 2 – Кинематические пары
| Вид контакта/ замыкание | Класс/ подвижность | Схема КП | № звеньев/ название КП подвижность |
| Поверхн. (низш.)/геометр. | 5/1 | 
| 0-1 вращательная |
| Поверхн. (низш.)/геометр. | 5/1 | 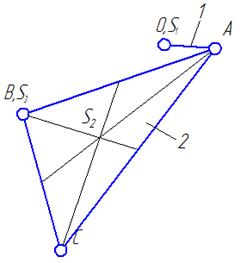
| 1-2 вращательная |
| Поверхн. (низш.)/геометр. | 5/1 | 
| 2-3 вращательная |
| Поверхн. (низш.)/геометр. | 5/1 | 
| 2-4 вращательная |
| Поверхн. (низш.)/геометр. | 5/1 | 
| 4-5 вращательная |
| Поверхн. (низш.)/геометр. | 5/1 | 
| 3-0 поступательная |
| Поверхн. (низш.)/геометр. | 5/1 | 
| 5-0 поступательная |
Из анализа данных (таблица 2) следует, что исследуемая схема кривошипно-ползунного механизма представляет собой замкнутую кинематическую цепь и состоит из семи пар пятого класса, пар четвертого класса в составе структуры нет. Следовательно, p5=7, а p4=0.
Подставив найденные значения n, p4 и p5 в формулу (1), получим:

Полученный результат означает, что для однозначного описания положения всех звеньев механизма в рассматриваемой плоскости достаточно знать одну обобщенную координату.
1.2 Анализ состава структуры механизма
Для решения данной задачи используется структурная классификация механизмов, предложенная профессором Ассуром, согласно которой плоские рычажные механизмы состоят из структурных групп звеньев и первичных (элементарных) механизмов.
Начиная с выходных звеньев – ползунов 3 и 5, разбиваем рассматриваемую схему кривошипно-ползунного механизма на группы звеньев. При этом руководствуемся следующим правилом: если выделенная группа звеньев обладает совместно нулевой подвижностью, то эта группа звеньев является структурой группой Ассура (СГА).
Количество подвижных звеньев определяет класс СГА.
Поводок – это конечное звено СГА, входящее в состав кинематической пары и имеющее свободный элемент звена.
Количество поводков определяет порядок группы, а вид СГА определяется ее структурной схемой.
Рассмотрим группу звеньев 2-3 (рисунок 1.2).

Рисунок 1.2 – Группа звеньев 2-3
Данная группа состоит из двух подвижных звеньев: шатун 2 и ползун 3, и трех кинематических пар:
1-2 вращательная пара пятого класса;
2-3 вращательная пара пятого класса;
3-0 поступательная пара пятого класса.
Следовательно, структурная формула – ВВП, являющаяся вторым видом.
Группа звеньев 2-3 является группой второго класса (так как состоит из двух звеньев и трёх кинематических пар).
Поводки представлены звеном 1 и направляющей ползуна, следовательно группа звеньев 2-3 второго порядка.
Таким образом, n=2, p5=3, а p4=0.
Подставив выявленные значения в формулу (1), получим:
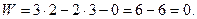
Следовательно, группа звеньев 2-3 является структурной группой Ассура второго класса, второго порядка, второго вида.
Рассмотрим группу звеньев 4-5 (рисунок 1.3).

Рисунок 1.3 – Группа звеньев 4-5
Структурная группа звеньев 4-5 образована звеньями 4 и 5, входящими в две вращательные кинематические пары 2–4 и 4-5 и одну поступательную пару 0–5, и является группой II класса (так как состоит из двух звеньев и трёх кинематических пар), второго порядка (т.к. содержит два поводка), второго вида (так как две пары вращательные и одна поступательная).
Данная группа состоит из двух подвижных звеньев: шатун 4 и ползун 5; поводка: шатун 2 и направляющая (стойка) 0; и трех кинематических пар:
2-4 вращательная пара пятого класса;
4-5 вращательная пара пятого класса;
5-0 поступательная пара пятого класса.
Таким образом, n=2, p5=3, а p4=0.
Подставив выявленные значения в формулу (1), получим:
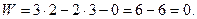
Следовательно, группа звеньев 4-5 является структурной группой Ассура второго класса, второго порядка, второго вида.
Рассмотрим группу звеньев 0-1 (рисунок 1.3).

Рисунок 1.3 – Группа звеньев 0-1
Данная группа состоит из подвижного звена кривошипа 1, стойки 0 и двух кинематических пар:
0-1 вращательная пара пятого класса
1-2 вращательная пара пятого класса
Тогда n=1, p5=1, а p4=0.
Подставив найденные значения в формулу (1), получим:

Следовательно, группа звеньев 0-1 не является структурной группой Ассура, а представляет собой первичный механизм, подвижность которого равна единице, т.е. существует одна обобщенная координата.
Вывод. Из проведенного анализа следует, что число степеней свободы механизма равно 1; механизм имеет следующий структурный состав: первичный механизм с подвижностью ровной 1 и две структурные группы Ассура 2 класса 2 порядка 2 вида.
Структурная формула механизма

Рисунок 1.4 – Структурный состав кривошипно-ползунного механизма
Класс механизма определяется наивысшим классом группы Ассура, входящей в данный механизм. Рассмотренный механизм является механизмом второго класса.




