Для проведения силового анализа воспользуемся кинетостатическим методом, основанным на принципе Даламбера (в число заданных сил при расчёте входят силы инерции), при этом определим реакции связей кинематических пар и уравновешивающую силу (уравновешивающий момент).
Для проведения силового анализа построим в заданном масштабном коэффициенте длин одно положение механизма, для которого скорости и ускорения всех звеньев не равны нулю.
Возьмем седьмое положение механизма и построим его в масштабном коэффициенте длин 
Рассчитаем силы, действующие на звенья.
Сила тяжести  равна:
равна:
 , (4.1)
, (4.1)
где Gi - сила тяжести i -го звена, Н;
 – масса i -го звена, кг;
– масса i -го звена, кг;
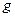 – ускорение свободного падения,
– ускорение свободного падения,  .
.
Масса звена  определяем по формуле:
определяем по формуле:
 , (4.2)
, (4.2)
где mi – масса i -го звена, кг;
 – удельная масса i -го звена, кг/м;
– удельная масса i -го звена, кг/м;
 – длина i -го звена, м.
– длина i -го звена, м.
Удельные массы равны:
для кривошипов 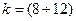 кг/м.
кг/м.
для шатунов 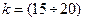 кг/м.
кг/м.
Масса ползуна рассчитывается по формуле:
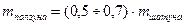 , (4.3)
, (4.3)
где mползуна – масса ползуна, кг;
mшатуна – масса шатуна, к которому прикреплен ползун, кг.
По формулам (4.2) и (4.3) определим массы звеньев:
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
По формуле (4.1) определим силы тяжести звеньев:
 ,
,
 ,
,
 ,
,
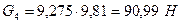 ,
,
 .
.
Откладываем вектора сил тяжести  ,
,  ,
,  ,
,  и
и  на положении механизма соответственно от точек
на положении механизма соответственно от точек  ,
,  ,
,  ,
,  и
и  .
.
Центр масс кривошипа лежит на оси вращения кривошипа.
Определим силы инерции звеньев.
Вектор силы инерции  может быть определен по формуле:
может быть определен по формуле:
 (4.4)
(4.4)
где  – вектор силы инерции i -го звена;
– вектор силы инерции i -го звена;
 – масса i -го звена, кг;
– масса i -го звена, кг;
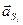 – вектор полного ускорения центра масс i -го звена.
– вектор полного ускорения центра масс i -го звена.
Как видно из формулы (4.4) вектор силы инерции направлен в противоположную сторону по отношению к вектору полного ускорения центра масс звена.
 , (4.5)
, (4.5)
где Fиi – сила инерции i -го звена, Н;
mi – масса i -го звена, кг;
аsi – полное ускорение центра масс i -го звена, м/с2.
Момент пары сил инерции направлен противоположно угловому ускорению 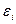 и может быть определён по формуле:
и может быть определён по формуле:
 (4.6)
(4.6)
где Миi – момент пары сил инерции i -го звена, Н·м;
Isi – момент инерции i -го звена относительно оси, проходящей через центр масс si и перпендикулярной к плоскости движения звена, кг·м2;
εi – угловое ускорение i -го звена, с-2.
Момент инерции шатуна определяется по формуле:
 (4.7)
(4.7)
Величины ускорений центров масс  ,
,  ,
,  и
и 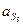 возьмем из плана ускорений.
возьмем из плана ускорений.
Рассчитаем силы инерции по формуле (4.5):





Проведем силы инерции на десятом положении механизма.
Рассчитаем моменты инерции шатунов по формуле (4.7):
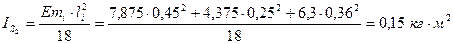 ,
,
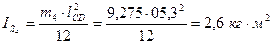 .
.
Рассчитаем моменты пар сил инерции для второго и четвертого звеньев по формуле (4.6):
 ,
,
 .
.
Покажем на чертеже моменты пар сил инерции шатунов и укажем направление силы полезного сопротивления. Далее разбиваем механизм на группы звеньев и проводим их силовой расчет.
4.1 Силовой анализ структурной группы Ассура звеньев 2-3
Рассмотрим структурную группу Ассура 2-3. Запишем уравнение кинетостатического равновесия:
 (4.8)
(4.8)
Где  и
и 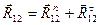 – силы реакций, приложенные соответственно к звеньям 3 и 2 со стороны звеньев, образующих кинематические пары.
– силы реакций, приложенные соответственно к звеньям 3 и 2 со стороны звеньев, образующих кинематические пары.
Запишем уравнение суммы моментов относительно точки B:

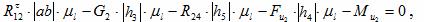
где h3 – наименьшее расстояние от линии действия силы тяжести G2 до точки В;
h4 – наименьшее расстояние от линии действия силы Fu2 до точки В.
 - наименьшее расстояние от линии действия силы R24 до точки В
- наименьшее расстояние от линии действия силы R24 до точки В

Таким образом в уравнении (4.8) осталось две неизвестных силы, их можно определить составлением векторного силового многоугольника. Для его составления воспользуемся выражением (4.8).
Подберем масштабный коэффициент сил 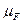 :
:
 , (4.9)
, (4.9)
где µF – масштабный коэффициент сил, Н/мм;
 – действительное значение известной максимальной силы, входящей в уравнение, Н;
– действительное значение известной максимальной силы, входящей в уравнение, Н;
 – длина вектора, изображающего максимальную силу на плане сил, мм.
– длина вектора, изображающего максимальную силу на плане сил, мм.
По формуле (4.9) определим масштабный коэффициент сил:
 .
.
Для построения силового многоугольника переведем величины всех сил в масштабный коэффициент:
 ,
,
 ,
,
 ,
,
 ,
,
 .
.

Из произвольной точки строим вектор  , потом из конца этого вектора вектор
, потом из конца этого вектора вектор  и так далее по уравнению (4.8). Завершаем многоугольник сил, проводя из начала вектора
и так далее по уравнению (4.8). Завершаем многоугольник сил, проводя из начала вектора  прямую параллельную AB, а из конца вектора
прямую параллельную AB, а из конца вектора  прямую, перпендикулярную OB. Точка пересечения позволяет построить силы
прямую, перпендикулярную OB. Точка пересечения позволяет построить силы  и
и  на плане сил и определить их истинное значение.
на плане сил и определить их истинное значение.
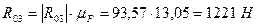 ,
,
 .
.
4.2 Силовой анализ структурной группы Ассура звеньев 4-5
Рассмотрим структурную группу Ассура 4-5. Запишем уравнение кинетостатического равновесия:
 (4.10)
(4.10)
Где 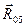 и
и  – силы реакций, приложенные соответственно к звеньям 5 и 4 со стороны звеньев, образующих кинематические пары.
– силы реакций, приложенные соответственно к звеньям 5 и 4 со стороны звеньев, образующих кинематические пары.
Запишем уравнение суммы моментов относительно точки D:


где h – наименьшее расстояние от линии действия силы тяжести G4 до точки D;
h1 – наименьшее расстояние от линии действия силы Fu4 до точки D.

Знак “-“ означает, что силу  надо направить в обратную сторону.
надо направить в обратную сторону.
Таким образом в уравнении (4.10) осталось две неизвестных силы, их можно определить составлением векторного силового многоугольника. Для его составления воспользуемся выражением (4.10).
Подберем масштабный коэффициент сил 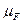 :
:
 , (4.11)
, (4.11)
где µF – масштабный коэффициент сил, Н/мм;
 – действительное значение известной максимальной силы, входящей в уравнение, Н;
– действительное значение известной максимальной силы, входящей в уравнение, Н;
 – длина вектора, изображающего максимальную силу на плане сил, мм.
– длина вектора, изображающего максимальную силу на плане сил, мм.
По формуле (4.11) определим масштабный коэффициент сил:
 .
.
Для построения силового многоугольника переведем величины всех сил в масштабный коэффициент:
 ,
,
 ,
,
 ,
,
 мм
мм

Из произвольной точки строим вектор  , потом из конца этого вектора вектор
, потом из конца этого вектора вектор  и так далее по уравнению (4.10). Завершаем многоугольник сил, проводя из начала вектора
и так далее по уравнению (4.10). Завершаем многоугольник сил, проводя из начала вектора  прямую параллельную CD, а из конца вектора
прямую параллельную CD, а из конца вектора  прямую, перпендикулярную OD. Точка пересечения позволяет построить силы
прямую, перпендикулярную OD. Точка пересечения позволяет построить силы  и
и 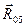 на плане сил и определить их истинное значение.
на плане сил и определить их истинное значение.
 ,
,
 .
.
4.3 Силовой анализ первичного механизма
Рассмотрим первичное звено. Запишем уравнение кинетостатического равновесия:

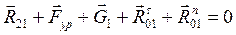 (4.12)
(4.12)
Для нахождения тангенциальной составляющей силы  составим уравнение суммы моментов относительно точки А:
составим уравнение суммы моментов относительно точки А:
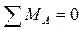 ;
;
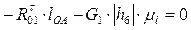
Из уравнения выразим тангенциальную составляющую силы  :
:

Запишем уравнение суммы моментов относительно точки O:




Примем масштабный коэффициент сил, для плана сил первичного механизма:

Строим многоугольник сил, для этого, сначала рассчитаем длины векторов сил на плане сил:



Из произвольной точки строим вектор  , потом из конца этого вектора вектор
, потом из конца этого вектора вектор  и так далее по уравнению (4.12). Завершают многоугольник сил, соединяя конец вектора
и так далее по уравнению (4.12). Завершают многоугольник сил, соединяя конец вектора  и начало вектора
и начало вектора 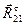 . Найдем величину силы
. Найдем величину силы  .
.

Момент управляющего воздействия: 
Теорема Жуковского
Для определения уравновешивающей силы, воспользуемся теоремой В.И. Жуковского: если механизм под действием системы силовых факторов, приложенных к характерным точкам механизма, находится в равновесии, то в равновесии будет находиться повернутый на 90º план скоростей, рассматриваемый как жесткий рычаг вращающейся вокруг полюса плана и нагруженный той же системой силовых факторов приложенных к одноименным точкам планов.
Построим для седьмого положения механизма повёрнутый на 90º по ходу вращения кривошипа план скоростей, в масштабном коэффициенте.
 .
.
На повернутый план скоростей переносим вектора сил, действующие на звенья, в соответствующие точки в том направлении, в котором они действуют. При этом приложенные к звеньям 2 и 4 моменты пар сил инерции заменяем парами сил:
 , (5.1)
, (5.1)
где  и
и 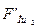 – силы, образующие пару сил, Н;
– силы, образующие пару сил, Н;
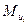 – моменты пар сил инерции i -го звена, Н·м;
– моменты пар сил инерции i -го звена, Н·м;
 – длина i -го звена, м.
– длина i -го звена, м.
Рассчитаем по формуле (5.1) пары сил, действующие на звенья:
 ,
,
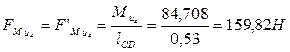 .
.
Силы  ,
,  приложены в крайних точках звена.
приложены в крайних точках звена.
Линия действия уравновешивающей силы перпендикулярна звену OA.
По методу Жуковского, сумма моментов вех сил  , включая силы инерции и уравновешивающую силу, относительно полюса плана скоростей р равна нулю:
, включая силы инерции и уравновешивающую силу, относительно полюса плана скоростей р равна нулю:
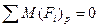 ,
,
 (5.2)
(5.2)

(5.3)
Измеряем плечи моментов на плане:
 ,
,
 мм,
мм,
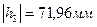 ,
,
 ,
,
 ,
,
 ,
,
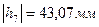 ,
,
 ,
,
 ,
,
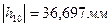 ,
,
 7,615 мм,
7,615 мм,
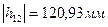



Подставляя все найденные значения в формулу (5.3) и произведем вычисления, получим:

Высчитаем момент уравновешивающей силы:

Определим относительную погрешность, допущенную при определении уравновешивающего момента двумя способами:
 , (5.4)
, (5.4)
где  ,
,  – максимальное и минимальное значения уравновешивающего момента, полученные в результате двух расчетов, Н.
– максимальное и минимальное значения уравновешивающего момента, полученные в результате двух расчетов, Н.
Подставляя полученные значения в формулу (5.3), получим:

Данная погрешность получена в результате применения графоаналитического метода расчёта и округления численных значений и является допустимой.






