Понятие непрерывной функции

Из школьного курса математики вы знакомы с понятием непрерывной функции, как функции, график которой изображается сплошной линией. Дадим формальное определение непрерывной функции.

Функция f (x) называется непрерывной в точке x ₀, если выполнены условия:

1) f (x) определена в точке x ₀, то есть определено число f (x ₀);

2) существует конечный предел ;

3) = f (x ₀).

ЗАМЕЧАНИЕ.

Если условие 1) выполнено, то условия 2) и 3) равносильны условию 4) = 0.

Действительно, если выполнены условия 1) — 3), то

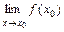= – = f (x ₀) – f (x ₀) = 0.

Обратно, если определено число f (x ₀) и = 0, то

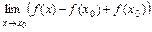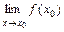= = + = f (x ₀), то есть существует конечный предел , равный f (x ₀).

Введем обозначение D x = x – x ₀. Тогда x = x ₀ + D x, f (x) = f (x ₀ + D x) и условие = 0 можно переписать в виде = 0. Если в полученном выражении заменить точку x ₀ на x, получим условие непрерывности функции f (x) в точке x: = 0. Величина D x называется приращением аргумента, а разность D y = f (x + D x) – f (x) — приращением функции f (x) в точке x. Таким образом, для непрерывной в точке x функции f (x) из стремления к нулю приращения аргумента следует стремление к нулю приращения функции.

ПРИМЕР 1. f (x) = C.

1) Функция определена в каждой точке x ₀ числовой прямой.

4) = .

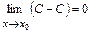Непрерывность функции f (x) = C в произвольной точке x ₀ доказана.

ПРИМЕР 2. f (x) = .

1) Функция определена в каждой точке x ₀ числовой прямой, кроме x ₀ = 0.

4) = .

Непрерывность функции f (x) = в произвольной точке x ₀ ¹ 0 доказана.

ПРИМЕР 3. f (x) =

Заметим, что на промежутках (– ¥; 0) и (0; +¥) функция f (x) является константой и, следовательно, непрерывна в любой точке x ¹ 0.

В точке x = 0 функция f (x) определена: f (0) = 0, но не имеет предела, так как

, а . Следовательно, в точке x = 0 функция f (x) не является непрерывной.

 

2. СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ В ТОЧКЕ

ТЕОРЕМА 1. Арифметические свойства непрерывных функций.

Если функции f (x) и g (x) непрерывны в точке x ₀, то их сумма f (x) + g (x), разность f (x) – g (x), произведение f (x) · g (x), а если g (x ₀) ¹ 0, то и частное непрерывны в точке x ₀.

ДОКАЗАТЕЛЬСТВО.

Докажем утверждение теоремы для суммы непрерывных функций. Так как функции f (x) и g (x) непрерывны в точке x ₀, то они определены в точке x ₀ и имеют в этой точке конечные пределы, совпадающие со значениями этих функций в точке x ₀. Следовательно, сумма f (x) + g (x) определена в точке x ₀, принимает в этой точке значение f (x ₀) + g (x ₀). Предел функции f (x) + g (x) в точке x₀ тоже существует, так как = + по теореме об арифметических свойствах пределов. А так как функции f (x) и g (x) непрерывны в точке x ₀, то получаем равенство = + = f (x ₀) + g (x ₀), которое окончательно доказывает непрерывность функции f (x) + g (x) в точке x ₀.

Для разности, произведения и частного функций теорема доказывается аналогично.

ТЕОРЕМА 2. Непрерывность суперпозиции непрерывных функций.

Пусть функция u (x) непрерывна в точке x ₀, а функция f (u) непрерывна в точке u ₀, причем u ₀ = u (x ₀). Тогда функция f (u (x)) непрерывна в точке x ₀.

Без доказательства.

Введем понятие обратной функции.

Пусть имеется функция y = f (x), имеющая область определения D и область значений E, а на множестве E определена функция x = g (y) так, что для любых чисел x ₀ Î D и y ₀ Î E, связанных соотношением y ₀ = f (x ₀), справедливо соотношение x ₀ = g (y ₀). Тогда функция g называется обратной к функции f и обозначается f ^–1. Для существования обратной функции необходимо, чтобы для каждого y значение x функции f ^–1(y) в точке y определялось однозначно, то есть для любых различных точек x ₁ ¹ x ₂ значения y ₁ = f (x ₁) и y ₂ = f (x ₂) функции f в этих точках были тоже различны: y ₁ ¹ y ₂. Это условие выполняется, если функция f (x) строго монотонна.

ТЕОРЕМА 3. Непрерывность обратной функции.

Если функция f (x) имеет обратную функцию f ^–1(y) и является непрерывной в точке x ₀, то f ^–1(y) является непрерывной в точке y ₀ = f (x ₀).

Без доказательства.

Замечание. Если функция f (x) имеет обратную функцию f ^–1(y) и является непрерывной в точке x, то из стремления к нулю приращения D y функции f (x) в этой точке следует стремление к нулю приращения ее аргумента D x.

Действительно, если D y = f (x + D x) – f (x), то D x = f ^–1(y + D y) – f ^–1(y) и, в силу непрерывности обратной функции, согласно определению непрерывной функции.

ТЕОРЕМА 4. О непрерывности элементарных функций.

Все элементарные функции непрерывны в своей области определения.

ДОКАЗАТЕЛЬСТВО.

Докажем сначала непрерывность функций y = x, y = sin x и y = e ^x.

Для y = x имеем Следовательно, функция y = x непрерывна в любой точке x.

В силу теоремы об арифметических свойствах непрерывных функций и непрерывности константы функция y = kx + b тоже непрерывна в любой точке x.

Для y = sin x имеем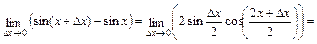

= = 1· .

Последнее равенство справедливо, так как Dx — бесконечно малая при , а y = — ограниченная функция. Следовательно, функция y = sin x непрерывна в любой точке x.

Функция y = cos x = непрерывна как суперпозиция непрерывных функций. Функции и непрерывны в своей области определения как частное непрерывных функций. Функции y = arcsin x, y = arcсos x, y = arctg x, y = arcctg x непрерывны в своей области определения как обратные к непрерывным функциям.

Для y = e ^x имеем e ^x ·1· 0 = 0. Следовательно, функция y = e ^x непрерывна в любой точке x.

Функция y = ln x непрерывна в своей области определения (x > 0) как обратная функция к непрерывной функции y = e ^x.

Функцию y = a ^x можно переписать в виде y = a ^x = . Это означает, что функция y = a ^x непрерывна в любой точке x как суперпозиция непрерывных функций.

Функцию y = log _a x можно переписать в виде y = log _a x = . Это означает, что функция y = log _a x непрерывна в любой точке x своей области определения как частное непрерывных функций.

Функцию y = x ^a с произвольным показателем a можно переписать в виде y = x ^a = . Это означает, что функция y = x ^a непрерывна в любой точке x как суперпозиция непрерывных функций.

Мы доказали непрерывность всех основных элементарных функций. Остальные элементарные функции получаются из основных элементарных функций с помощью арифметических действий или в виде суперпозиции. Следовательно, они непрерывны в своей области определения.

ТЕОРЕМА 5. О сохранении знака для непрерывных функций.

Если функция f (x) непрерывна в точке x₀ и f (x ₀) > A, где A — некоторое вещественное число, то существует окрестность U (x ₀,d) точки x ₀, для каждой точки x из которой справедливо неравенство f (x) > A.

ДОКАЗАТЕЛЬСТВО.

Поскольку функция f (x) непрерывна в точке x₀, то существует предел , равный f (x ₀), и так как f (x ₀) > A, то > A. По теореме о сохранении знака для пределов существует проколотая окрестность (x ₀,d), для каждой точки x из которой справедливо неравенство f (x) > A. Добавив к этой окрестности точку x ₀, получим искомую окрестность: U (x ₀,d) = (x ₀,d) È { x ₀}. Теорема доказана.

Замечание. Если f (x ₀) < A, то существует окрестность U (x ₀,d), для любой точки x из которой справедливо неравенство f (x) < A. Докажите самостоятельно.