ТЕОРЕМА 1. Единственность предела.
Если функция f (x) имеет в точке а конечный предел, то только один.
ДОКАЗАТЕЛЬСТВО.
Доказательство теоремы проведем для случая, когда а — конечное число. Предположим, что функция f (x) имеет в точке a два различных конечных предела: 
= А и = В, A ≠ B. Пусть А < B. Возьмем окрестности U (A, e) и U (B, e) точек A и B радиуса 
. Поскольку = А и = В, то
$ 
(a, d1): (x Î (a, d1) Þ f (x) Î U (A, e)) и
$ (a, d2): (x Î (a, d2) Þ f (x) Î U (B, e)).
Возьмем число d = min {d1, d2}. Так как (a, d1) и (a, d2) являются окрестностями одной и той же точки а, то окрестность (a, d) совпадает с меньшей из них и содержится в большей. Следовательно, для х из этой окрестности выполняются оба условия: f (x) Î U (A, e) и f (x) Î U (B, e), то есть
Из последней системы следует, что 
и 
одновременно, что невозможно. Получили противоречие, следовательно, A = B. Теорема доказана. Для случаев a = ±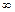 
теорема доказывается аналогично.
ТЕОРЕМА 2. Предел константы.
Если f (x) = C для любого x из некоторой проколотой окрестности (a, d) точки a, то = C.
ДОКАЗАТЕЛЬСТВО.
Возьмем произвольное e > 0. Поскольку для любого x из (a, d) имеем 
, то есть f (x) Î U (C, e), то = C. Теорема доказана.
ТЕОРЕМА 3. Арифметические свойства пределов.
Пусть функции f (x) и g (x) имеют в точке a конечные пределы A и B. Тогда в точке a существуют конечные пределы функций f (x) ± g (x), f (x) · g (x) и 
(при B ≠ 0), причем 
= A ± B, 
= A · B, 
.
ДОКАЗАТЕЛЬСТВО.
Докажем теорему для суммы функций в случае, когда а — конечное число.
Возьмем произвольное e > 0. Поскольку = А, то существует проколотая окрестность (a, d1), для каждой точки х из которой справедливо неравенство
| f (x) – A | < e/2. Поскольку 
= В, то существует проколотая окрестность (a, d2), для каждой точки х из которой справедливо неравенство | g (x) – B | < e/2. Возьмем d = min {d1, d2}. Тогда окрестность (a, d) совпадает с меньшей из окрестностей (a, d1) и (a, d2), и, следовательно, для точек этой окрестности справедливы оба из указанных неравенств. В результате для любого х из (a, d) имеем | f (x) + g (x) – (A + B) | = | ( f (x) – A)+ (g (x) – B) | £ | ( f (x) – A) | + | (g (x) – B) | < e/2 + e/2 = e. Следовательно + g (x) = A + B. Доказательство теоремы для суммы функций закончено. Остальные утверждения теоремы примем без доказательства.
ТЕОРЕМА 4. Об ограниченности функции, имеющей конечный предел.
Если функция f (x) имеет в точке а конечный предел 
= А, то существует проколотая окрестность точки а, в которой функция f (x) ограничена.
ДОКАЗАТЕЛЬСТВО.
Возьмем произвольное e > 0. Поскольку = А, то существует проколотая окрестность (a, d), для каждой точки х из которой справедливо неравенство | f (x) – A | < e. Раскрывая модуль, получим – e < f (x) – A < e, A – e < f (x) < A + e. Справедливость последнего неравенства означает ограниченность функции f (x) в окрестности (a, d). Теорема доказана.
ТЕОРЕМА 5. О сохранении знака.
Пусть = A > B. Тогда существует проколотая окрестность (a, d) точки a, для любой точки x из которой справедливо неравенство f (x) > B.
ДОКАЗАТЕЛЬСТВО.
Возьмем e 
. Согласно определению предела для этого e существует проколотая окрестность (a, d) точки a, для любой точки x из которой справедливо неравенство 
, которое равносильно неравенствам
, 
,
, 
.
Из последнего неравенства следует, что , а так как A > B, то 
. Получили, что для любой точки x из проколотой окрестности (a, d) точки a справедливо неравенство f (x) > B. Теорема доказана.
Замечание. Если = A < B, то существует проколотая окрестность (a, d) точки a, для любой точки x из которой справедливо неравенство f (x) < B. Докажите самостоятельно.
ТЕОРЕМА 6. О предельном переходе в равенстве и неравенстве.
Пусть в некоторой проколотой окрестности (a, d) точки a функции f (x) и g (x) определены и существуют пределы и .
Тогда если для любого x из (a, d) f (x) = g (x), то = ,
если для любого x из (a, d) f (x) £ g (x) или f (x) < g (x), то £ 
.
Без доказательства.
ТЕОРЕМА 7. Принцип сжатой переменной.
Пусть в некоторой проколотой окрестности (a, d0) точки a функции f (x), g (x) и h (x) определены, и для любого x из (a, d0) справедливо неравенство f (x) £ h (x) £ g (x). Тогда если в точке a существуют равные между собой пределы = = A, то существует 
= A.
ДОКАЗАТЕЛЬСТВО.
Доказательство рассмотрим для случая конечной точки а.
Возьмем произвольное e > 0. Поскольку = А и = A, то существует проколотая окрестность (a, d1), для любой точки x из которой справедливо неравенство | f (x) – A | < e, и существует проколотая окрестность (a, d2), для любой точки x из которой справедливо неравенство | g (x) – A | < e. Возьмем d = min {d0, d1, d2}. Тогда окрестность (a, d) совпадает с меньшей из окрестностей (a, d0), (a, d1) и (a, d2), и, следовательно, для точек этой окрестности справедливы три неравенства: f (x) £ h (x) £ g (x), | f (x) – A | < e, | g (x) – A | < e, то есть
f (x) £ h (x) £ g (x), A – e < f (x) < A + e и A – e < g (x) < A + e. Отсюда следует, что для всех х из (a, d) справедливы неравенства A – e < f (x) £ h (x) £ g (x) < A + e, то есть A – e < h (x) < A + e, или | h (x) – A | < e. Значит, 
= A. Теорема доказана.
ТЕОРЕМА 8. О пределе монотонной функции.
Пусть функция f (x) определена и монотонно возрастает на промежутке [a; +¥). Тогда существует предел 
конечный, если f (x) ограничена сверху, и бесконечный, равный +¥, в противном случае. Без доказательства.
БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ
