Пусть функции f (x) и g (x) имеют в точке a конечные или бесконечные пределы. Если эти пределы — конечные числа, то пределы от суммы, разности, произведения и частного этих функций вычисляются согласно теореме об арифметических свойствах пределов. Если предел f (x) — конечное число A, а  = ± ¥, то
= ± ¥, то  + g (x)) = [ A + (± ¥)] = ± ¥,
+ g (x)) = [ A + (± ¥)] = ± ¥,  – g (x)) = [ A – (± ¥)] = K ¥,
– g (x)) = [ A – (± ¥)] = K ¥,
 =
= 
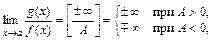 Если предел f (x) — конечное число A, а
Если предел f (x) — конечное число A, а  = ± ¥ или
= ± ¥ или  = 0, то пределы
= 0, то пределы
от частного этих функций вычисляются согласно теореме о связи между бесконечно малыми и бесконечно большими функциями:
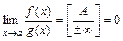 ,
, 

Вопрос о значении предела остается невыясненным в случаях
 – g (x)) = [¥ – ¥],
– g (x)) = [¥ – ¥],  =[0·¥],
=[0·¥],  ,
,  .
.
Такие выражения называются неопределенностями, значения пределов в этих случаях зависят от конкретного вида функций f (x) и g (x). Например,
1)  ;
;
2)  В этих примерах при раскрытии одной и той же неопределенности [¥ – ¥] получили разные ответы.
В этих примерах при раскрытии одной и той же неопределенности [¥ – ¥] получили разные ответы.
В качестве упражнения придумайте примеры, показывающие, что выражения [0·¥],  ,
,  действительно являются неопределенностями.
действительно являются неопределенностями.
При вычислении пределов от функций вида 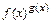 обычно следует перейти к степени с основанием e, воспользовавшись основным логарифмическим тождеством:
обычно следует перейти к степени с основанием e, воспользовавшись основным логарифмическим тождеством: 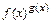 =
=  . Поскольку величина предела такой функции зависит от величины предела
. Поскольку величина предела такой функции зависит от величины предела 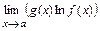 , а при вычислении предела от произведения функций неопределенность возникает только в виде [0·¥], то в нашем случае неопределенность возникнет, если
, а при вычислении предела от произведения функций неопределенность возникает только в виде [0·¥], то в нашем случае неопределенность возникнет, если
1) 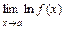 = 0,
= 0,  = ±¥ или 2)
= ±¥ или 2) 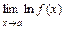 = ±¥,
= ±¥,  = 0.
= 0.
Заметим, что 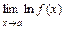 = 0, если
= 0, если  = 1,
= 1, 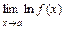 = +¥, если
= +¥, если  = +¥, а
= +¥, а 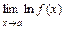 = – ¥, если
= – ¥, если  = 0.
= 0.
Таким образом, получаем неопределенности, возникающие при вычислении пределов от степеней с переменными основанием и показателем: [1¥], [00], [¥0].
В литературе по математическому анализу обычно рассматриваются два предела, получившие названия «первый замечательный предел» и «второй замечательный предел».
Первый замечательный предел  раскрывает неопределенность
раскрывает неопределенность
 и может быть записан еще в трех видах:
и может быть записан еще в трех видах:
 ,
,  ,
,  .
.
Второй замечательный предел  = e раскрывает неопределенность [1¥] и может быть записан еще в трех видах:
= e раскрывает неопределенность [1¥] и может быть записан еще в трех видах: 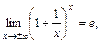
 ,
,  . В последних двух модификациях второго замечательного предела раскрываются неопределенности
. В последних двух модификациях второго замечательного предела раскрываются неопределенности  .
.
Доказательства замечательных пределов можно найти в учебнике Шипачева В.С. (глава 4, § 4).
4. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ С ПОМОЩЬЮ ЭКВИВАЛЕНТНЫХ БЕСКОНЕЧНО МАЛЫХ
ТЕОРЕМА. Пусть функции f (x), f 1(x), g (x), g 1(x) являются бесконечно малыми при стремлении x к a, причем f (x) ~ f 1(x), g (x) ~ g 1(x). Тогда если существует предел  , то существует и предел
, то существует и предел  , причем
, причем  =
= 
ДОКАЗАТЕЛЬСТВО.
Согласно определению эквивалентных бесконечно малых функций  и
и  . Следовательно,
. Следовательно,
 =
= 
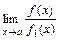 ·
·  ·
·  =
=
= 1·  · 1 =
· 1 =  . Теорема доказана.
. Теорема доказана.
Заметим, что во всех видах записи замечательных пределов, раскрывающих неопределенности  , числитель и знаменатель дроби являются эквивалентными бесконечно малыми. Более того, если a(x) является бесконечно малой при стремлении x к a, то, заменив в этих пределах x на a(x), получим верные равенства, то есть
, числитель и знаменатель дроби являются эквивалентными бесконечно малыми. Более того, если a(x) является бесконечно малой при стремлении x к a, то, заменив в этих пределах x на a(x), получим верные равенства, то есть
 и т. д. Следовательно, если a(x) — бесконечно малая при стремлении x к a, то
и т. д. Следовательно, если a(x) — бесконечно малая при стремлении x к a, то
sin a(x) ~ a(x), tg a(x) ~ a(x), arcsin a(x) ~ a(x), arctg a(x) ~ a(x),
ln (1+a(x)) ~ a(x), e a(x) – 1 ~ a(x).
Приведем несколько примеров на использование эквивалентных бесконечно малых при вычислении пределов.
Пример 1.
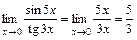 .
.
Здесь использованы эквивалентности бесконечно малых при стремлении x к 0: sin 5 x ~ 5 x и tg 3 x ~ 3 x и применена теорема об эквивалентных бесконечно малых.
Пример 2.
 .
.
Здесь использованы эквивалентности бесконечно малых при стремлении x к 3: ln (1+ x – 3) ~ x – 3 и tg 2(x – 3) ~ 2(x – 3) и применена теорема об эквивалентных бесконечно малых.
НЕПРЕРЫВНОСТЬ ФУНКЦИЙ






