Глава 4. Элементы теории поля
Скалярные и векторные поля.
Поверхность уровня. Векторные линии
Скалярное поле
Функция U(r) 
, где r = 
i 
j 
k – радиус-вектор произвольной точки пространства 
, называется скалярным полем.
Наряду с определенным выше скалярным полем рассматривают плоское скалярное поле, т. е. функцию U(r) 
, где r = i j – радиус-вектор произвольной точки плоскости.
Поверхностью уровня скалярного поля U(r) называется множество точек пространства , удовлетворяющих уравнению 
, где с – произвольная постоянная.
Аналогично определяется понятие линии уровня плоского скалярного поля U(r) .
Векторное поле
Вектор-функция F (r) 
i 
j 
k называется векторным полем.
Вектор-функция F (r) 
i 
j называется плоским векторным полем.
Линии r 
, касательные к которым в каждой точке их совпадают с направлением векторного поля F 
, называются векторными линиями этого поля.
Аналогичным образом определяется понятие векторных линий плоского векторного поля.
Градиент
Градиентом скалярного поля 
называется векторное поле grad 
i 
j 
k 
i 
j 
k.
Градиент скалярного поля в каждой точке перпендикулярен поверхностям уровня этого скалярного поля. Кроме того, градиент скалярного поля 
показывает направление наибольшего роста функции .
Величиной градиента называют скалярное поле
| grad | 
Пример. Найти величину и направление градиента скалярного поля 
в точке 
.
Находим частные производные функции :
, 
, 
.
Таким образом, grad 
i 
j 
k. Подставляя в последнее равенство координаты точки А, получим:
grad 
i – j 
.
Величина градиента при этом будет
| grad 
| 
.
Контрольные вопросы:
- Дайте определение скалярного поля.
- Что называется поверхностью уровня скалярного поля
? - Дайте определение векторного поля.
- Что называют векторными линиями поля F ?
- Дайте определение градиента скалярного поля .
Дивергенция и ротор векторного поля. Оператор Гамильтона
Дивергенция и ротор
Дивергенцией векторного поля F называется скалярное поле, определяемое равенством
div F 
.
Ротором векторного поля F называется векторное поле, определяемое следующим образом:
rot F 
.
Для удобства запоминания принята формальная запись:
rot F 
,
где «умножение» символов дифференцирования на одну из функций понимается как взятие соответствующей частной производной зтой функции.
Физический смысл ротора: если вектор-функция v является полем скоростей твердого тела, вращающегося вокруг неподвижной точки, то с точностью до числового множителя ротор векторного поля v представляет собой мгновенную угловую скорость w этого вращения: w 
rot v.
Ротор векторного поля называют иногда вихрем векторного поля.
Оператор Гамильтона
Оператор Гамильтона или оператор 
(набла) определяется формулой
i 
j 
k.
Применение этого оператора к скалярным и векторным полям с формальной точки зрения соответствует операции «умножения» на вектор с координатами 
:
i j k,
F 
,
F 
.
Нетрудно заметить, что стоящие в правых частях последних трех равенств выражения суть градиент, дивергенция и ротор полей:
grad , F 
div F, F rot F.
Пример. Вычислить дивергенцию и ротор векторного поля
F 
i 
j 
k.
По определению, div F 
. В нашем случае 
, 
, 
. Отсюда находим 
, 
, 
. Следовательно,
div F 
.
Вычислим ротор поля F:
rot F 
i 
j 
k 
i 
j
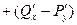k 
.
Контрольные вопросы:
- Дайте определение дивергенции векторного поля F .
- Дайте определение ротора векторного поля F .
- Какой формулой определяется оператор Гамильтона?
Поток векторного поля
Пусть в области 
задано некоторое векторное поле F 
i 
j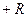 
k, где 
, 
, 
– непрерывно дифференцируемые в области 
функции. Пусть 
– гладкая ориентируемая поверхность, на которой выбрана определенная сторона, задаваемая единичной нормалью n 
к этой поверхности.
Потоком векторного поля F через поверхность S в направлении единичной нормали n называют поверхностный интеграл первого рода:
П  .
| (1) |
Поверхностный интеграл первого рода в формуле (1) связан с поверхностным интегралом второго рода равенством:
П  ,
| (2) |
которое дает еще один способ вычисления потока.
Физический смысл потока: если вектор-функция F есть поле скоростей текущей жидкости, то поток П этого векторного поля через поверхность S общему количеству жидкости, протекающей через S за единицу времени.
