Хвильові процеси
У середовищі частинки зв’язані між собою силами взаємодії. Періодичне невелике зміщення деякої частинки середовища з положення рівноваги викликає зміщення сусідніх частино, тобто коливання одної з таких частинок викликає вимушені коливання інших. Процес розповсюдження коливань в середовищі із деякою швидкістю V називається хвилею. Якщо зміщення частинок x від положення рівноваги перпендикулярне швидкості V, то така хвиля називається поперечною,а якщо x паралельне V ¾ хвиля повздовжня. Швидкість хвилізалежить від сили взаємодії між частинками середовища - чим більша сила взаємодії, тим більша швидкість хвилі. Для твердого тіла
V=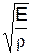 
,
де Е ¾ модуль Юнга, r ¾ густина речовини. Для повітря (газу)
V=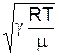 
= 
,
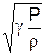де g ¾ стала адіабати, R ¾ універсальна газова стала, Т ¾ температура, m ¾ маса моля речовини, r ¾ густина повітря (газу), Р ¾ тиск газу.
Наведемо деякі визначення характеристик хвильового процесу.
1. Хвильовий фронт¾ геометричне місце точок середовища, до яких дійшли коливання.
2. Плоскою називається хвиля, у якої хвильовий фронт є нескінченною площиною.
3. Сферичною називається хвиля, у якої хвильовий фронт є сферою.
4. Циліндричною називається хвиля, у якої хвильовий фронт обмежений скінченою площиною.
5. Промінь¾ уявна крива, дотична до якої визначає напрямок розповсюдження коливань.
Рівняння хвилі, фаза та фазова швидкість
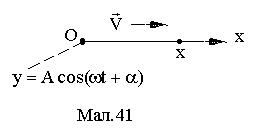Рівняння хвилі, що розповсюджується в додатному напрямкові Ох, описує величину відхилення y матеріальної точки від положення рівноваги, з координатою х в момент часу t і має вигляд
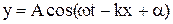. (1)
Дійсно, нехай джерело коливань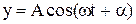 
розміщено в початку координат, і коливання розповсюджуються в додатному напрямкові осі ОХ із швидкістю 
(див.Ма.41). В точку з координатою х коливання прийдуть із запізненням на час розповсюдження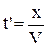 
, і тому рівняння коливання в цій точці в час t запишеться так
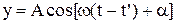(2)
або
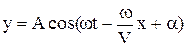. (3)
Остаточно рівняння хвилізапишеться у вигляді
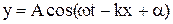, (4)
де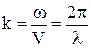 
¾ хвильове число.
В (4) косинус є періодичною функцією з періодом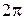 
, а тому можна визначити її період 
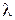по координаті х
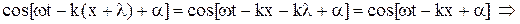
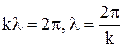. (5)
За визначенням довжина хвилі¾ відстань, на яку поширюється хвиля за період коливань Т: l=VT. З (4) видно, що довжина хвилі 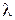є періодом просторового розподілу коливань частинок середовища.
Якщо коливання розповсюджуються в зворотному напрямі, то х замінюємо на -х і рівняння зворотної хвилімає вигляд
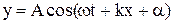. (6)
Величина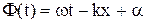 
в (4) називається фазою хвилі,а 
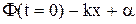- початкова фаза. Зафіксуємо величину фази на рівні сталої С
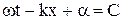. (7)
Візьмемо диференціал від лівої та правої частини (7)
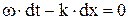. (8)
З (8) можна визначити величину
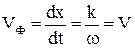, (9)
яка називається швидкістюрозповсюдження фази коливань або фазовою швидкістю і вона за величиною дорівнює швидкості хвилі.
Плоска хвиля
Рівняння плоскої хвилі має вигляд:
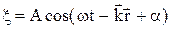, (1)
де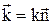 
¾ хвильовий вектор, 
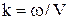¾ хвильове число, 
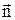¾ одиничний вектор нормалі до хвильового фронту.
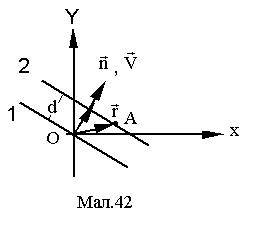
Дійсно, нехай джерелом коливань є нескінченно велика площина 1 (див. Мал. 42) із нормаллю 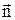, що є хвильовим фронтом плоскої хвилі. Площина проходить через початок координат. Нехай рівняння коливання точок в площині 1 має вигляд
x=Acos(wt+a). (2)
Через час t' площина 1 переміститься на відстань d і займе положення 2. Відстань між площинами визначається скалярним добутком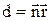 
, де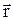 
¾ радіус-вектор деякої точки А на площині. Коливання в цій площині запізнюються на час 
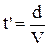і будуть мати вигляд
x = Acos(wt - wt' + a) = Acos(wt - w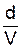 
+ a) = Acos(wt - kd + a). (3)
Тепер, позначивши 
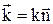, можна записати:
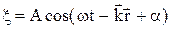, (4)
що й треба було довести.
Сферична хвиля. Рівняння сферичної хвилімає вигляд
y=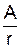 
cos(wt-kr). (5)
Амплітуда сферичної хвилі зменшується обернено пропорційно відстані r від джерела хвиль, а енергія обернено пропорційна квадратові відстані.
Циліндрична хвиля. Циліндрична хвиля описується рівнянням плоскої хвилі з обмеженим деякою плоскою поверхнею хвильовим фронтом.
 |
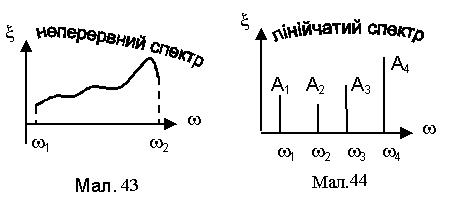Спектр частот хвиль. Під частотним спектром хвилірозуміють сукупність частот, якими можна представити дану хвилю.
Хвиля з неперервним спектром частот ¾ хвиля, що містить значення частоти коливань в деякому неперервному інтервалі частот від w1 до w2 (див. Мал.43).
Хвиля з лінійчатим спектромчастот ¾ хвиля, що містить коливання дискретних значень частоти (див. Мал.44).
