Дана прямая 
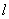, которая пересекает оси координат и не параллельна ни одной из них. Пусть угол наклона к положительному направлению оси Ox равен 
. Угол отсчитывается от Ox против часовой стрелки 
– угол наклона прямой 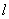к положительному направлению оси Ox. Точка пересечения с Oy – 
.
Пусть 
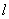– произвольная точка . Рассмотрим 
. Он прямоугольный и имеет острый угол . 
Найдем 
(отношение противолежащего катета к прилежащему).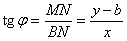 
Обозначим через 
. Имеем: 
или 
, 
– уравнение прямой с угловым коэффициентом.
Частные случаи:
1) 
, 
– уравнение прямой, параллельной оси Ох и отстоящей от нее на 
;
2) 
, 
– прямая проходит через начало координат;
3) 
, 
– уравнение оси Ox;
4) 
– уравнение прямой, параллельной оси Oy и отстоящей от нее на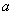 
;
5) 
– уравнение оси Oy;
6) 
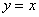– уравнение биссектрисы I и III координатных углов;
7) 
– уравнение биссектрисы II и IV координатных углов.
Общее уравнение прямой:
где A, B и C – коэффициенты, одновременно не равные нулю.
В зависимости от значений постоянных А, В и С возможны следующие частные случаи:
C = 0, – прямая проходит через начало координат
А = 0, {By + C = 0} - прямая параллельна оси Ох
В = 0, {Ax + C = 0} – прямая параллельна оси Оу
В = С = 0, – прямая совпадает с осью Оу
А = С = 0, – прямая совпадает с осью Ох
Расстояние от точки до прямой:
Доказательство. Пусть точка М1(х1, у1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1:
(1)
Координаты x1 и у1 могут быть найдены как решение системы уравнений:
Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М0 перпендикулярно заданной прямой.
Если преобразовать первое уравнение системы к виду:
A(x – x0) + B(y – y0) + Ax0 + By0 + C = 0,
то, решая, получим:
Подставляя эти выражения в уравнение (1), находим:
где 
- угол, образуемый нормально к прямой и осью Ox; p - расстояние от начала координат до прямой.
Уравнение прямой в отрезках на плоскости в прямоугольной системе координат Oxy имеет вид 
, где a и b - некоторые отличные от нуля действительные числа.
Векторно-параметрическое уравнение прямой:
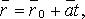
где 
- фиксированная точка, лежащая на прямой; 
- направляющий вектор (см. рис. 4.11).
В координатах (параметрические уравнения):
Уравнение прямой, проходящей через две данные (различные) точки 
и 
Билет №5(2)
Взаимное расположение прямых на плоскости:
· Две прямые на плоскости могут совпадать.
Это возможно в том случае, когда прямые имеют по крайней мере две общие точки. Действительно, в силу аксиомы, озвученной в предыдущем пункте, через две точки проходит единственная прямая. Иными словами, если через две заданные точки проходят две прямые, то они совпадают.
· Две прямые на плоскости могут пересекаться.
В этом случае прямые имеют одну общую точку, которую называют точкой пересечения прямых. Пересечение прямых обозначают символом «
», к примеру, запись 
означает, что прямые а и b пересекаются в точке М. Пересекающиеся прямые приводят нас к понятию угла между пересекающимися прямыми. Отдельно стоит рассмотреть расположение прямых на плоскости, когда угол между ними равен девяноста градусам. В этом случае прямые называются перпендикулярными (рекомендуем статью перпендикулярные прямые, перпендикулярность прямых). Если прямая a перпендикулярна прямой b, то можно использовать краткую запись 
.
· Две прямые на плоскости могут быть параллельными, если они не имеют общих точек. Если прямая a параллельна прямой b, то используют символическое обозначение 
.
Две прямые называются коллинеарными, если они параллельны или совпадают.
Прямые параллельны тогда и только тогда, когда соответствующие коэффициенты при неизвестных в их уравнениях пропорциональны, т.е. существует такое число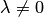 
, что 
, но 
. Прямые совпадают тогда и только тогда, когда все соответствующие коэффициенты в их уравнениях пропорциональны:
Взаимное расположение прямой и плоскости:
Рассмотрим плоскость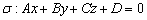 
и прямую 
, заданную точкой 
и направляющим вектором 
.
Существует три варианта взаимного расположения прямой и плоскости:
1. прямая пересекает плоскость в некоторой точке 
;
2. прямая параллельна плоскости: 
;
3. прямая лежит в плоскости: 
.
Аналитические условия:
Прямая пересекает плоскость тогда и только тогда, когда её направляющий вектор 
не ортогонален вектору нормали 
плоскости.
Из утверждения следует, что скалярное произведение вектора нормали и направляющего вектора будет отлично от нуля: 
.
Если же данные векторы ортогональны, то есть если их скалярное произведение равно нулю: 
, то прямая либо параллельна плоскости, либо лежит в ней:
· Если прямая параллельна плоскости, то точка (а, значит, и ЛЮБАЯ точка данной прямой) не удовлетворяет уравнению плоскости: 
.
· 
Если прямая лежит в плоскости, то точка 
(а, значит, и ЛЮБАЯ точка данной прямой) удовлетворяет уравнению плоскости: 
.
Угол между прямой и плоскостью:
